BUAA OO第一次作业总结
简介:
第一单元的作业的主要任务为解析一个包含加、减、乘、乘方以及括号的表达式,其最终任务是处理一个括号可嵌套并含有自定义函数以及求和函数的表达式。
由于三次作业中采用的是增量开发而并未重构,故只展示第三次作业的复杂度分析和UML图,并借此阐述设计思路和架构。
UML图与类结构
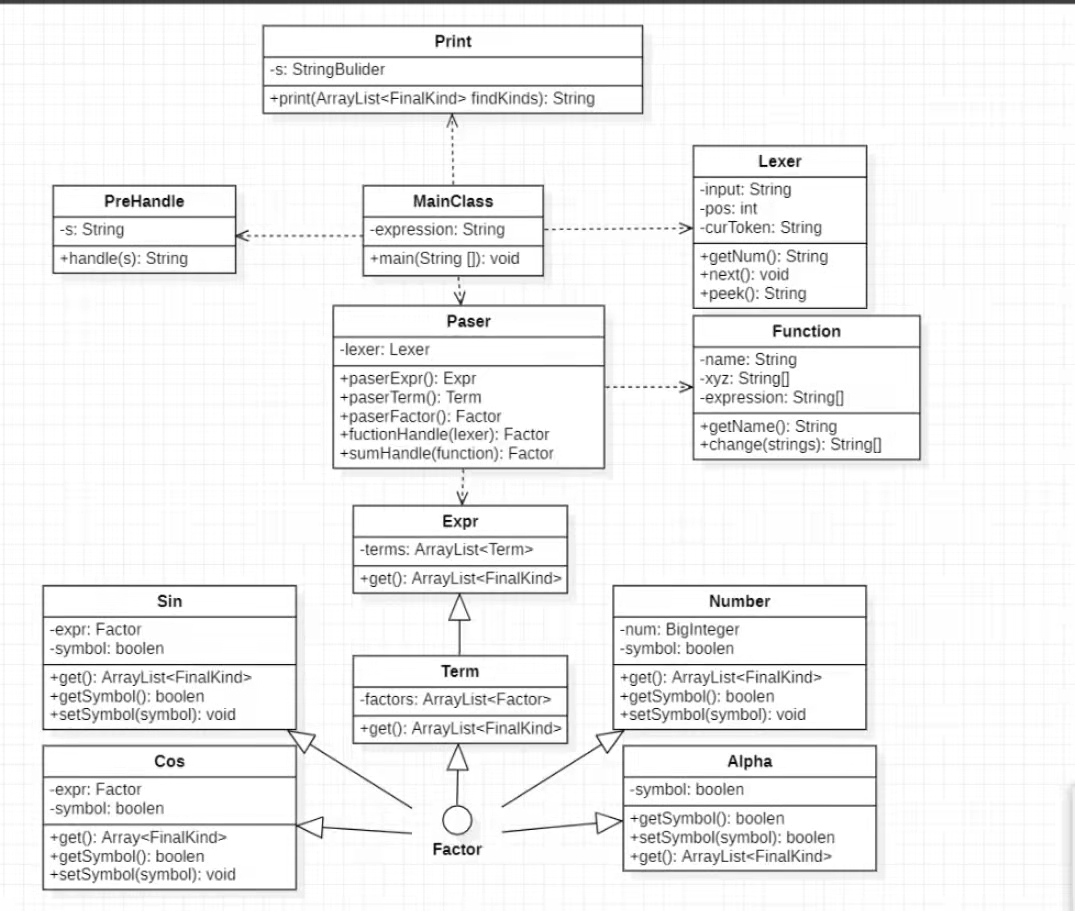
主要的类的解释:
MainClass:主函数,其主要作用是调用其他函数
Print:最后的输出函数,输出最后的表达式。
PeHandle:预处理作用,将输入的字符串进行预处理,除去其中的空白字符,不必要的加减号,以及将**展开。
Factor:作为各种因子的接口。
Sin,Cos,Num,Alpha:为具体因子的实现。
Term:是Factor的集合。
Expr:Term的集合。
Lexer:对表达式进行文法分析。其具体方式是将字符串逐个字符的分析并返回给Parser类。
Parser:利用lexer分析的结构来确定该字符按何种方式进行提取和处理,具体方法有parserExpr、 paserTerm 以及 parserFactor。
Function: 函数类,储存了自定义函数的变元(x,y,z), 函数的名称(f,g,h),以及函数的定义。
复杂度分析
仅展示了复杂度相对较高的方法
| method | CogC | ec(G) | iv(G) | v(G) |
| Function.changeExpression(String[]) | 2.0 | 1.0 | 2.0 | 3.0 |
| Lexer.getNumber() | 2.0 | 1.0 | 3.0 | 3.0 |
| Lexer.next() | 3.0 | 2.0 | 2.0 | 3.0 |
| MainClass.main(String[]) | 6.0 | 1.0 | 5.0 | 5.0 |
| Mul.mul(ArrayList, ArrayList) | 15.0 | 1.0 | 7.0 | 7.0 |
| No.no(ArrayList) | 1.0 | 1.0 | 2.0 | 2.0 |
| Parser.functionHandle(Lexer) | 16.0 | 1.0 | 7.0 | 11.0 |
| Parser.parseExpr() | 1.0 | 1.0 | 2.0 | 2.0 |
| Parser.parseFactor() | 12.0 | 8.0 | 10.0 | 10.0 |
| Parser.parseTerm() | 1.0 | 1.0 | 2.0 | 2.0 |
| Parser.sumHandle(Lexer, ArrayList) | 10.0 | 2.0 | 4.0 | 7.0 |
| PreHandle1.handle(String) | 34.0 | 1.0 | 23.0 | 25.0 |
| PreHandle2.handle(String) | 52.0 | 1.0 | 18.0 | 21.0 |
| Print.handlePrint(FinalKind, StringBuilder) | 15.0 | 1.0 | 9.0 | 9.0 |
| Print.print(ArrayList) | 10.0 | 1.0 | 5.0 | 7.0 |
| Print.scPrint(FinalKind, StringBuilder) | 9.0 | 1.0 | 7.0 | 7.0 |
| Term.get() | 8.0 | 1.0 | 5.0 | 7.0 |
设计思路
第一次接触这个问题时,我并没有什么思路,主要是在阅读完课程组提供的文件中一个对后缀表达式解析的程序之后,我才逐渐有了递归下降法的思维,并尝试着用它去解决问题。在做题的过程中我不断理解递归下降法的含义。首先表达式通过正负号的分隔,递归下降成项。而项又可以通过*的分隔,递归下降成因子处理,因子中又包含了常规因子和表达式因子。常规因子例如sin cos x 以及常数,这些都可以直接解析出结构。但是另一种特殊的因子,表达式因子,则不能直接解析得到。但是其又可以通过调用对表达式的解析,从而形成一个优美的递归结构,对表达式解析层层解析。
架构优缺点分析
优点:采用了递归下降法的分析方式,使得程序的可扩展性较强,三次作业中并未进行重构。
缺点:由复杂度分析可以看到,在我的方法中有较多的方法复杂度较高,这说明了我设计上的极大的不足与缺陷,其原因主要是在字符串解析之前,我将字符串进行了预处理,将不必要的加减号以及空格除去,并且将**展开为。而预处理环节需要采用嵌套循环的方式来遍历整个字符串,结构导致预处理的方法中复杂度较高。但其实只要深入去理解题目就会发现,很多预处理是不必要的,可以在递归下降法中很好的并且自然的处理它们,这体现了我对递归下降法的理解还不够深入。同时在Paser类中,我的代码耦合度较高,这也体现了结构化设计的不足,以及对面向对象思维理解的不够深入。
关于化简
在第一次的作业中,大体上,化简只需将同类项合并即可,细节上的优化可以有:
(1)x**2变成x*x
(2)[1/-1]*factors的情况下,将1*省略,当系数为0时,则整项都不输出。
(3)将系数非负的项(如果存在的话)作为表达式的首项。
第二次作业中,则需在第一次的基础上再进行三角函数的化简。化简的一些思路如下。
(1)若sin内的幂函数系数为负,则将负号提出。若cos内的幂函数系数为负,则直接变为正。
(2)将sin(0)化简成0,cos(0)化简成1。
(3)将sin(x)**2+cos(x)**2化简为1.大体思路如下,遍历表达式中的每一项,当找到一项为sin时,检查它的系数是否大于等于2,若成立,则遍历后面的项,若存在项的cos系数大于等于2且里面存的表 达式与之前的sin相同,则将两项sin的系数和cos的系数分别减二,比较剩余的部分是否为同类项。若是,则合并,若不是,则将两项的系数再重新加二,回到原来的状态。
第三次作业中,由于sin和cos中的存储类发生了变化,导致之前的方法需要一些小小的改动,但由于事件原因,最终没能完成化简。
bug分析
在第一次作业中互测和强测均不存在bug,同时也没有成功hack别人。
在第二次作业中,强测时因为sin(x**2)错误的输出了sin(x*x),导致错了一个点,其余测试点均为满分。互测中没有被测出bug。同时hack了别人一个bug。在类似(+-+2)这种数字前带三个符号的情况下,那位同学的程序会发生一些错误,可能是将正负号提前处理了,但没有处理完全。
在第三次的作业中,强测时因为一个地方复制粘贴时忘了改动,导致在某些特殊情况下会输出格式错误。其余测试点均正确,但由于没有做优化,性能分损失较大。互测中没有被测出bug,同时hack了别人三个bug。首先sum中他没有考虑超大整数的情况和例如i**2的情况。同时他在输出时直接将1*省略。导致例如11*x就只会输出1x。
反思与总结
三次作业过后,可以感觉出相较于之前的进步,对层次化设计和结构化设计有了更深一步的了解,同时也切实感受到了助教和老师们的认真负责,一旦出现问题就立马会全心全意的为我们解答,可以说这门课的高质量学习是完全离不开这些负责的老师和助教的。但是我在设计中还存在很多不足,没有养成一种良好的写代码的风格和习惯,导致很多时候只是想着完成任务,而没有去关注更重要的代码风格和层次架构,希望在之后的几次练习后,我能逐渐的养成这些良好的习惯。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号