环图问题

环图由一些简单的链和环组成。

对于有向图，所有点入度与出度 <= 2，就是一个环图

对于无向图，所有点的度数 <= 2，就是一个环图

环图中所有的链与环互不相交。

常见问题：环的大小，个数，路径

 

 

 

 这种无序变有序的问题，建图方法:把起点向终点连一条边。每个点入度出度都是1，所以建成的图中只存在若干简单环和自环。

目标是将图中的所有环变为n个自环，最少操作 n - m次。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 5e5 + 10;

string str;
int a[N], b[N], idx;

int main() {
    cin >> str;
    
    int n = str.size();
    int s[3] = {0};
    for(int i = 0; i < n; i ++ ) {
        if(str[i] == 'L') a[i] = 0;
        else if(str[i] == 'M') a[i] = 1;
        else a[i] = 2;
        s[a[i]] ++ ;
    }
    
    for(int i = 0; i < 3; i ++ ) {
        for(int j = 0; j < s[i]; j ++ ) {
            b[idx ++ ] = i;
        }
    }
    
    int e[3][3] = {0};
    for(int i = 0; i < n; i ++ ) {
        e[b[i]][a[i]] ++ ; 　　//建图，为若干有向环
    }
    
    int m = 0;
    for(int i = 0; i < 3; i ++ ) {
        m += e[i][i];　　　　//加上自环数量，
    }
    
    for(int i = 0; i < 3; i ++ ) {
        for(int j = i + 1; j < 3; j ++ ) {
            int t = min(e[i][j], e[j][i]);　　//加上小环数量
            m += t, e[i][j] -= t, e[j][i] -= t; //删除小环
        }
    }
    
    m += e[0][1] + e[1][0]; 　//小环删除后只剩下大环，正向或反向
    
    cout << n - m << endl;
    
    return 0;
}

 

与题目一思路相同的一道题：

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010;

int n;
int a[N], b[N], idx;

int main() {
    cin >> n;
    
    int s[4] = {0};
    for(int i = 0; i < n; i ++ ) {
        cin >> a[i];
        s[a[i]] ++ ;
    }
    
    for(int i = 1; i <= 3; i ++ ) {
        for(int j = 0; j < s[i]; j ++ ) {
            b[idx ++ ] = i;
        }
    }
    
    int e[4][4] = {0};
    for(int i = 0; i < n; i ++ ) {
        e[b[i]][a[i]] ++ ;
    }
    
    int m = 0;
    for(int i = 1; i <= 3; i ++ ) m += e[i][i];
    
    for(int i = 1; i <= 3; i ++ ) {
        for(int j = i + 1; j <= 3; j ++ ) {
            int t = min(e[i][j], e[j][i]);
            m += t, e[i][j] -= t, e[j][i] -= t;
        }
    }
    
    m += e[1][2] + e[2][1];
    
    cout << n - m << endl;
    
    return 0;
}

 

 

 

 建图方式：起点向变换点连边。

要求每个点所在环的大小 -> 并查集。

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 2e5 + 10;

int n;
int p[N], s[N], a[N];

int find(int x) {
    if(x != p[x]) p[x] = find(p[x]);
    return p[x];
}

int main() {
    
    int T;
    scanf("%d", &T);
    while(T -- ) {
        scanf("%d", &n);
        for(int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
        for(int i = 1; i <= n; i ++ ) p[i] = i, s[i] = 1;
        
        for(int i = 1; i <= n; i ++ ) {
            int pa = find(i), pb = find(a[i]);
            if(pa != pb) {
                s[pb] += s[pa];
                p[pa] = pb;
            }
        }
        
        for(int i = 1; i <= n; i ++ ) cout << s[find(i)] << ' ';
        cout << endl;
    }
    
    return 0;
}

 

 

建图方式：将每个点分为上半和下半两个点，把能互相连通的点连边。

这一题目有涉及到了方向变化问题，遇到此类问题，我们就将所有方向按顺时针从0开始编号，按题意找规律即可。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010;

int n, m;
char g[N][N];

int dx[] = {-1, 0, 1, 0};
int dy[] = {0, 1, 0, -1};

int dfs(int x, int y, int d) {
    if(x < 0 || x >= n || y < 0 || y >= m) return 0;
    
    if(g[x][y] == '/') d ^= 1;
    else d ^= 3;
    
    return dfs(x + dx[d], y + dy[d], d) + 1;
}

int main() {
    scanf("%d%d", &n, &m);
    
    for(int i = 0; i < n; i ++ ) {
        for(int j = 0; j < m; j ++ ) {
            cin >> g[i][j];
        }
    }
    
    int res = 0;
    for(int i = 0; i < n; i ++ ) {
        res = max(res, dfs(i, 0, 1));
        res = max(res, dfs(i, m - 1, 3));
    }
    
    for(int i = 0; i < m; i ++ ) {
        res = max(res, dfs(0, i, 2));
        res = max(res, dfs(n - 1, i, 0));
    }
    
    cout << res << endl;
    
    return 0;
}

 

 

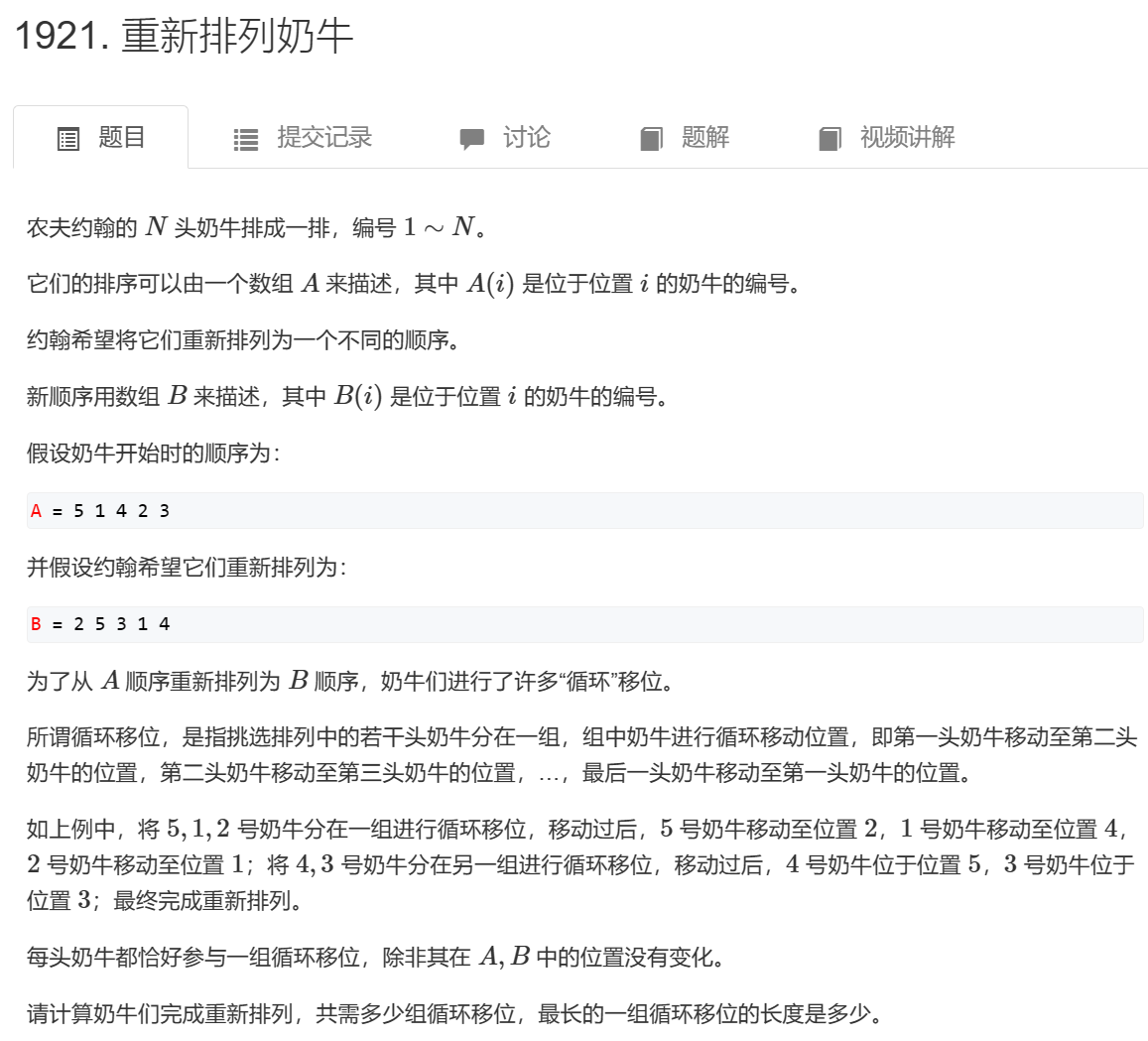
 建图方式:起点向终点连边。

我们要找环的个数和最大环的点数。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 110;

int n;
int a[N], b[N], p[N], s[N];

int find(int x) {
    if(x != p[x]) p[x] = find(p[x]);
    return p[x];
}

int main() {
    cin >> n;
    
    int cnt = 0, sz = -1;
    
    for(int i = 1; i <= n; i ++ ) p[i] = i, s[i] = 1;
    
    for(int i = 1; i <= n; i ++ ) cin >> a[i];
    for(int i = 1; i <= n; i ++ ) cin >> b[i];
    
    
    for(int i = 1; i <= n; i ++ ) {
        int pa = find(a[i]), pb = find(b[i]);
        if(pa != pb) {
            s[pb] += s[pa];
            p[pa] = p[pb];
        }
    }
    
    for(int i = 1; i <= n; i ++ ) {
        if(a[i] == find(a[i]) && a[i] != b[i]) {
            cnt ++ ;
            sz = max(sz, s[a[i]]);
        }
    }
    
    cout << cnt << ' ' << sz << endl;
    
    return 0;
}

 

 

 

 与之前类似的环图构造法，从i 向 f[i]连一条边。本题要求i != f[i]及不能有自环。

对于这种环图，我们可以开关联数组记录每个点的入边和出边，来存图。

对于孤立点，我们可以把它加入任意环。

令p[x]为x的入边，q[x]为x的出边。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 2e5 + 10;

int n;
int p[N], q[N];
bool st[N];

int main() {
    int T;
    cin >> T;
    while(T -- ) {
        memset(p, 0, sizeof p);
        memset(q, 0, sizeof q);
        memset(st, 0, sizeof st);
        
        cin >> n;
        for(int i = 1; i <= n; i ++ ) {
            cin >> p[i];
            q[p[i]] = i;
        }
        
        bool flag = false;
        for(int i = 1; i <= n; i ++ ) {
            if(st[i] || !p[i] && !q[i]) continue;
            st[i] = true;
            int x = i, y = i;
            while(p[x] && !st[p[x]]) x = p[x], st[x] = true;  //寻找环的开始
            while(q[y] && !st[q[y]]) y = q[y], st[y] = true;  //寻找环的结尾
            
            if(p[x] == y) continue;  // 如果已经成环
            
            if(!flag) {
                flag = true;
                for(int j = 1; j <= n; j ++ ) {
                    if(!p[j] && !q[j]) {  //遍历所有点，将孤立点加入环中
                        p[x] = j;
                        x = j;
                        st[x] = true;
                    }
                }
                p[x] = y;
            } else {
                p[x] = y;
            }
        }
        
        if(!flag) {
            int x = 0, y = 0;
            for(int j = 1; j <= n; j ++ ) {
                if(!p[j] && !q[j]) {
                    if(!x) x = y = j;
                    else {
                        p[x] = j;
                        x = j;
                    }
                }
            }
            p[x] = y;
        }
        
        for(int i = 1; i <= n; i ++ ) {
            cout << p[i] << ' ';
        }
        cout << endl;
    }
    
    return 0;
}