地铁最短路径
项目介绍
实现一个推荐地铁最短线路的算法,输入出发点和终点,输出推荐线路
一.主要功能
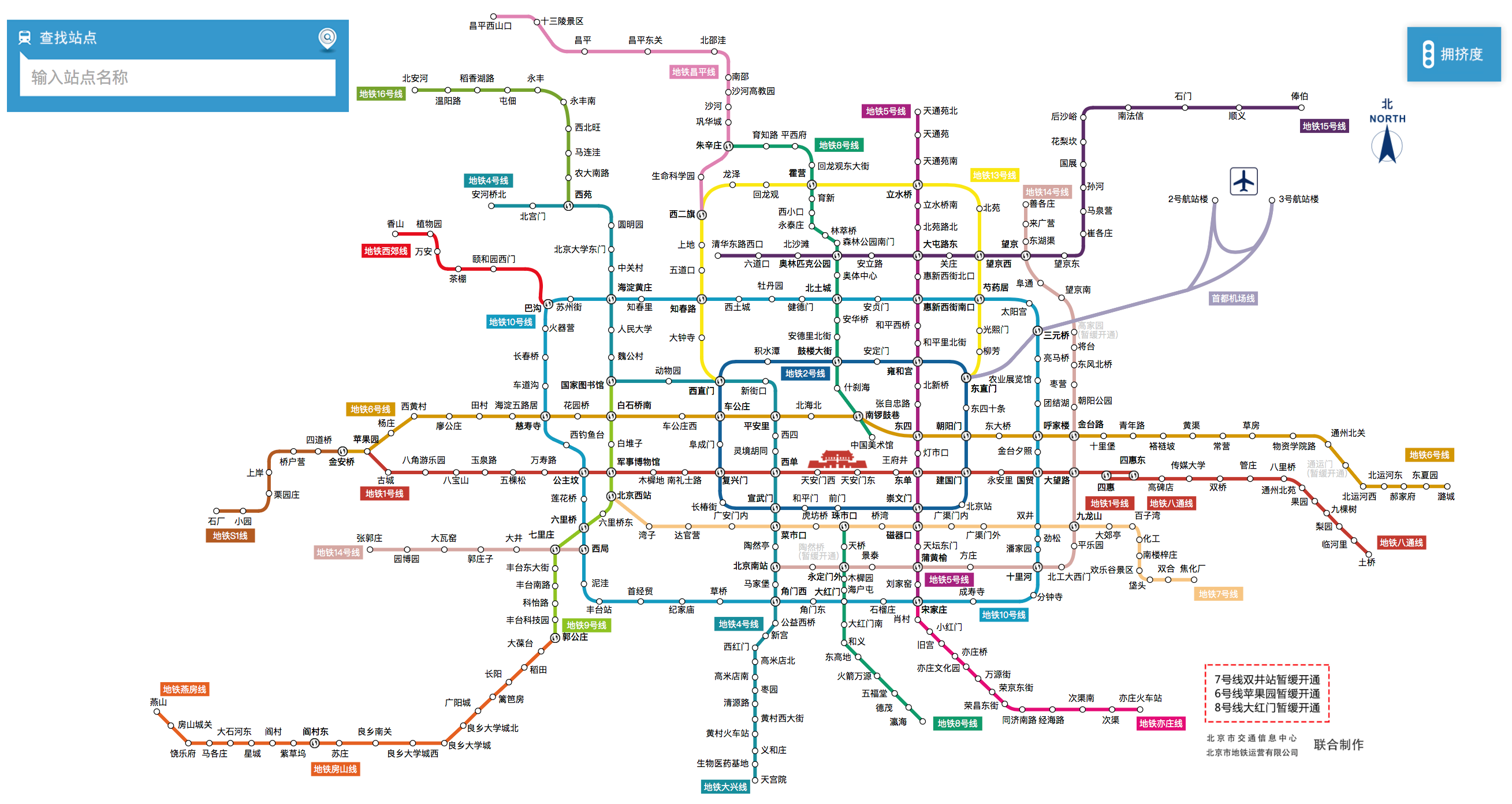
提供一副地铁线路图,计算指定两站之间最短(最少经过站数)乘车路线;输出指定地铁线路的所有站点。以北京地铁为例,地铁线路信息保存在data.txt中,格式如下:
地铁线路总数
线路名1 站名1 站名2 站名3 ...
线路名2 站名1 站名2 站名3 ...
线路名3 站名1 站名2 站名3 ......
二.需求分析
1.能正确读入data.txt文件的内容
2.能够查询某号线路的所有站点信息
3.能输出出发地和目的地之间的推荐出行路径
三.实现语言
java
四.实现算法
dijkstra算法
https://github.com/zjx-github/sub
五.类职责划分
Class Result 用于结果的保存
`private Station startStation; //起始站`
`private Station endStation; //终点站`
`private int distance; //距离`
`private Station lastStations; //所在上一站`
`private String line; //所在线路`
`private int linechange; //是否换乘站`
Class Station 站点信息的保存
`private String stationName; //站点名`
`private List<String> line=new ArrayList<String>(); //所在线路名`
`private List<Station> linkStations = new ArrayList<Station>(); //相邻站点`
Class SubControl 用于地铁功能的实现
`private static Station nextStation()//获取下一个站点`
`private static List<String> getSameLine(List<String> line1,List<String> line2) //获取两条线路的相同`
`public static Result shortestPath(Station start, Station end) //dijkstra算法处理最短路径`
`public static List<Station> getLineStation(String linename) //获取该线路的所有站点`
`public static List<String> getPath(Result r) //生成推荐路线`
Class Subline 用于构造地铁线路集
读入数据生成一个LinkedHashSet
六.核心代码
构造地铁线路
`public static LinkedHashSet<List<Station>> lineSet = new LinkedHashSet<List<Station>>(); //线路集合
public Subline(String path) throws IOException{
File filename = new File(path);
InputStreamReader reader = new InputStreamReader( new FileInputStream(filename));
BufferedReader br = new BufferedReader(reader);
String content="";
content=br.readLine(); //读第一行获取总的线路和
int linenum=Integer.parseInt(content);
for(int i=0;i<linenum;i++) { //构造集合增加线路
content=br.readLine();
List<Station> line=new ArrayList<Station>();
String[] linearr=content.split(" ");
String linename=linearr[0];
for(int j=1;j<linearr.length;j++) { //向线路中添加站点
//System.out.println();
int flag=0;
for(List<Station> l:lineSet) { //处理换乘
for(int k=0;k<l.size();k++) {
if(l.get(k).getstationName().equals(linearr[j])) {
//System.out.println(l.get(k).getLine());
List<String> newline=l.get(k).getLine();
newline.add(linename);
l.get(k).setLine(newline);
line.add(l.get(k));
flag=1;
break;
}
}
if(flag==1)
break;
}
if(j==linearr.length-1&&linearr[j].equals(linearr[1])) { //环线
line.get(0).getLinkStations().add(line.get(line.size()-1));
line.get(line.size()-1).getLinkStations().add(line.get(0));
flag=1;
}
if(flag==0)
line.add(new Station(linearr[j],linename));
}
for(int j=0;j<line.size();j++) { //处理车站相邻车站
List<Station> newlinkStations=line.get(j).getLinkStations();
if(j==0) {
newlinkStations.add(line.get(j+1));
line.get(j).setLinkStations(newlinkStations);
}
else if(j==line.size()-1) {
newlinkStations.add(line.get(j-1));
line.get(j).setLinkStations(newlinkStations);
}
else {
newlinkStations.add(line.get(j+1));
newlinkStations.add(line.get(j-1));
line.get(j).setLinkStations(newlinkStations);
}
}
lineSet.add(line);
//System.out.println(lineSet.size());
}
br.close();
}`
地铁功能的实现
`private static List<Station> visited = new ArrayList<>(); //以访问过站点
private static HashMap<Station, Result> resultset = new HashMap<>();//结果集
private static Station nextStation() {//获取下一个站点
int min=999999;
Station rs = null;
Set<Station> stations = resultset.keySet();
for (Station station : stations) {
if (visited.contains(station)) {
continue;
}
Result result = resultset.get(station);
if (result.getDistance() < min) {
min = result.getDistance();
rs = result.getEndStation();
}
}
return rs;
}
private static List<String> getSameLine(List<String> line1,List<String> line2) { //获取两条线路的相同
List<String> sameline=new ArrayList<String>();
for(String la:line1) {
for(String lb:line2) {
if(la.equals(lb))
sameline.add(la);
}
}
return sameline;
}
public static Result shortestPath(Station start, Station end) {//dijkstra算法处理最短路径
for (List<Station> l:Subline.lineSet) {//构造结果集
for(int i = 0 ; i < l.size(); i++) {
Result re = new Result();
re.setStartStation(start);
re.setEndStation(l.get(i));
re.setDistance(9999);
re.setLinechange(0);
resultset.put(l.get(i), re);
}
}
for(Station s:start.getLinkStations()) { //初始化
resultset.get(s).setDistance(1);
resultset.get(s).setLastStations(start);
List<String> samelines=getSameLine(start.getLine(),s.getLine());
resultset.get(s).setLine(samelines.get(0));
}
resultset.get(start).setDistance(0);
visited.add(start);
Station ns = nextStation();//获取下一站点
while(ns!=null) {
for(Station s:ns.getLinkStations()) {
if(resultset.get(ns).getDistance()+1<resultset.get(s).getDistance()) {
resultset.get(s).setDistance(resultset.get(ns).getDistance()+1);
resultset.get(s).setLastStations(ns);
List<String> samelines=getSameLine(ns.getLine(),s.getLine());
if(!samelines.contains(resultset.get(ns).getLine())) {
resultset.get(s).setLine(samelines.get(0));
resultset.get(s).setLinechange(1);
}
else {
resultset.get(s).setLine(resultset.get(ns).getLine());
}
}
}
visited.add(ns);
ns = nextStation();
}
return resultset.get(end);
}
public static List<Station> getLineStation(String linename){ //获取该线路的所有站点
int flag=1;
List<Station> temp = new ArrayList<Station>();
for (List<Station> l:Subline.lineSet) {
flag=1;
for(Station s :l) {
if(!s.getLine().contains(linename)) {
flag=0;
//System.out.println(s.getstationName());
}
else {
temp.add(s);
}
}
if(flag==1)
return l;
}
return temp;
}
public static List<String> getPath(Result r){ //生成推荐路线
List<String> path=new ArrayList<String>();
Stack<Station> tmp=new Stack<Station>();
Station s=r.getLastStations();
while(!s.equals(r.getStartStation())) {
tmp.push(s);
s=resultset.get(s).getLastStations();
}
path.add(r.getStartStation().getstationName());
while(!tmp.empty()) {
if(resultset.get(tmp.peek()).getLinechange()==1) {
path.add("->换乘"+resultset.get(tmp.peek()).getLine());
path.add(tmp.pop().getstationName());
}
else
path.add(tmp.pop().getstationName());
}
if(r.getLinechange()==1) {
path.add("->换乘"+r.getLine());
path.add(r.getEndStation().getstationName());
}
else
path.add(r.getEndStation().getstationName());
return path;
}`
七.测试用例
搜索线路

查询两站点之间的推荐线路


八.总结
对于java不熟练使得这次编程较为困难,期间从新学习了文件的读等等,并且一开始对于这个系统并没有什么思路,参考了很多的资料,也学习了很多新知识,比如hashmap等等,期间由于不够细心导致有许多小问题,都是基本语法问题导致的bug浪费了很多时间,不过也因此复习了很多java知识



 浙公网安备 33010602011771号
浙公网安备 33010602011771号