42. 接雨水
目录:
题目
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
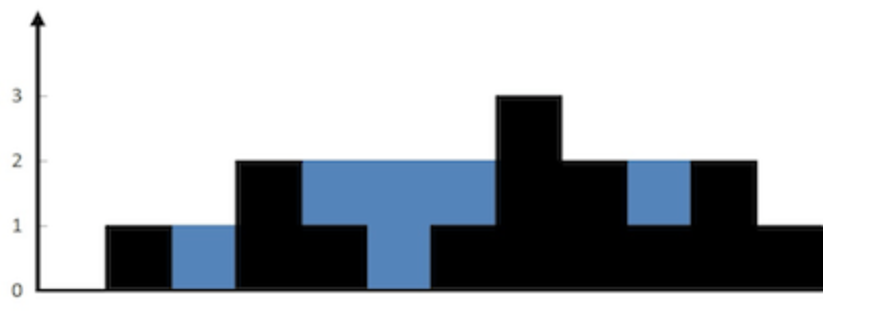
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5] 输出:9
提示:
n == height.length1 <= n <= 2 * 10^40 <= height[i] <= 10^5
第一种方法:动态规划(使用额外的数组存储临时数据)
原理:一个位置处能存储的水的多少与这个位置左、右边的最大值中的最小值有关(木桶原理),如果这个最小值大于当前的高度,则当前位置能存储的雨水为这个高度差。
基于动态规划Dynamic Programming的,算法步骤:
- 我们维护两个个一维的dp数组,这个DP算法需要遍历两遍数组,
- 第一遍遍历,存入i位置左边的最大值到leftMax中,
- 第二遍遍历数组,存入i位置右边的最大值到rightMax中,
- 然后找出左右两边最大值中的较小值,然后跟当前值height[i]相比,如果大于当前值,则将差值叠加到结果
class Solution {
public int trap(int[] height) {
int n = height.length;
if(n < 3)
{
return 0;
}
int[] leftMax = new int[n];
int[] rightMax = new int[n];
for(int i = 1;i<n;i++)
{
leftMax[i] = Math.max(leftMax[i-1],height[i-1]);
}
for(int i = n-2;i>=0;i--)
{
rightMax[i] = Math.max(rightMax[i+1],height[i+1]);
}
int ret = 0;
for(int i = 1;i<n-1;i++)
{
int cur = Math.min(leftMax[i],rightMax[i])-height[i];
if(cur>0)
{
ret += cur;
}
}
return ret;
}
}
第二种方法:改进的动态规划(使用变量存储临时中间数据)
基于上面每一个位置能否存储雨水的原理,我们不必额外的开辟数组存储两边的最大值信息,我们可以先找出数组中的最大值,这样一个位置一侧的最大值就确定(固定)住了,另一侧的最大值,根据上面动态规划中的递推公式,只需要一个变量进行记录更新就行了
class Solution {
public int trap(int[] height) {
int n = height.length;
if(n < 3)
{
return 0;
}
int theMax = height[0];
int maxIndex = 0;
for(int i = 1;i<n;i++){
if(height[i]>height[maxIndex]){
theMax = height[i];
maxIndex = i;
}
}
int ret = 0;
int leftMax = 0;
for(int i = 1;i<maxIndex;i++){
leftMax = Math.max(leftMax,height[i-1]);
int temp = Math.min(leftMax,theMax)-height[i];
if(temp>0){
ret+=temp;
}
}
int rightMax = 0;
for(int i = n-2;i>maxIndex;i--){
rightMax = Math.max(rightMax,height[i+1]);
int temp = Math.min(rightMax,theMax)-height[i];
if(temp>0){
ret+=temp;
}
}
return ret;
}
}
第三种方法:双指针排除移动扫描法
对于位置index,
- 如果能确定这个位置处的储水情况,就可以将指针越过这个位置
- 不能储水,直接跳过
- 能储水,计算此位置处的储水量后,移动跳过
- 对于可能存在的潜在的能储水的左右两个位置,现在还不能肯定的下结论,就只能保持不动
总之,我们是使用两个指针从两边向中间扫,
- 一定不会发生遗漏的需要判断的位置
- 能肯定的下结论的,移动这个指针
- 目前情况下,不能下结论的,指针保持不动
- 彼此间相互判断
实现1
class Solution {
public int trap(int[] height) {
int n = height.length;
if(n < 3)
{
return 0;
}
int ret = 0;
int leftMax = 0,rightMax = 0;
int i = 0,j = n-1;
while(i<=j)
{
//此时i位置处不可能能储水,故i位置处可以排除,移动跳过
while(i<=j && height[i]>=leftMax)
{
leftMax = height[i];
i++;
}
if(i>j)
return ret;
//此时j位置处不可能能储水,故j位置处可以排除,移动跳过
while(j>=i && height[j]>=rightMax)
{
rightMax = height[j];
j--;
}
if(j<i)
return ret;
//此时i,j处如果能储水单侧所需要满足的条件都已经具备,即:
//leftMax>height[i],height[j]<rightMax
else
{
//height[i] < leftMax < rightMax
//此时能够确定i处左右两侧的最大值中的最小者
if(leftMax<rightMax)
{
ret+=leftMax-height[i];
i++;
}
else
{
//leftMax >= rightMax > height[j]
//此时能够确定j处左右两侧最大值中的最小者
ret+=rightMax-height[j];
j--;
}
}
}
return ret;
}
}
实现2
class Solution {
public int trap(int[] height) {
int n = height.length;
if(n<3)return 0;
int ret = 0;
//上一次的leftMax,rightMax初始化值
int leftMax = 0,rightMax = 0;
//本轮即将判断的位置对
int i = 0,j = n-1;
while(i<=j)
{
//先更新一下本轮需判断的位置对i,j的leftMax,rightMax值
//之所以在这个位置更新,是为了防止index超越数组下标范围
//leftMax含义:数组[0,i]范围内的最大值
//rightMax含义:数组[j,n-1]范围内的最大值
leftMax = Math.max(leftMax,height[i]);
rightMax = Math.max(rightMax,height[j]);
if(leftMax<=rightMax)
{
//如果此时i处的值大于它左边的最大值,则i处不能储水
//而根据leftMax值的更新公式,此时的leftMax等于height[i]
//于是i处的储水值等于自己减自己,等于0,虽然i处不能储水,但是
//将它的储水值设定为0增加到ret上,不影响最后的结果
ret+=leftMax-height[i];
i++;
}
else
{
ret+=rightMax-height[j];
j--;
}
}
return ret;
}
}
第四种方法:单调栈
- 栈中保存的元素非递增,作为潜在的卡槽的左挡板,由于栈中元素非递增,相当于卡槽能储水左边需满足的条件自然满足
- 从左到右遍历数组,如果当前元素大于栈顶元素,则当前元素能够作为卡槽的右挡板
- 这个算法是一层一层地计算存储的雨水量的
- 用例子模拟整个过程就可以写出完整的代码(不要技巧化,根据例子直接模拟写代码)
- 栈里保存的是下标,这样我们不丢失由于栈中元素的弹出而导致损失的位置信息
class Solution {
public int trap(int[] height) {
int n = height.length;
if(n <3)
return 0;
int ret = 0;
Deque<Integer> s = new LinkedList<>();
int i = 0;
while(i < n)
{
if(s.isEmpty() || height[i] <= height[s.peek()])
{
s.push(i);
i++;
}
else
{
int index = s.peek(); //作为卡槽的底部
s.pop();
if(s.isEmpty()) //卡槽能储水,至少需要三个元素,左挡板,底部,右挡板
{
s.push(i);
i++;
}
else
ret += (Math.min(height[i], height[s.peek()]) - height[index])*(i-s.peek()-1);
}
}
return ret;
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号