网络流：

主要算法：

  • FF 很垃圾的算法，随机找增广路。
  • EK 比较强的算法，每次找最短增广路以达到多项式复杂度 \(O(nm^2)\)。
  • Dinic 很强的算法，使用BFS分层，多路增广等优化，以达到更优复杂度 \(O(n^2m)\)（在二分图上最多增广 \(\sqrt{n}\) 次，故复杂度为 \(O(\sqrt{n}\times m)\)） 。

费用流：将Dinic的BFS过程改为SPFA。

例题：
（以下题目建图可以参考PPT，题解简易，供复习使用）。

  • POJ1274(down)
    二分图匹配板子。
  • POJ3498(down)
    拆点简单题。
  • POJ1149(down)
    虚点优化建图。
  • SGU326(down)
    题意简述：\(n\) 支球队，球队间进行比赛，已知每支球队目前胜利场数，任意两支球队间还有多少场没有比，问 \(1\) 号球队能否成为冠军（并列也可）
    数据范围：\(1\leq n\leq 20,1\leq others\leq 1000\)。
    先算出一号点最多赢多少次，除 \(S,T\) 外建两排点，第一排是比赛，第二排是队伍，判断是否满流。
  • POJ3281(down)
    太妙啦！
    正常人的思维是建三层点：牛，食物，饮料。但是你发现这个充要条件不好保证。
    于是把牛放中间！！
  • POJ2699
    第一种思路是状压枚举哪些人是strong king，但是复杂度是指数，于是直接倾定得分最大的 \(k\) 个人是strong king，十分合理。
  • SGU438
    增量建图。
    PS：复杂度并不对！约和EK复杂度一样。?
  • SPOJ962
    题目简述：给定无向图 \(G\)，问图上从 \(A\) 到 \(B\)，再从 \(B\) 到 \(C\) 是否存在不经过重复点的路径，数据范围 \(1e5\)。
    与不带权传纸条相似。也与牛-食物-饮料那个相似。
  • [HDU5639]
    题目大意：给一张无向图，一次操作可以选出一些边，要求这些边构成的每个连通块最多一个环，问最小操作次数，数据范围2000。
    一次操作可以改写为：给未分配的一些边分配一些点，要求每个点的出度不能超过 \(1\)，原问题就转化为了在上述操作下，每个点分配边的最大值最小是多少。
    于是二分，然后跑网络流。
  • [HDU1956]
    题意简述：给一张有向边和无向边构成的混合图，问给无向图中的边定向是否可以存在一条欧拉回路，数据范围 \(n\leq 100\)。
    非常妙！
    首先给无向边随意定向，然后计算每个点的入度和出度，定义 \(X_i\) 为该点出度-入度。
    然后建立源点与汇点，然后若 \(X<0\)，则源点向该点连权值为 \(-X/2\) 的边。
    若 \(X>0\)，则该点向汇点连权值为 \(X/2\) 的边。
    然后将无向边反向，权值为 \(1\)。
    这样就可以跑网络流了，满流则有解。
  • POJ2396
    学了一半，留坑。
    有上下界的最大流。
  • Luogu4298
    问题其实是最长反链，在DAG中，最长反链=最小链覆盖。
    最长反链：找一些点，使这些点两两不可达，且数量最多。
    最小链覆盖：选择数量最小的链，覆盖所有点。
    证明：
  1. 最长反链 \(\leq\) 最小链覆盖。考虑若两个点若不通，则他们一定不在一条链上。
  2. 最小链覆盖 \(\leq\) 最长反链。考虑归纳，比较麻烦。

然后可以考虑求最小路径覆盖（求最小路径覆盖所有点，且覆盖的点不重复）
这个就可以网络流/二分图做了。
输出方案的话，把路径上的点补上就行，因为路径以及覆盖所有点了，所以你可以随便补。至于怎么输出最长反链。。wkl都不会，我好像也没啥必要会（雾）

  • Luogu2765
    转换，考虑若干个柱子是若干条链，于是原题等价于最小连覆盖（x+y 是完全平方数就连一条边）。

最小割

最小割=最大流，若能切必须是前缀和后缀冲突！！

  • BZOJ3144
    最小割板子。但是这个切糕模型很重要！！
  • BZOJ1934
    没难点。
  • POJ2987
    难点：
    如何化最大为最小。
    若何化负为正。
  • [HDU1569]
    难点：如何处理前后缀同时冲突，注意观察性质。
  • Luogu4001
    性质：平面图最小割=对偶图最短路。
    非平面图：
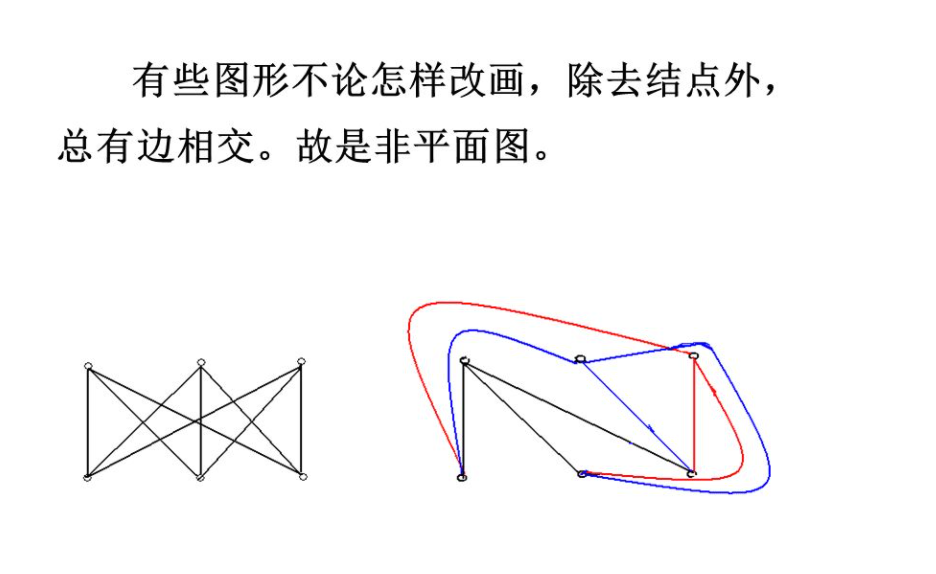
    image

理解图：（每一个割对应对偶图一条路径）
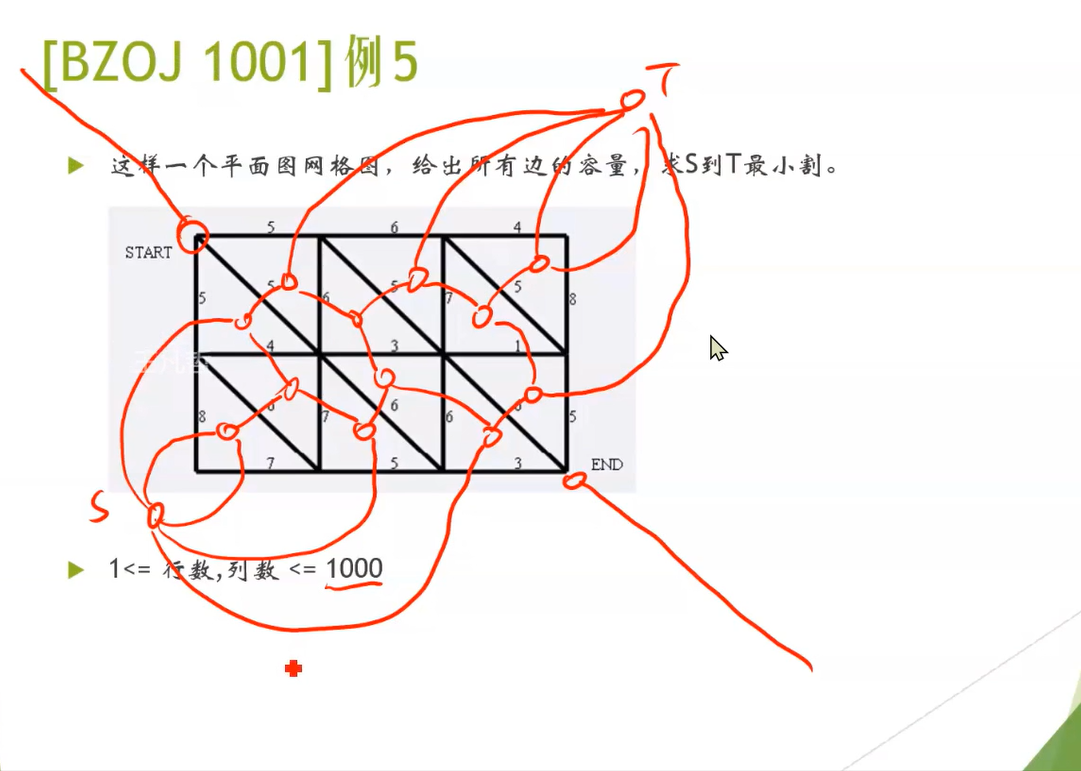
image

妙！当然你也可以试试用最小割跑1e6的Dinic。

费用流

结论是只要每次增广费用最小的，则一定最优。
于是把Dinic改改就行了。

最短路进阶

基础模型

  • BZOJ3417(down)
    和当年加工零件是一道题，维护奇偶最短路。

  • Luogu2865(down)
    严格次短路。和最短路一样做。（能否扩展到k短路？）

  • BZOJ2346(down)
    考虑两点之间的互通关系，跑01最短路。

  • BZOJ2763(down)
    分层图！
    建 \(k\) 层图，层之间免费，然后直接跑最短路。
    当然也可以直接跑二维的最短路，应该比较可以Dij。（？）

  • BZOJ3245(down)
    可以跑二维最短路。
    PPT里的做法是分层图。

  • BZOJ3389(down)
    显然可以贪心，但是我们要用最短路做！！
    考虑首先 \(i+1\) 向 \(i\) 连边权是 \(0\) 的边权，然后 \(l_i\) 向 \(r_i\) 连边权是 \(1\) 的边。

  • BZOJ2118
    喵喵喵。
    先拆，将问题转化为 \([0,i]\) 的问题。
    首先选一个 \(p=a_i\)，然后考虑 \(B \mod p\) 的答案一定位于 \([0,p-1]\)。
    而 \(p\) 又是可以直接凑的，所以说如果你可以算出来 \(B \mod p\) 的最小值是多少。
    然后你就可以每个 \(i\) 向 \(i+a_i\mod p\) 连边权为 \(a_i\) 的边，然后跑最短路就可以算出来 \(B\) 在 \(\mod p\)意义下等于 \(i\) 的最小值，分开考虑，直接算就行。

  • BZOJ1641(down)

  • POJ3613(down)
    只要满足结合律，就可以快速幂！！这样就相当容易优化了。

  • BZOJ4773

    倍增优化。

  • Luogu1119(down)

    先离线，然后将时间排序处理，不断加点，然后直接跑Floyd。

常见构图技巧

  • BZOJ4152(down)
    观察到过山打牛没用，然后就是简单题了。

    分为 \(X\) 轴和 \(Y\) 轴连边。

  • 不知道来自哪的题。
    简述：\(Dis(i,j)=|i-j|\times C\)，然后另有 \(M\) 条有向带权边，求 \(1\sim N\) 的最短路。数据范围 1e5。
    同前面的那个题。

  • CF786B
    线段树优化建图。（如果是前缀连边，可以使用树状数组，然后常数减半）

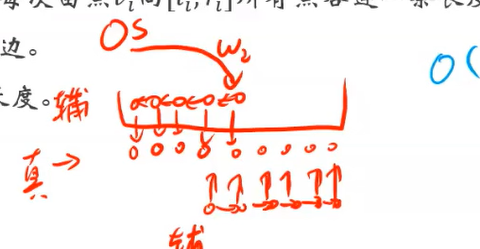
image

  • 分块可以预处理，这样可以 \(O(1)\) 加边。（预处理区间对），感觉码量很大，不太实用。。

最小生成树进阶

主要算法又Kruskal和Prim。

  • POJ2395(down)

    显然 \(A,B\) 间的答案一定在最小生成树的树边上。于是直接输出最小生成树上的最大边即可。

  • BZOJ3714(down)

    发现若询问区间 \([l,r]\)，则相当于是说询问 \(sum_r-sum_{l-1}\)，而若要得到所有 \(i\) 的值，就是要知道所有的 \(sum_i-sum_{i-1}\)，于是现在将问题转化成了求 \(sum_i\)，我们将询问区间 \([l,r]\) 从 \(l-1\) 向 \(r\) 连边，我们发现若对于两个点 \(x,y\)，若他俩直接或间接相连，那么我们一定可以算 \(sum_y-sum_x\)，而我们的目的就是将所有点联系起来，于是直接建图跑最小生成树即可。

  • BZOJ4144(down)

    首先算出每个点到离他最近的加油站的最短距离，那么我们可以将加油站的势力范围划分。

    然后对于一条边 \((u_i,v_i)\)，若他连接的两个点属于不同的加油站，那么对这这两个加油站连边。

    连边后建出最小生成树，每次倍增询问最大值即可。

    正确性证明考虑这张图

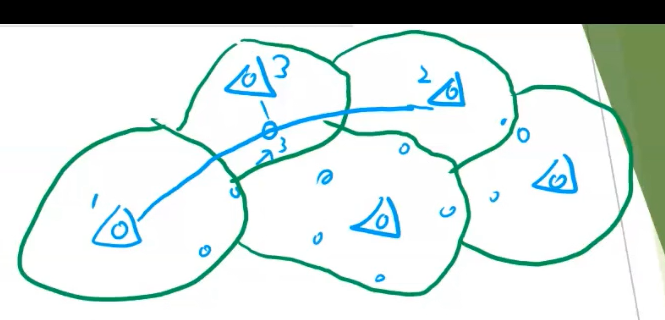
image

证明分为两部分

  • 3号点若可以到2号加油站，则一定到3号加油站
  • 1号加油站\(\sim3\) 的距离一定不小于 \(3\sim\) 3号加油站的距离，那么加完油后剩余油量一定会变大

这也就解释了为何要划分势力。注意码量。。

  • BZOJ2654

    二分一个 \(C\)，然后给白色边附加一个 \(C\) 的权重，显然 \(C\) 值越大，白色边越小。

    但恰好 \(k\) 条白边的时候，此时求出来的最小生成树就是对的。

    那个线性插值不太会啊，有没有哥哥教教啊/kel/kel

拓扑排序

拓扑

简介：应用于 DAG，思路是不断找入度为 \(0\) 的点并删除，大概属于 \(dp\)。

例题：

欧拉路径，回路

  • 有向图欧拉路径充要条件是不存在 \(in_i!=out_i\) 的点或这种点恰有 \(2\) 个。
  • 无向图欧拉路径充要条件是恰存在 \(2\) 个或不存在度数为奇数的点。
  • 不管是要求输出经过点的顺序，还是边的顺序，均需栈实现，正确性未知。
  • 注意使用当前弧优化。

缩点

  • tarjan 寻找强连通的根。
  • 另一个不太常用的算法。
  • 2-SAT

tarjan找割点，需要注意：

  • 注意当该点已经被访问时，可以更新的条件是他在栈中，即他还为构成强连通分量。（图）
    tarjan求割点，需要注意：
  • 对根节点的特判
  • 儿子是已经访问过的点，要用他的dfn值来更新 \(u\) 的low值。

例题：