太难了！/ll

  1. AGC027E ABBreviate
    妙妙题。
    题目有着诸多优良性质！！
    我们将 \(a\) 看作 \(1\)，将 \(b\) 看作 \(2\)，记 \(sum_{l,r}\) 代表 \([l,r]\) 这段区间的区间和。
  • 若 \(sum[l,r]=1\)，则可能有 \([l,r]\) 可以合并为 \(a\)。（只有在 \(ababa\) 时不可合并）。
  • 若 \(sum[l,r]=2\)，则可能有 \([l,r]\) 可以合并为 \(b\)。（只有在 \(babab\) 时不可合并）。
  • 若 \(sum[l,r]=0\)，则这一段一定不可合并！

基于上面的性质，又可以延申出一些性质。

  • 对于一个字符串 \(s\)（可合并），在后面加入新的字符串 \(t\)，若 \(sum_t=0\)，则 \(s+t=s\)。
  • 两个字符串可以联合。

考虑贪心匹配。
不妨假设 \(S\) 一定存在位置 \(i(1\leq i<n)\)，满足 \(S_i\) 与 \(S_{i+1}\) 对应的字符不相同，否则答案一定为 \(1\)。
设原串为 \(S\)，新串为 \(T\)，则 \(T_i\) 一定对应 \(S\) 中一段连续字符，我们假设每个 \(T_i\)，对应都是满足条件的最小前缀，且后缀 \(f\) 满足 \(sum_f=0\),若存在这样的一组匹配，则一定有解。
证明：要证明上述结论，即证明最后一段一定可以被删空，且 \(T\) 不变。

  • 若 \(T_m=f_1\)，那么讲 \(f\) 加到后面即可（因为 \(sum_f=0\)）。
  • 否则，\(T_m\) 对应的 \(s\) 长度一定为 \(1\)，所以将 \(T_m\) 变为 \(f_n\)，递归下去，由于 \(S\) 不交替，所以一定有一组可以。

具体做法：设 \(dp_i\) 代表 \(T_m\) 对应 \(S\) 的第 \(i\) 位方案数，转移简单又显然。

  1. CF1612G Max Sum Array
    首先，对于每个 \(i\)，他的个数为 \(c_i\)，那么考虑它会被加减多少次，显然的是，它会被后面的所有数加，被前面的所有数减，所以我们可以推出第 \(i\) 个贡献为：

\[\sum_{j=1}^{c_i} x_j\times (2\times j-c_i-1) \]

所以，我们成功将原问题转化：
现在有若干系数，以及 \(1\sim n\) 的点，问最大价值，其中，\(n=\sum_{i=1}^m c_i\)。

这个有比较显然的做法，参考这道题，证明不会，留坑。

那么现在瓶颈在于系数，这不好做，我们通过打表和观察发现，每个 \(c_i\) 的系数序列长成这样：

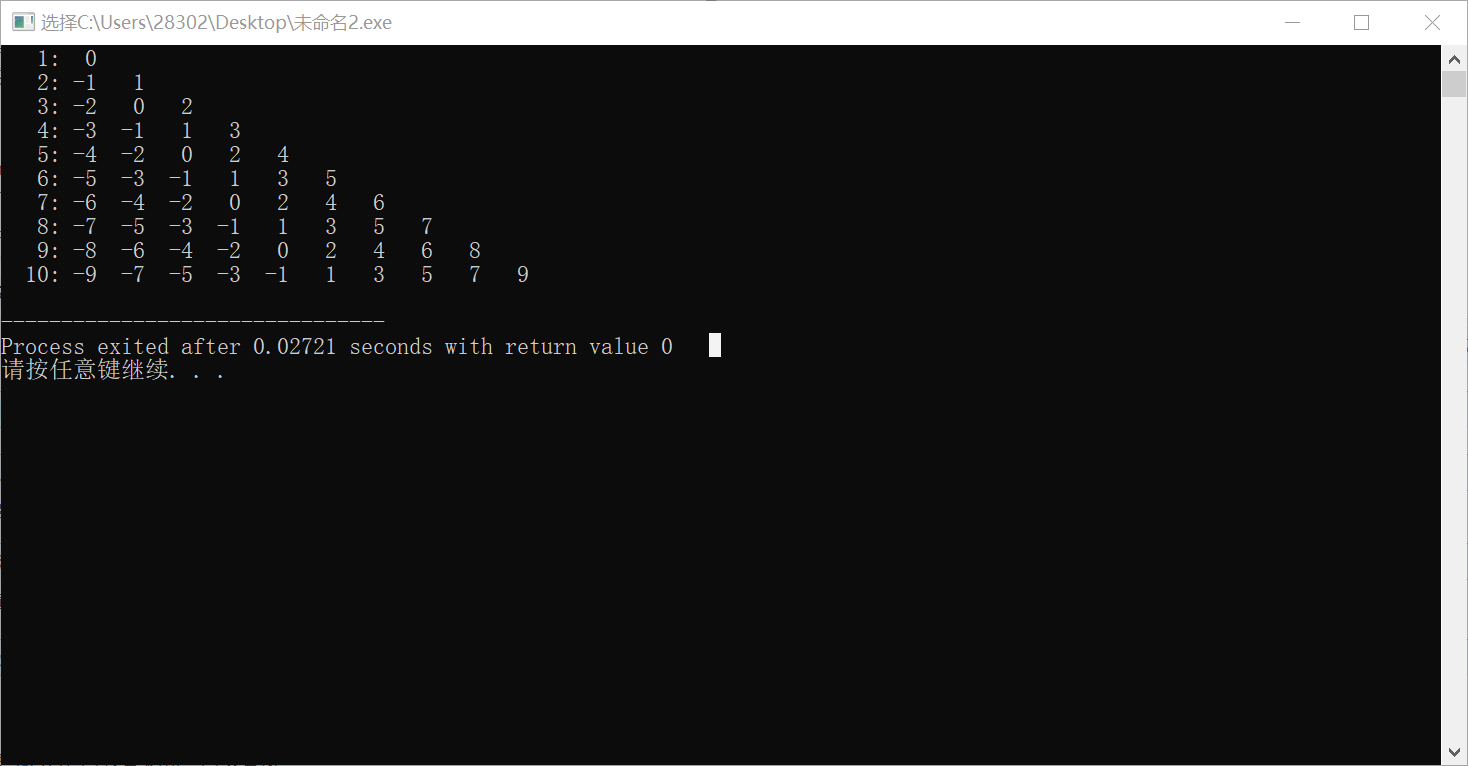
image

这个显然可以维护两颗线段树，分别存奇数和偶数，但是我们发现，该问题本质为区间加，单点查，可以差分！

然后就做完了。

  1. AGC028Chords

首先，圆转序列，性质是，若 \(x,y\) 在圆上有相交，那么他们在线段上也相交！
那么在序列上，设两个联通块为 \(A,B\)，则 \(A,B\) 一定只有两种情况

  • 包含
  • 不相交

那么我们可以考虑每个联通块的贡献，我们设当前计算的联通块为 \([l,r]\)，那么有一段能成为一整个联通块当前仅当

  • \(l\) 与 \(r\) 联通
  • 连通块端点是 \(l,r\)。

设一个连通块内，还有 \(c(l,r)\) 条边是未确定的，\(g(i)\) 是随便填大小为 \(k\) 的连通块的方案数。那么考虑区间dp，设 \(dp[l,r]\) 代表 \(l\sim r\) 这段区间构成一个连通块的方案数（只考虑区间内部），首先，我们将其置于随便选的方案数，但是我们会发现，在这些方案数中，会有一些方案错误，即不连通，所以考虑容斥掉，转移方程为 \(dp[l,r]=g[c[l][r]]-\sum_{k=l}^{r-1}dp[l][k]\times g[c[k+1][r]]\)。
那么，他对整个答案的贡献为：\(dp[l,r]\times g[n-2\times m-c[l,r]]\)。
于是就做完了。

  1. AGC024ESequence Growing Hard
    这个题很妙啊？Minus Orz！
    先摆一些结论，证明自己想：
  • 原问题等价于往里插数
  • 假设在位置 \(q\) 插数，且上一时刻 \(q\) 对应的数字为 \(k\)，插的位置要满足插入的数字 \(p>k\)。
  • 我们假设 \(A_1=x\)，那么将成果按照最左边的 \(x\) 劈开，左子序列满足字典序递增，右子序列满足字典序递增。
  • 右子序列的值域无限制，做子序列的值域为 \([x+1,m]\)。
    那么我们可以考虑设 \(dp_{ij}\) 代表长度为 \(i\) 的子序列，值域在 \([j,m]\) 之间的个数，转移显然。
  1. AGC022FCheckers
    有一个我会证明的性质：
  • 最终系数一定是 \(+(-)2^k\) 的形式。
    还有一些我不会证明的结论，证明以后强大了再证。
  • 若最终形成的系数序列 \(A\) 合法，当且仅当 \(A\) 所有元素和为 \(1\)。
  1. CFGYM103371J Periodic Ruler