数论基础：

素数：

  1. 线性筛素数。
  2. miller_rabin 判素数。
    定理：若 \(n\) 为素数，取 \(a<n\)，设 \(n-1=d\times 2^r\)，则要么 \(a^d\equiv1 \pmod{n}\)，要么存在 \(i(0 \leq i <r)\)，使得 \(a^{d\times2^i}\equiv-1\pmod{n}\)。
    一般选取的质数表：{2,3,5,11,17,19,23,37}。
  3. 质因数分解。
    1.可以暴力筛，时间是根号的。
    2.欧拉筛记录被筛的最小质因数，时间是log的，但是要预处理。
  4. 某定理：对于任意 \(>3\) 的正整数 \(n\) ，都有存在一素数 \(p\)，使得 \(n<p<2\times n-2\)。
    欧拉函数：
    记为 \(\phi(x)\)
    性质：
  5. 该函数为积性函数。
  6. \(\phi(x)= x\prod_{i=1}^n(1-\frac{1}{p_i})\)
  7. 一些有用的证明1 2

逆元：
定义：如果 \((a,m)=1\)且存在唯一的 \(b\) 使得 \(a\times b \equiv1\pmod{m}\) 且 \(1\leq b<m\)，则 \(b\) 为 \(a\) 在模 \(m\) 意义下的逆元。
欧拉定理：\(a^{Ø(m)}\equiv1\pmod{m}\)
线性求逆元：
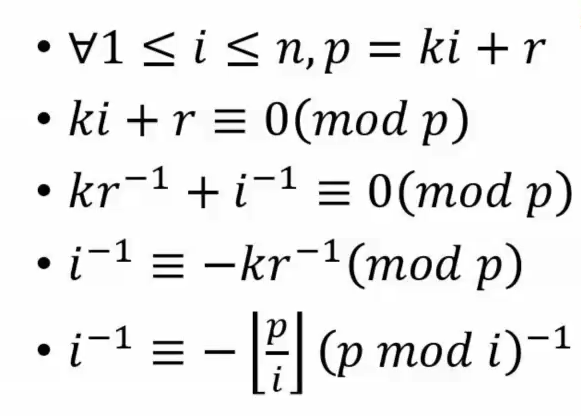
image

扩展欧几里得：
求解方程 \(ax+by=g\)，递归求解。

BSGS：
求解方程 \(a^x\equiv b\pmod{p}\)，思路大概类似于分块，复杂度为根号乘上判存在的复杂度。

中国剩余定理：

  • 大数翻倍法
  • exgcd

组合数：

基本公式：

\(C_n^m=\binom{n}{m}=\frac{n!}{m!(n-m)!}\)

\(P_n^m=\frac{n!}{(n-m)!}\)

多重组合数：

若 \(n=a_1+a_2+a_3+a_4\)，则 \(\binom{n}{a _1,a_2,a_3,a_4}=C_n^{a_1}\cdot C_{n-a_1}^{a_2}\cdot C_{n-a_1-a_2}^{a_3}=\frac{n!} {a_1!a_2!a_3!a_4!}\)。

以下问题均为组合问题，也就意味这若无特殊说明，均不计顺序：

Q1：\(n\) 个不同元素选 \(r\) 个，可重，求方案数。\((C_{n+r-1}^{r})\)

Q2：\(n\) 个不同元素选 \(r\) 个，选择的元素不能相邻，求方案数。\((C_{n-r+1}^{r})\)

Q3：化简 \(\sum_{k=0}^n C(n,k)^2\)。

转化后直接考虑组合意义，答案为 \(C(2n,n)\)。

一些性质：

性质6还不会喂....。

对于不同数据范围组合数取模的几种方式：

  1. \(n\times m\leq 10^7\)。
    直接递推即可。
  2. \(n,m\leq 10^9,p\leq 10^5\)，\(p\) 为质数。
    Lucas板子题（证明）
  3. 在 \(2\) 的条件下，\(p\) 不为质数。
    不会。

概率与期望

试验

这玩意没啥好说的。

样本空间

试验所有结果组成的集合。

事件

样本空间任意一个子集。

事件发生：事件的一个样本点发生。

运算：

  • 包含

  • 相等

  • 互斥（\(∩\)是否是空集）

  • 补（补集）

  • 和（并）

  • 差

  • 积（交）

  • ∪并集符号

  • ∩交集符号

运算律：

  • 交换律
  • 结合律
  • 分配律（？）
  • 对偶律

概率

定义：事件发生的可能性，记为 \(P(A)\)。

若 \(A_1 ∩ A_2......A_n=\varnothing\)，则 \(P(A_1 ∪ A_2...)=P(A_1)+P(A_2)...\)

若 \(B\) 是 \(A\) 的子集，那么 \(P(B-A)=P(B)-P(A)\)。

更一般的，\(P(B-A)=P(B)-P(AB)\)。

还有一些简单的性质就不写了。

条件概率，事件 \(B\) 已经发生的情况下事件 \(A\) 发生的概率为\(P(A|B)=\frac{P(AB)}{P(B)}\)，若独立事件，那么 \(P(AB)=P(A)P(B)\)，\(P(A|B)=P(A)\)。

贝叶斯公式：

\[P(A|B)=\frac{P(B|A)P(A)}{P(B)} \]

若\(B_1,B_2,B_3....B_n\) 是 \(n\) 个样本空间的划分，那么有

\[P(Bi|A)=\frac{P(A|B_i)P(B_i)}{\sum P(A|B_j)P(B_j)} \]

例题（数学题）：

Part1：见zhx课件

Part2：from 数学一本通

  1. \(40\) 支圆珠笔中有 \(30\) 只是黑色的，\(10\) 只是红色的，从中任选 \(4\) 只笔，计算至少有一只是红色的概率，保留 \(1\) 位小数。\((ans=0.7)\)

  2. 一银行卡密码有 \(6\) 位，某人记得他的密码中含有一个 \(1\)，两个 \(2\)，三个 \(3\)，那么问他随机按下密码，正好是正确密码的概率是？

\[ans=\frac{1}{C_6^1+C_5^2+C_3^3} \]

  1. 一个动物活到 \(20\) 岁的概率是 \(0.7\)，活到 \(25\) 岁的概率是 \(0.56\)，已知该动物已经活到了 \(20\) 岁，求他活到25岁的概率。\((ans=\frac{0.56}{0.7})\)

例题（OI题）：

  1. BZOJ 3029守卫者的挑战

期望

杂项

等比数列

假设 \(a\) 为一个等比数列，公比为 \(k\)，那么有：

  • \(a_n=a_1\times k^{n-1}\)。
  • 对于两项\(a_m\)，\(a_n(m\leq n)\)，有\(a_n=a_m\times k^{n-m}\)。
  • 根据上面的性质可以得出\(a_1\times a_n=a_2\times a_{n-1}....=a_i\times a_{n-i+1}=a_1^2\times k^{n-1}\)。
  • 等比数列求和

记 \(S=a_1+a_2+a_3+....+a_n\)。

若 \(k=1\)，则 \(S=a_1\times n\)。

若 \(k>1\)，则

\[S_n=\frac{a_1\times (1-k^n)}{1-k} \]

二项式定理

\((1+x)^n=\sum_{k=0}^nC(n,k)\cdot x^k\)

费马小定理

对于质数 \(p\)，若 \(a\)不是 \(p\)倍数，那么有：

\(a^{p-1}\equiv1\pmod{p}\)

卡特兰数

\(T_0=1,T_n=\sum_{i=0}^{n-1} T_i\times T_{n-i-1}\)

通项公式：\(T_n= \binom{2n}{n} - \binom{2n}{n-1} = \frac{\binom{2n}{n}}{n+1}\)