位运算集合

二进制根据伏羲八卦图的阴阳发展来的。

部分内容摘自《游戏引擎架构》

二进制为什么从右往左读？因为我们的常用电脑是小端架构。

小端：若微处理器储存多字节的最低有效字节于较低的内存位置则该微处理器就是小端处理器。

大端：若微处理器储存多字节的最高有效字节于较低的内存位置则该微处理器就是大端处理器。

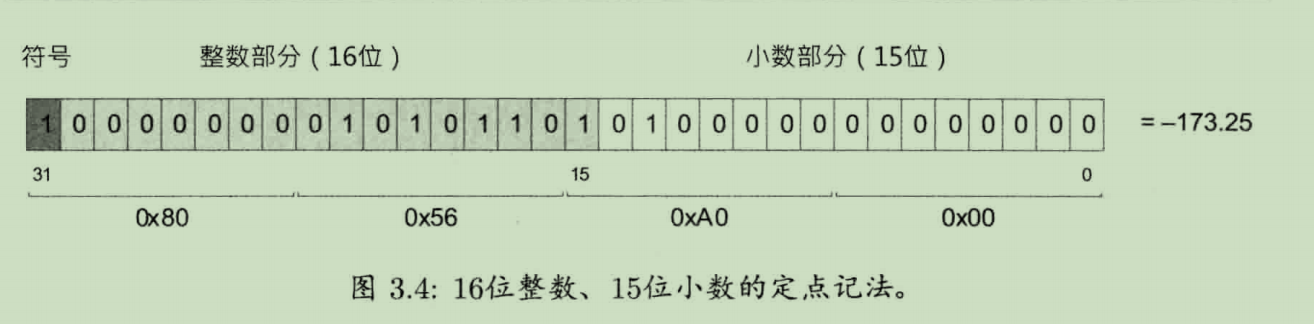
定点记法：

定点记法可随意选择整数部分及小数部分各用多少位去表示。

缺点在于同时限制了可表示的整数部分范围和小数部分精度。

整数部分表示2的递减次幂（二进制转数字部分），小数部分表示2的递减倒次幂（二进制转小数部分）。

 

 

 浮点记法：

小数可以任意移动至不同的位置，此位置由指数控制，一个浮点数由3部分组成：

尾数含有包括小数点前后的相关数字

指数决定那串数字的小数点位于哪里

符号位就是显示该值为正数或负数

可表示的最大值为：0x7f7fffff（3.403*10的38次方）

23位尾数最大值表示为：0x00ffffff

 

 

 

二进制转数字：

例如：00100011

1*2的0次方 + 1*1*2的1次方 + 0*2的2次方+0*2的3次方+0*2的4次方+1*2的5次方

1+2+0+0+0+32=35

二进制数字*2的位数次方

 

数字转二进制：

例如：60
60/2 = 30 余 0
30/2 = 15 余 0
15/2 = 7 余 1
7/2 = 3 余 1
3/2 = 1 余 1

所以十进制数60转为二进制数即为 11100

 

小数转二进制：

例如：0.33

0.33*2=0.66      取0

0.66*2=1.32      取1

0.32*2=0.64      取0 

0.64*2=1.28      取1

0.28*2=0.56      取0

0.56*2=1.12      取1

0.12*2=0.24      取0

0.24*2=0.48      取0

0.48*2=0.96      取0

0.96*2=1.92      取1

..........

所以该小数转二进制是：0.0101010001...

 

二进制转小数：

例如：0.01011

0*1/2 + 1*1/4 + 0*1/8 + 1*1/16 + 1*1/32

0+0.25+0+0.0625+0.03125=0.34375

 

浮点数转二进制：

整数部分+小数部分

例如：60.33

11100.0101010001...

 

二进制计算：

例如：35+47

 0 0 1 0 0 0 1 1
 0 0 1 0 1 1 1 1
 0 1 2 1 2 2 3 2

 把2替换为0，把3替换为1得到：01010010
 2+16+64=82

 

 位运算

TODO:浮点数运算