算法提高课 第一章 动态规划 区间DP

区间DP

282. 石子合并

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;
const int N = 305,INF = 0x3f3f3f3f;
int f[N][N],a[N],s[N];
int n;

int main()
{
    cin>>n;
    for(int i = 1;i <= n;i++)
    {
        cin>>a[i];
        s[i] = s[i-1] + a[i];
    }
    
    for(int len = 2;len <= n;len++) //区间长度为1时，不需要合并，代价为0，故长度从2开始枚举
    {
        for(int i = 1;i + len - 1 <= n;i++)
        {
            int l = i, r = i + len - 1;//左右边界
            f[l][r] = INF;
            for(int k = l;k < r;k++) //分界点 [l,r-1]
            {
                f[l][r] = min(f[l][r],f[l][k] + f[k+1][r] + s[r] - s[l-1]);
            }
        }
    }
    cout<<f[1][n]<<endl;
    return 0;
}

1068. 环形石子合并

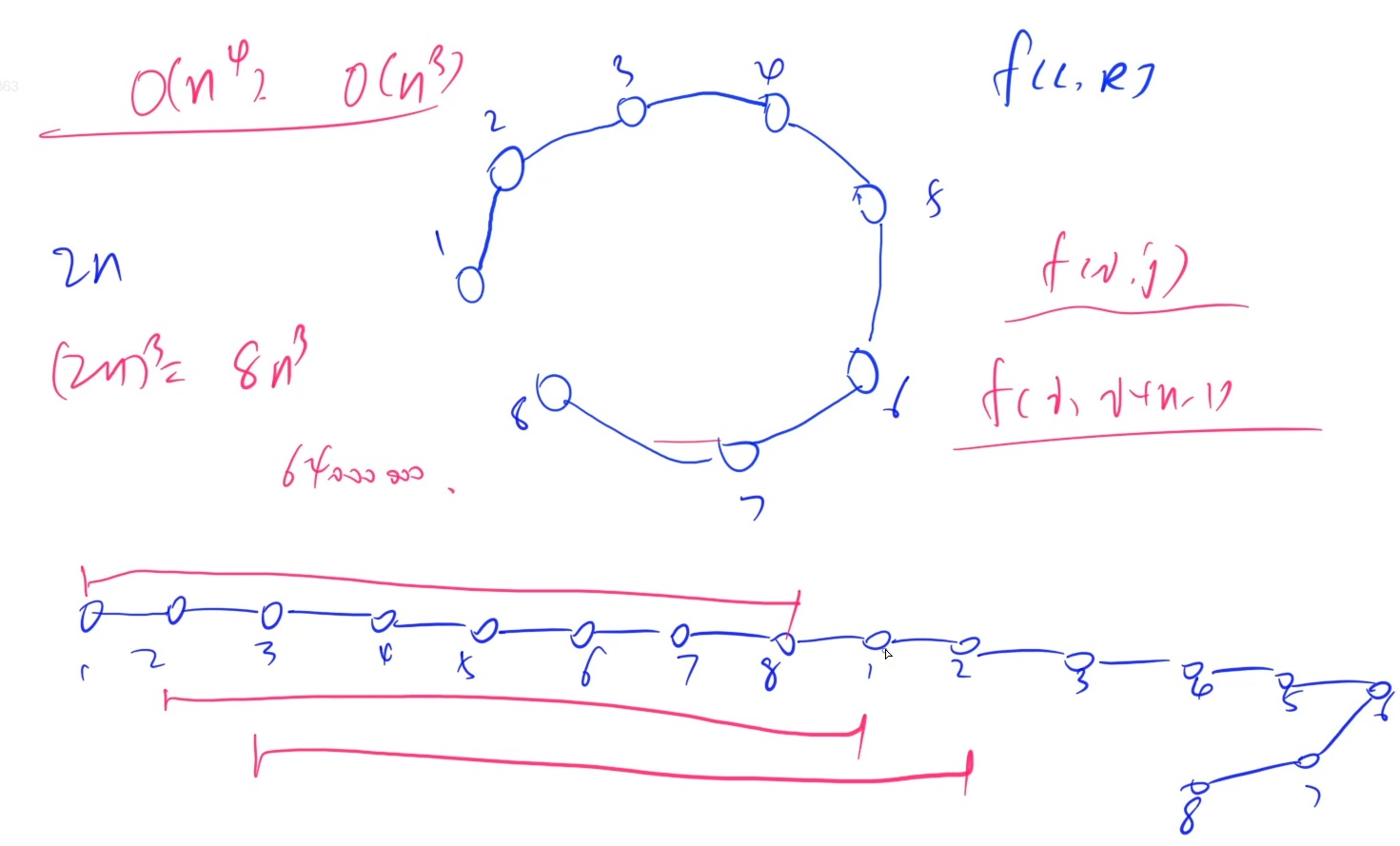
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 410,INF = 0x3f3f3f3f;

int a[N],n;
int f[N][N];//f[l][r]:考虑长度不超过n的区间[l,r]中两两合并的所有方案中，得分总和最大值
int g[N][N];//f[l][r]:考虑长度不超过n的区间[l,r]中两两合并的所有方案中，得分总和最小值
int s[N];//前缀和

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ )
    {
        scanf("%d", &a[i]);
        a[i+n] = a[i];
    }
    for (int i = 1; i <= 2*n; i ++ )
    {
        s[i] = s[i-1] + a[i];
    }
    memset(f,-INF,sizeof f);
    memset(g,INF,sizeof g);
    for(int len = 1;len<=n;len++) //枚举区间长度
    {
        for(int i = 1;i+len-1<=2*n;i++)//枚举区间起点
        {
            int l = i,r = i+len-1;//算出左右端点
            if(len == 1)//注意：若长度为1，无需合并，特殊处理
            {
                f[l][r] = g[l][r] = 0;
                continue;
            }
            for(int k = l;k<r;k++)//枚举中间的合并隔板
            {
                f[l][r] = max(f[l][r],f[l][k] + f[k+1][r] + s[r] - s[l-1]);
                g[l][r] = min(g[l][r],g[l][k] + g[k+1][r] + s[r] - s[l-1]);
            }
        }
    }
    int Max = -1,Min = INF;
    for (int i = 1; i <= n; i ++ ) //由于计算DP的长度为n，破环成链的长度为2n，因此要枚举起点
    {
        Max = max(Max,f[i][i+n-1]);
        Min = min(Min,g[i][i+n-1]);
    }
    cout<<Min<<endl;
    cout<<Max<<endl;
    return 0;
}

320. 能量项链

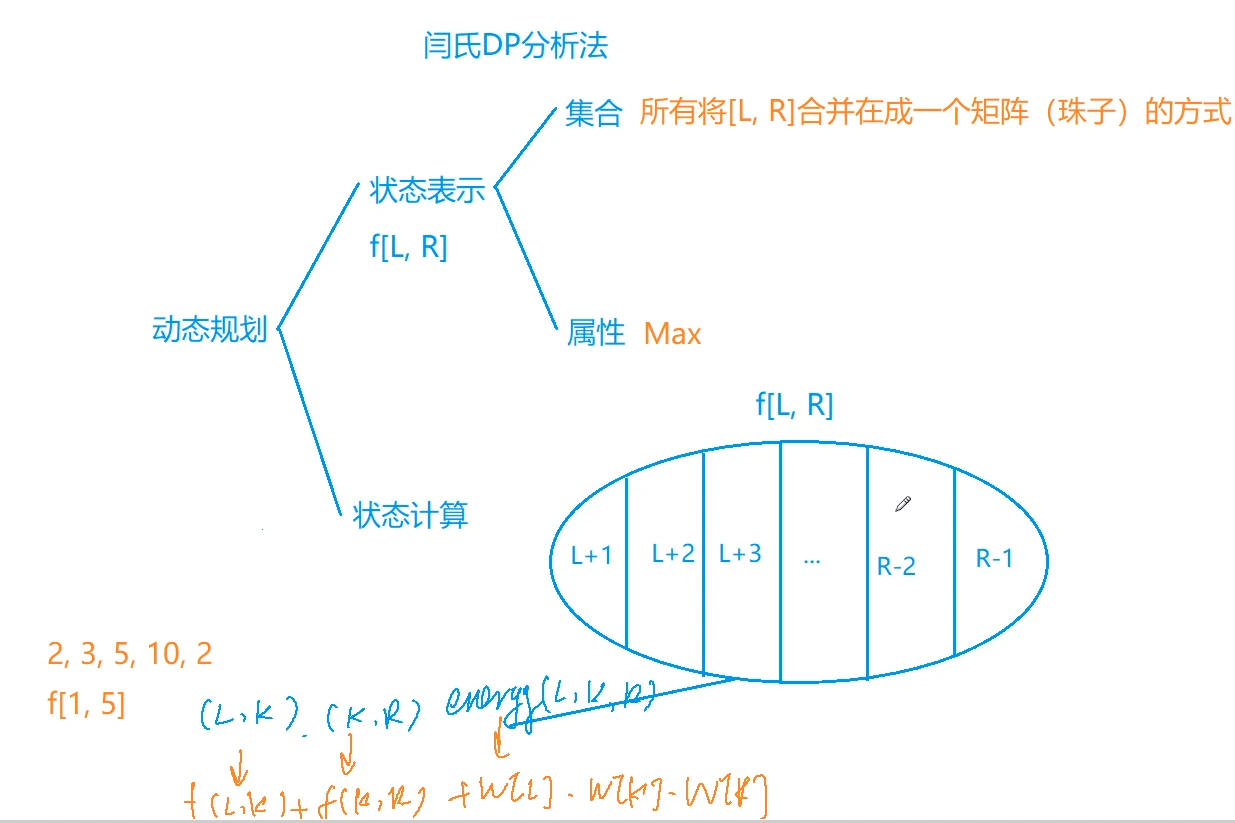
直接当成珠子来看待即可，模拟合并过程。
区间长度为n

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 210;

int a[N],n;
int f[N][N];//f[l][r]:区间[l,r]的所有合并方案中，能量的最大值

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ )
    {
        scanf("%d", &a[i]);
        a[i+n] = a[i];
    }
    memset(f,-0x3f,sizeof f);
    for(int len = 1;len<=n;len++)
    {
        for(int l = 1;l+len-1<=2*n;l++)
        {
            int r = l+len-1;
            if(len == 1)//长度为1，无需合并
            {
                f[l][r] = 0;
                continue;
            }
            for(int k = l;k<r;k++)
            {
                f[l][r] = max(f[l][r],f[l][k] + f[k+1][r] + a[l]*a[k+1]*a[r+1]);//4 5 |5 7 |7 4-> 4 5 7 4
                //这里的过程同石子合并，这里不难想到若将l到k的珠子合并之后会变成一个首是l而尾k+1的珠子；
            //同理若将k+1到r的珠子合并之后会变成一个首是k+1而尾r+1的珠子；
                
            }
        }
    }
    int ans = -1;
    for (int i = 1; i <= n; i ++ )
    {
        ans = max(ans,f[i][i+n-1]);
    }
    cout<<ans<<endl;
    return 0;
}

1069. 凸多边形的划分

区间DP+高精度

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;
typedef long long LL;

const int N = 55;

int a[N],n;
vector<int> f[N][N];

vector<int>add(vector<int>&a,vector<int>&b) //高精度加法
{
    vector<int>c;
    LL t = 0;
    for(int i = 0;i<a.size()||i<b.size();i++)
    {
        if(i<a.size()) t += (LL)a[i];
        if(i<b.size()) t += (LL)b[i];
        c.push_back(t % 10);
        t/=10;
    }
    while(t)
    {
        c.push_back(t % 10);
        t/=10;
    }
    return c;
}
int cmp(vector<int>&a,vector<int>&b) //高精度比大小
{
    if(a.size()!=b.size()) return a.size() > b.size();
    for(int i = a.size()-1;i>=0;i--)
    {
        if(a[i] > b[i]) return 1;
        if(a[i] < b[i]) return -1;
    }
    return 0;
}
vector<int>mul(vector<int>&a,LL b) //高精度乘法
{
    vector<int>c;
    LL t = 0;
    for(int i = 0;i<a.size();i++)
    {
        t += (LL)a[i] * b;
        c.push_back(t % 10);
        t/=10;
    }
    while(t)
    {
        c.push_back(t % 10);
        t/=10;
    }
    return c;
}
void print(vector<int>&a) //输出，注意略去前导0
{
    int i = a.size() - 1;
    while(i>=0 && a[i] == 0) --i;
    while(i>=0) 
    {
        cout<<a[i];
        --i;
    }
    puts("");
}
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ )
    {
        scanf("%d", &a[i]);
    }
    for(int len = 1;len<=n;len++)
    {
        for(int l = 1;l+len-1<=n;l++)
        {
            int r = l + len - 1;
            if(len <= 2)
            {
                f[l][r] = vector<int>{0};
                continue;
            }
            f[l][r] = vector<int>(N,9); //初始化为正无穷
            for(int k = l+1;k<r;k++)
            {
                vector<int>t;
                t.push_back(a[l]);
                t = mul(t,a[k]);
                t = mul(t,a[r]);
                t = add(t,f[l][k]);
                t = add(t,f[k][r]);
                if(cmp(f[l][r],t)>0) f[l][r] = t;
                //f[l][r] = min(f[l][r],f[l][k] + f[k][r] + a[l]*a[k]*a[r]);
            }
        }
    }
    
    print(f[1][n]);
    return 0;  
}

479. 加分二叉树

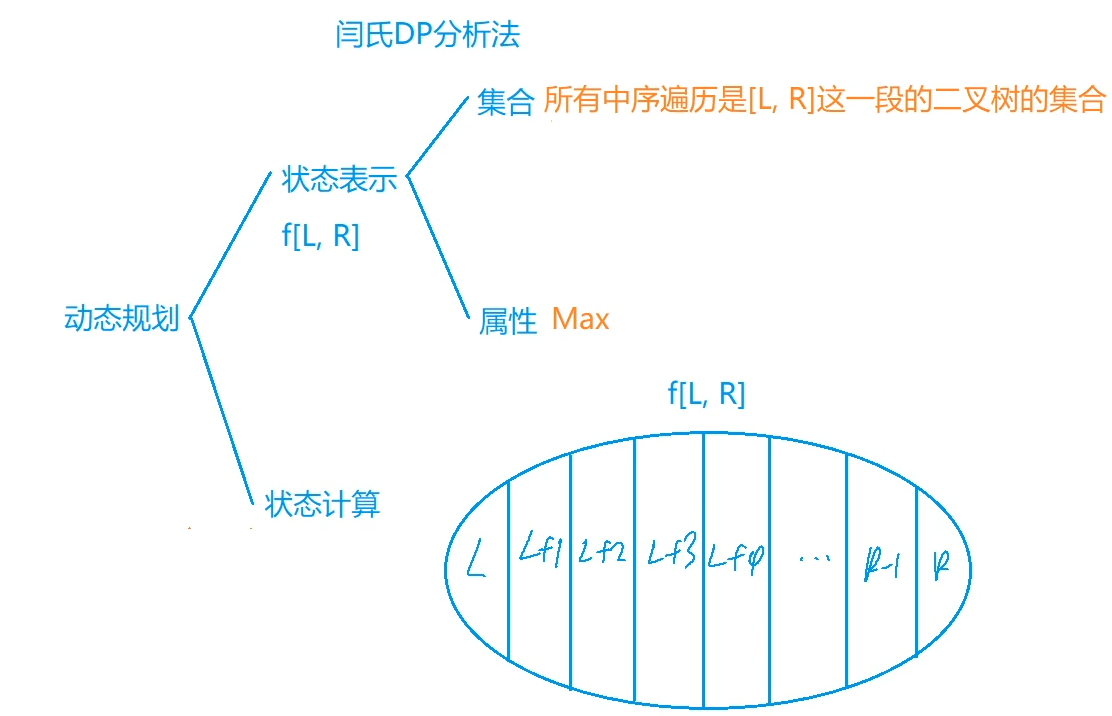
用root[L,R]记录划分方案(根结点)

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 35;

int a[N],n;
int f[N][N];
int root[N][N];

void dfs(int l,int r) //前序遍历
{
    if(l>r) return;
    int t = root[l][r];
    cout<<t<<' ';
    dfs(l,t-1);
    dfs(t+1,r);
    return;
}
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ )
    {
        scanf("%d", &a[i]);
    }
    for(int len = 1;len<=n;len++)
    {
        for(int l = 1;l + len - 1 <= n;l++)
        {
            int r = l+len-1;
            if(len == 1) //若为叶子结点，加分为其本身
            {
                f[l][r] = a[l];
                root[l][r] = l;
                continue;
            }
            for(int k = l;k<=r;k++) //枚举区间每个点当根结点
            {
                int left = k==l?1:f[l][k-1];//若无左子树，左子树为空，加分为1
                int right = k==r?1:f[k+1][r];//若无右子树，右子树为空，加分为1
                int score = left*right + a[k];//subtree的左子树的加分 × subtree的右子树的加分 ＋ subtree的根的分数
                if(score > f[l][r]) //题目要求字典序最小，因此大于再更新
                {
                    f[l][r] = score;
                    root[l][r] = k;
                }
                //f[l][r] = max(f[l][r],f[l][k]*f[k+1][r] + a[k]);
            }
        }
    }
    cout<<f[1][n]<<endl;
    dfs(1,n);
    return 0;
}

321. 棋盘分割

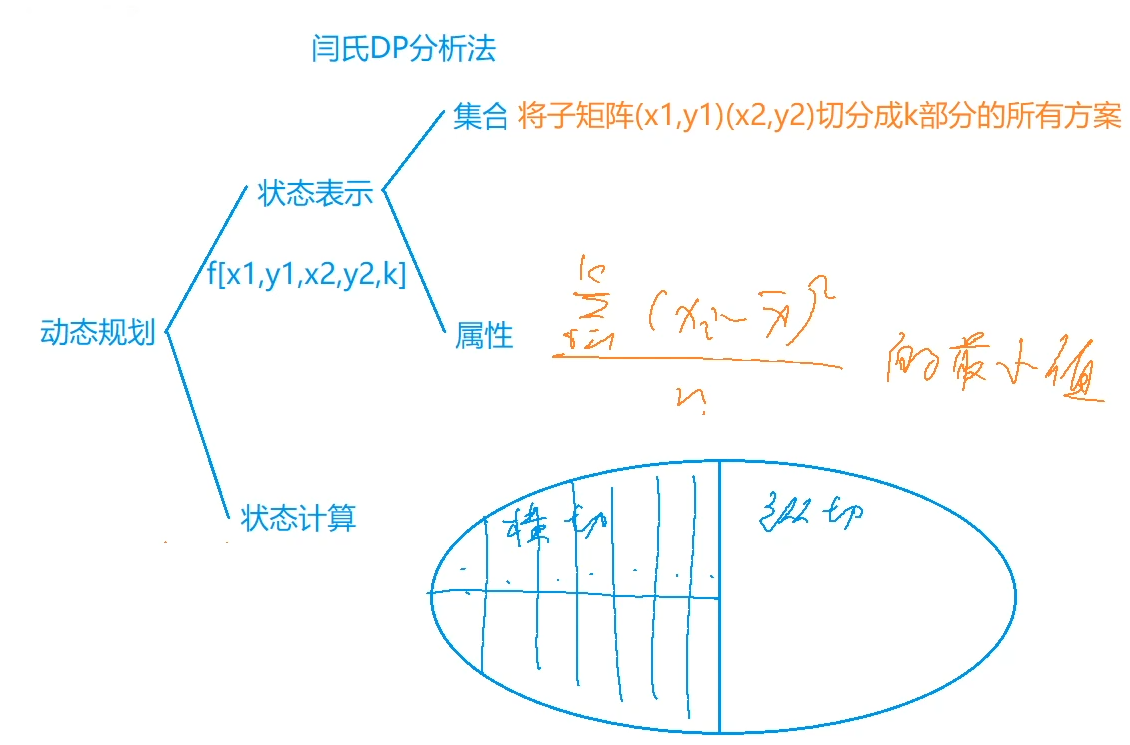
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 10,K = 16,INF = 0x3f3f3f3f;

double f[N][N][N][N][K];//f[x1][y1][x2][y2][k]:(x1,y1)到(x2,y2)区域分成k块的所有方案中，方差和最小的
int s[N][N];//二维前缀和
int n;
double X;

double get(int x1,int y1,int x2,int y2) //计算出(x1,y1)到(x2,y2)区域得分的方差，前缀和O(1)算区域和
{
    double sum = s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1];
    sum -= X;
    return 1.0*sum * sum;
}
double dp(int x1,int y1,int x2,int y2,int k)
{
    double &v = f[x1][y1][x2][y2][k];
    if(v>=0) return v;//记忆化搜索
    if(k == n) return v = get(x1,y1,x2,y2);//注意：分为n块时，仍需要算出矩形区域内的方差
    
    double res = INF;
    for(int t = x1;t<x2;t++)//枚举横着切
    {
        res = min(res,dp(x1,y1,t,y2,k+1) + get(t+1,y1,x2,y2));//切完后取上半部分继续分割，下半部分算方差
        res = min(res,dp(t+1,y1,x2,y2,k+1) + get(x1,y1,t,y2));//切完后取下半部分继续分割，上半部分算方差
    }
    
    for(int t = y1;t<y2;t++)//枚举竖着切
    {
        res = min(res,dp(x1,y1,x2,t,k+1) + get(x1,t+1,x2,y2));//切完后取左半部分继续分割，右半部分算方差
        res = min(res,dp(x1,t+1,x2,y2,k+1) + get(x1,y1,x2,t));//切完后取右半部分继续分割，左半部分算方差
    }
    return f[x1][y1][x2][y2][k] = res;//最后别忘了赋值
}
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= 8; i ++ )
    {
        for (int j = 1; j <= 8; j ++ )
        {
            scanf("%d", &s[i][j]);
            
        }
    }
    for (int i = 1; i <= 8; i ++ )
    {
        for(int j = 1;j<=8;j++)
        {
            s[i][j] += s[i][j-1] + s[i-1][j] - s[i-1][j-1];//计算前缀和
        }
    }
    memset(f,-1,sizeof f);//注意初始化
    X = (double)1.0*s[8][8]/n;//计算总体X的平均值
    
    printf("%.3lf\n",sqrt(dp(1,1,8,8,1)/n));//输出时记得开方
    return 0;
}