一、基于棋盘式(连通性)的状态压缩问题
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
typedef long long LL;//应该是溢出了对吧,所以我们要把所有的f改成long long
const int N=12;//待会儿我会给大家解释一下为什么要开到12
const int M=1<<10,K=110;//K是我们的国王数量
int n,m;//这里用m来表示国王数量,因为我习惯用n来表示一个数然后m来表示另外一个值
vector<int> state; //state 用来表示所有的合法的状态
int id[M];//id的话是存这个每一个状态和这个它的下标之间的映射关系 id有用到吗?好像没有用到
//应该是我之前写的时候思路不太一样,想的时候可能,就是前面设计的思路和实际用到的思路可能会有一点区别
//所以这里其实是不要加id i 的
vector<int> head[M];//这个是每一状态所有可以转移到的其他状态
int cnt[M];/*然后cnt的话存的是每个状态里面 1 的个数,因为我们刚才我们的状态转移方程里面,
其实有一个需要求这个每一个状态里面1的个数的一个过程对吧*/
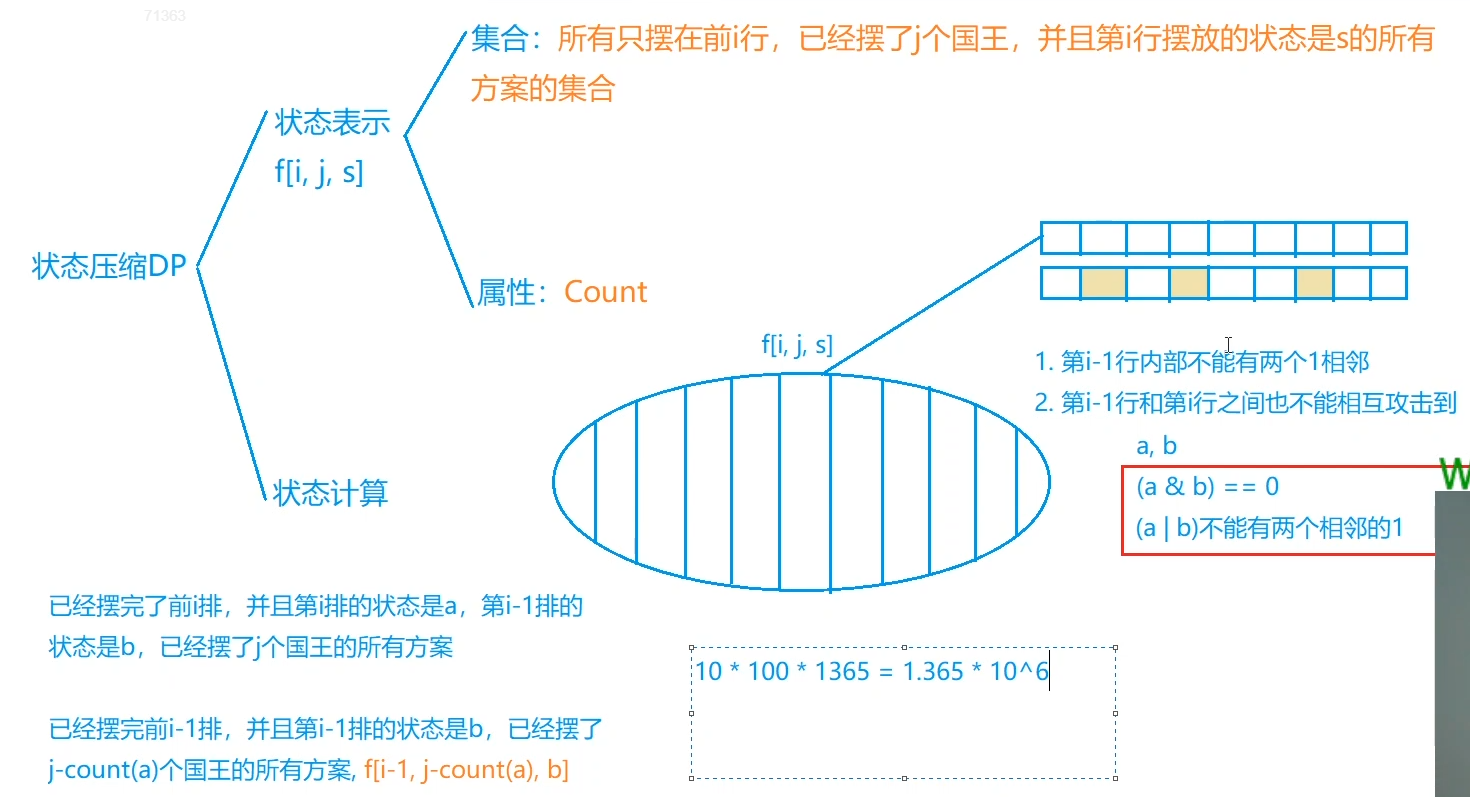
LL f[N][K][M];//这就是我们刚才说的那个状态表示
bool check(int state)
{
for(int i=0;i<n;i++)
if((state >> i & 1)&&(state >> i + 1 & 1))
return false;//如果存在连续两个1的话就不合法
return true;//否则的话就是合法的
}
int count(int state)//这里y总没具体解释,我补充一下,这里就是计算某个数二进制里面1的个数
{
int res=0;
for(int i=0;i<n;i++)res+=state>>i&1;
return res;
}
int main()
{
cin>>n>>m;
//首先我们需要把所有合法状态处理出来对吧,把它预处理一下
for(int i=0;i<1<<n;i++)
if(check(i))
/*check函数是检查一下我们当前状态是不是合法,也就是检查一下我们这个状态里面是不是存在连续的两个1,
如果不存在的话就表示它是合法的*/
{
state.push_back(i);
id[i]=state.size()-1;//id存的是我们这个合法状态对应的下标是多少
cnt[i]=count(i);//cnt的话存的是这个i里面 1 的个数是多少
}
//然后我们来看一下这个不同状态之间的一个这个边的关系
for(int i = 0;i< state.size();i ++ )
for(int j=0;j<state.size();j++)
{
//用a来表示第一个状态,用b来表示第二个状态
int a=state[i],b=state[j];
//这里是建立一个不同状态之间的转移关系
//先预处理一下哪些状态和哪些状态之间可以转移
//首先转移的话是要满足两个条件对吧
//一个是这个 a 和 b 的交集必须要是空集,它必须是空集才可以,否则的话同一列的两个国王会攻击到
//并且的话它们的这个这个并集的话也是需要去满足我们不能包含两个相邻的1的
if((a&b)==0&&check(a|b))
// head[a].push_back(b);
//然后只要这个 b 是合法的,那么我们就把 b 添加到 a 可以转移到的状态集合里面去
//这里y总第一次写错了,debug了
head[i].push_back(j);
//这里是debug过程
//这里写错了,这里应该是head[i].push_back(j);
//因为咱么这里去做的时候用的是下标,不是一个状态的值
}
//好,那剩下的就是 DP 了对吧
f[0][0][0]=1;
//最开始的时候,我们f[0][0][0]=1
/*什么意思呢,就是说,前0行对吧,我们前0行已经摆完了,其实也就是一行也没有摆的情况下,
那么此时由于我们这个是在棋盘外面,
所以肯定每个国王都不能摆对吧,所以我们就只有0这个状态时合法的,那么这个状态的方案数是1*/
//好,然后从前往后枚举每一种状态
for(int i=1;i<=n+1;i++)
for(int j=0;j<=m;j++)//j的话是从0到m对吧,m表示的是国王数量
for(int a=0;a<state.size();a++)//然后我们来枚举一下所有的状态,a表示第i行的状态
for(int b : head[a])//然后来枚举所有a能到的状态
{
//这里要判断一下
//首先要判断的是
//求一下我们a里面的一个1的个数对吧
int c=cnt[state[a]];
//好,然后如果说,呃,就我们的j必须要大于等于c对吧,j是必须要大于等于c的
//为什么呢,因为我们这个表示我们当前这行摆放的国王数量一定要小于等于我们整个的上限对吧
if(j>=c)//如果数说满足要求的话,那么我们就可以转移了
{
f[i][j][a]+=f[i-1][j-c][b];
//转移的话就是f[i][j][a]+=f[i-1][j-c][b],然后从b转移过来
}
}
//好,那我们最终的答案是什么呢?
//我们的最终的答案应该是这个f[n][m][ ],然后最后一维可以直接去枚举对不对
//去枚举一下最后一维是从,就是所有合法状态都是可以的,就最后一行它所有合法状态都是可以的对不对
//那这里的话我们可以偷个懒,不是偷个懒,我们可以有个小技巧,就是我们在枚举i的时候,枚举到n+1就可以了
//就是我们去算到第i+1行,假设我们的棋盘是一个n+1 * n的一个棋盘,多了一行
/*那么我们最终算的时候 就需要输出一个 f[n+1],就是第n+1行,
一共摆到了第n+1行,然后m,然后0,因为第n+1行一个都没摆,对吧*/
cout<<f[n+1][m][0]<<endl;
/*就是我们假设存在第n+1行,但是第n+1行完全没有摆,
那这种情况里面的所有方案其实就是等于这个这个我们只有n行的一个所有方案,对吧*/
/*那这样枚举n+1的一个好处是我们最后不需要再循环枚举最后一行的状态了,
就是我们这个f[n+1][m][0]已经在这个循环里面被循环算出来了*/
//所以可以少一层循环
/*这里的话就是为什么我们一开始N要从12开始,对吧,首先我们要用到11这个下标对吧,
那其实11这个下标是需要开长度是12才可以*/
return 0;
}
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 15,M = 1<<12,mod = 1e8;
int m,n;
int g[N];
vector<int>v; //存放所有一行内的合法方案
vector<int>head[M];//存放所有合法方案的合法转移
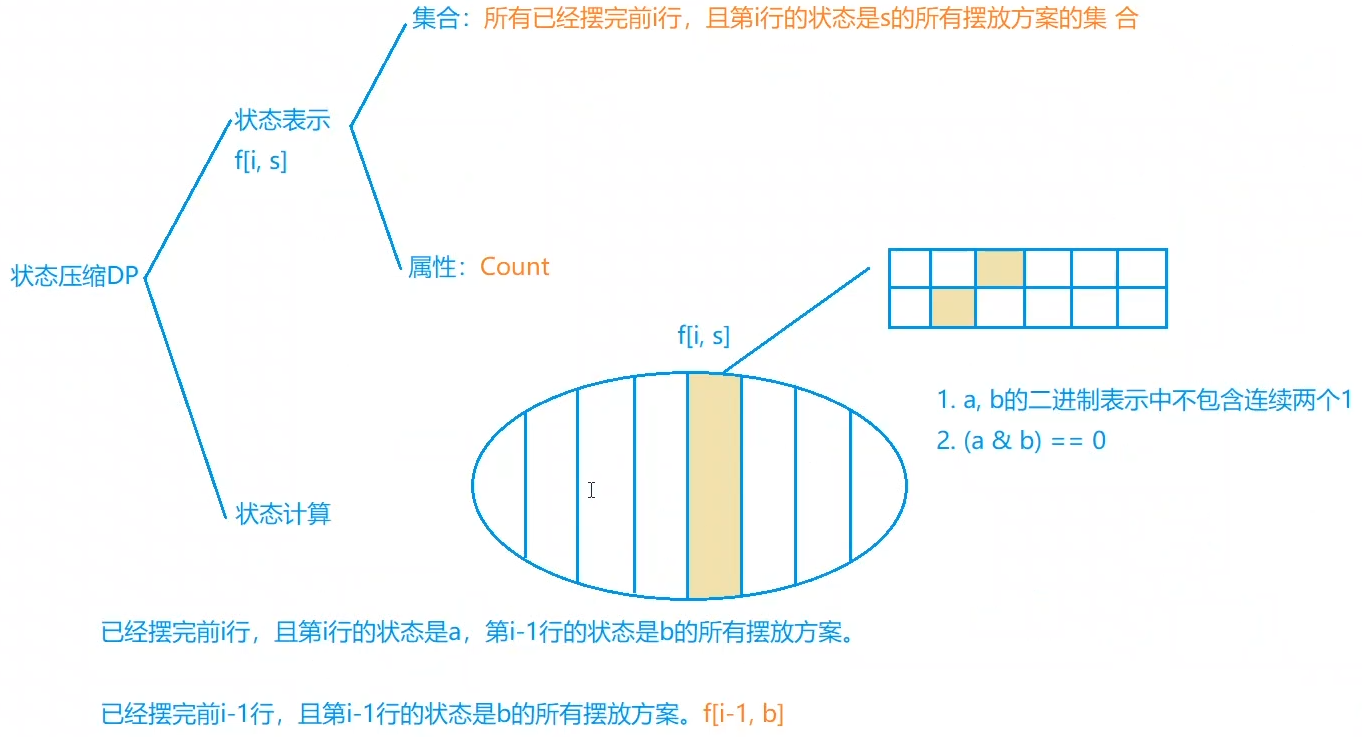
LL f[N][M];//f[i][j]:前i行土地中,最后一行状态为j的所有方案个数
bool check(int state)//检查一行内状态的合法性
{
for (int i = 0; i < n; i ++ )
{
if(state>>i & 1 && state>>(i+1) & 1) return false;//相邻不能种
}
return true;
}
int main()
{
scanf("%d%d", &m, &n);
for (int i = 1; i <= m; i ++ )
{
int t;
for (int j = 0; j < n; j ++ )
{
scanf("%d", &t);
g[i] += (t<<j); //欣赏:二进制状态压缩土地状况
}
}
for (int i = 0; i < 1<<n; i ++ ) //枚举所有方案,筛选一行内合法的方案
{
if(check(i))
{
v.push_back(i);
}
}
for(int i = 0;i<v.size();i++)//枚举所有一行内合法方案,选出合法的状态转移
{
for(int j = 0;j<v.size();j++)
{
int a = v[i],b = v[j];
if((a&b) == 0) //上下相邻不能种
{
head[i].push_back(j);
}
}
}
f[0][0] = 1;//一行也不选,一个也不种的方案唯一
for (int i = 1; i <= m+1; i ++ )//枚举行,m+1行方便算答案
{
for(int a = 0;a<v.size();a++)//枚举所有合法状态
{
for(int b:head[a])//枚举该状态的可转移状态
{
if((g[i] & v[a])!=v[a]) continue; //注意:若当前行土地状况不允许该种植状态,不能种
f[i][a] = (f[i][a] + f[i-1][b]) % mod;
}
}
}
cout<<f[m+1][0]<<endl;//前m+1行,最后一行不种植方案数等价于前m行种植的所有方案个数
return 0;
}
解法1:滚动数组
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 110,M = 1<<11;
vector<int>v;
int g[N];
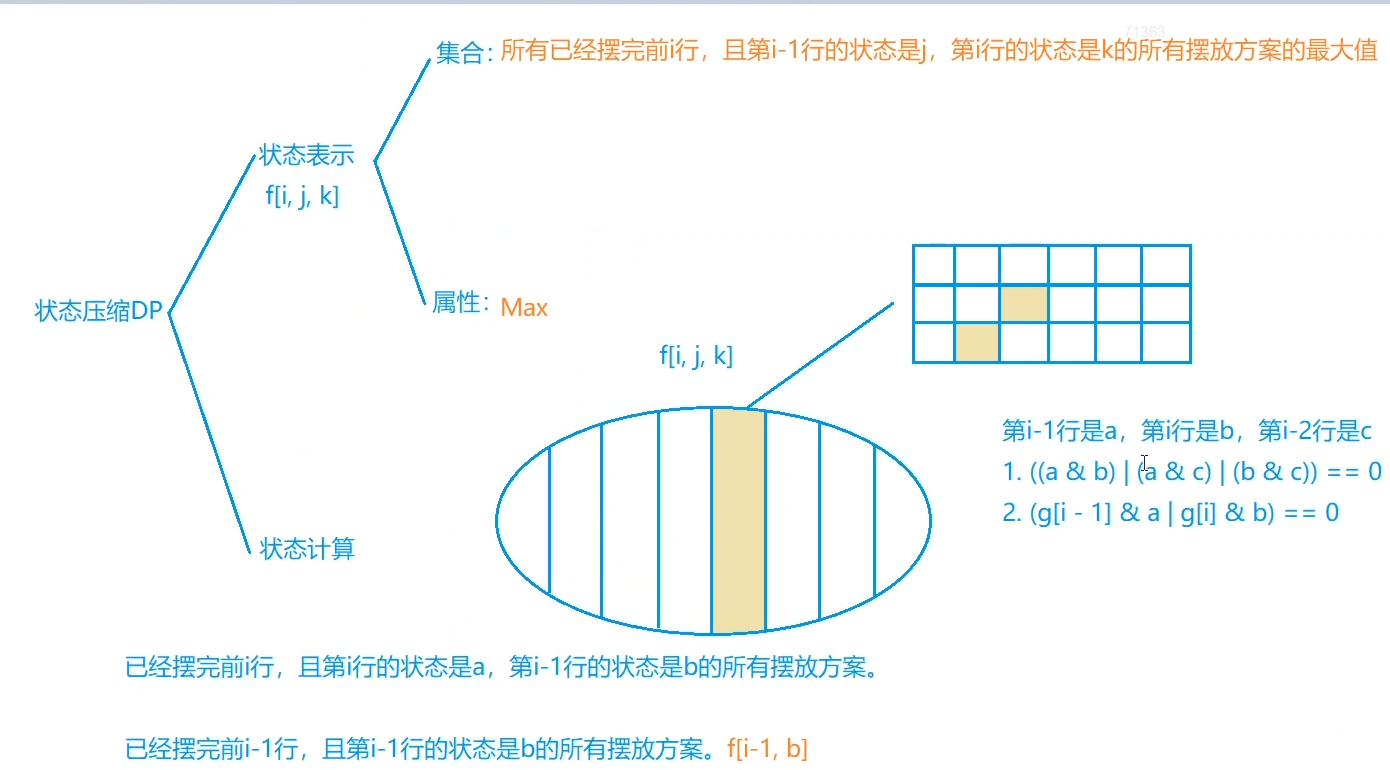
int f[N][M][M];//f[i][j][k]:考虑前i行,最后一行状态为j,倒数第二行状态为k的方案的炮兵个数的最大值
int cnt[M];//二进制中1的数量
int n,m;
int count(int state) //计算1的数量
{
int res = 0;
for(int i = 0;i<m;i++) res += (state>>i & 1);
return res;
}
bool check(int state)//检查一行内状态的合法性
{
for(int i = 0;i<m;i++)//即每行中的1之间距离必须大于2
{
if((state>>i & 1) && ((state>>i+1 & 1)|(state>>i+2 & 1))) return false;
}
return true;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ )
{
char c;
for (int j = 0; j < m; j ++ )
{
cin>>c;
if(c=='H') g[i] += (1<<m-1-j);//将地图以二进制表示读取,1表示高原
}
}
for(int i = 0;i<(1<<m);i++) //处理所有一行内合法的状态
{
if(check(i))
{
v.push_back(i);
cnt[i] = count(i);
}
}
for (int i = 1; i <= n+2; i ++ )//枚举行,到n+2,方便计算最大值
{
for (int j = 0; j < v.size(); j ++ ) //枚举第i行的合法状态
{
for(int k = 0;k<v.size();k++)//枚举第i-1行的合法状态
{
for(int u = 0;u<v.size();u++)//枚举第i-2行的合法状态
{
int a = v[j],b = v[k],c = v[u];
if((a&b)|(b&c)|(a&c)) continue;//三行内不得有同列
if(g[i] & a) continue;//第i行的状态必须符合地图状态
f[i & 1][j][k] = max(f[i & 1][j][k],f[i-1 & 1][k][u] + cnt[a]);
//将i-1行最大值加第i行摆放个数进行比较,选取较大者
}
}
}
}
cout<<f[n+2 & 1][0][0]<<endl;//滚动数组优化:因为每次只同时用到2个状态,减低空间复杂度
return 0;
}
合法转移预处理+滚动数组优化
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 110,M = 1<<11;
int f[2][M][M];
int n,m;
int g[N];
int cnt[M];
vector<int>v;
vector<int>head[M];
bool check(int state)
{
for(int i = 0;i<m;i++)
{
if((state>>i & 1) && ( (state>>i+1 & 1) || (state>>i+2 & 1) ) ) return false;
}
return true;
}
int count(int state)
{
int res = 0;
for(int i = 0;i<m;i++)
{
res += (state>>i & 1);
}
return res;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ )
{
char c;
for (int j = 0; j < m; j ++ )
{
cin>>c;
if(c=='H') g[i] += (1<<j);
}
}
for (int i = 0; i < 1<<m; i ++ )
{
if(check(i))
{
v.push_back(i);
cnt[i] = count(i);
}
}
for (int i = 0; i < v.size(); i ++ ) //枚举两行间的合法转移
{
for(int j = 0;j<v.size();j++)//
{
int a = v[i],b = v[j];
if(!(a&b)) head[a].push_back(b);
}
}
for (int i = 1; i <= n + 2; i ++ ) //枚举第i行
{
for(int j = 0;j<v.size();j++) //枚举合法状态
{
if(v[j] & g[i]) continue;
for(int k:head[v[j]])//枚举该状态可合法到达的所有状态,作为i-1行
{
for(int u:head[k])//枚举该状态可合法到达的所有状态,作为i-2行
{
if(u & v[j]) continue;//不能放高原处
f[i & 1][v[j]][k] = max(f[i & 1][v[j]][k],f[i-1 & 1][k][u] + cnt[v[j]]);
}
}
}
}
cout<<f[n+2 & 1][0][0]<<endl;//滚动数组优化空间+n+2技巧
return 0;
}
二、基于集合的状态压缩DP
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
#define x first
#define y second
using namespace std;
typedef pair<double, double> PDD;
const int N = 18, M = 1 << 18;
const double eps = 1e-8;
int n, m;
PDD q[N];
int path[N][N];
int f[M];
int cmp(double x, double y)
{
if (fabs(x - y) < eps) return 0;
if (x < y) return -1;
return 1;
}
int main()
{
int T;
cin >> T;
while (T -- )
{
cin >> n >> m;
for (int i = 0; i < n; i ++ ) cin >> q[i].x >> q[i].y;
memset(path, 0, sizeof path);
for (int i = 0; i < n; i ++ )
{
path[i][i] = 1 << i;
for (int j = 0; j < n; j ++ )
{
double x1 = q[i].x, y1 = q[i].y;
double x2 = q[j].x, y2 = q[j].y;
if (!cmp(x1, x2)) continue;
double a = (y1 / x1 - y2 / x2) / (x1 - x2);
double b = y1 / x1 - a * x1;
if (cmp(a, 0) >= 0) continue;
int state = 0;
for (int k = 0; k < n; k ++ )
{
double x = q[k].x, y = q[k].y;
if (!cmp(a * x * x + b * x, y)) state += 1 << k;
}
path[i][j] = state;
}
}
memset(f, 0x3f, sizeof f);
f[0] = 0;
for (int i = 0; i + 1 < 1 << n; i ++ )
{
int x = 0;
for (int j = 0; j < n; j ++ )
if (!(i >> j & 1))
{
x = j;
break;
}
for (int j = 0; j < n; j ++ )
f[i | path[x][j]] = min(f[i | path[x][j]], f[i] + 1);
}
cout << f[(1 << n) - 1] << endl;
}
return 0;
}





 浙公网安备 33010602011771号
浙公网安备 33010602011771号