MATLAB 第四章 符号计算

课程导入

数值计算：必须先对变量赋值，然后才能参与运算，运算结果是数值。
符号计算：无须事先对变量赋值，而将所得到结果以标准的符号形式来表示。

符号计算特点

1. 运算对象可以是没赋值的符号变量
2. 以推理解析的方式进行运算，因此不受计算误差累积所带来的困扰

一、符号对象和符号表达式

1.符号对象

符号变量、符号常量、符号数字、符号矩阵、符号表达式和符号函数
任何符号对象必须借助专门的sym或syms定义
任何包含符号对象的表达式、方程也一定是符号对象

2.符号常量

当数值常量作为sym()的输入变量时，就建立了符号常量，虽然看上去是一个数值量，但已经是一个符号对象了

3.符号变量(内容可变的符号对象)

符号变量的命名规则和数值变量的命名规则相同

创建符号变量

单个符号变量创建函数sym

多个符号变量创建函数syms

符号矩阵创建

syms a b c d
A=[a,b;c,d]

自由符号变量

确定规则

默认首选x
然后与x的ASCII码值之差的绝对值小的字母优先
字母优先次序为x(120),y(121),w(119),z(122),v(118)等
symvar(expression):按英文字母表的顺序列出式中所有符号变量
symvar(expression,n):按靠近x的ASCII顺序列出n个符号变量

syms u z v w a;
f = sym(3);
eq = sin(f)*u*z^2+v*z+f*w-a;
symvar(eq)
symvar(eq,3)
ww = solve(eq,w)
ww = solve(eq,a)

4.符号表达式

符号表达式是由符号常量、符号变量、符号函数运算符以及专用函数连接起来的符号对象。
符号表达式包括：符号函数和符号方程。
区别：符号函数不带等号，符号方程带等号

5.符号函数

6.符号方程

7.符号计算的运算符

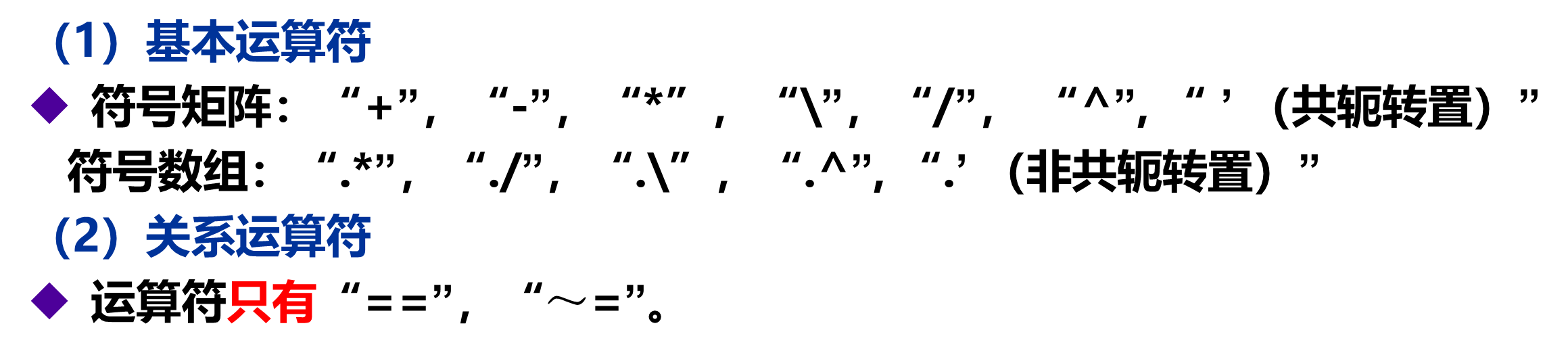
二、符号运算中的函数运算

符号计算与数值计算的区别

1. 数值计算保留8位有效位数，每次数值计算有一定的截断误差；符号计算不进行数值运算，无截断误差。
2. 符号计算时间较长，数值计算时间较短
3. 数值计算必须先对变量赋值；符号计算无需先赋值，但必须先定义，计算结果以标准的符号表达式形式给出。

二、符号数字及表达式操作

符号数字和数值数字很像，但是他们的类型不同，将影响他们的使用。比如：一些数值函数不接受符号数字，而只接受数值数字。

1.数值数字转符号数字

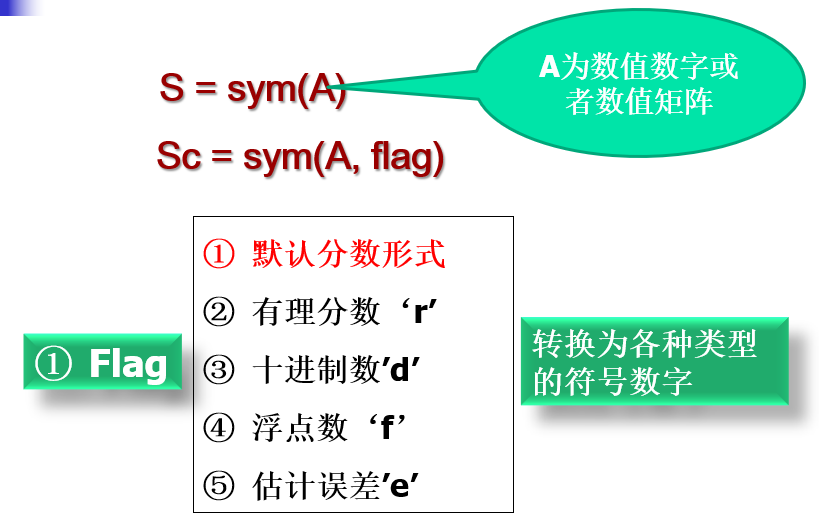
2.符号数字转数值数字

num = double（num）:符号数字转为数值数字
B = eval(A):符号矩阵转为数值矩阵

3.符号数字的任意精度限制

数值计算则会出现舍入误差（双精度浮点型，64位）
符号运算是在完全准确的情况下进行的；但是计算时间长，存储空间大。
需要控制符号运算中参加变量有效数字个数
控制有效位的函数：vpa(x,n)
x是符号或数值，有效位数为n位，默认32

>> format long %显示15位数值有效位
>> 1/2+1/3
ans = 0.833333333333333
>> ss=sym(1/2+1/3)
ss =5/6
>> sv=vpa(1/2+1/3,6)
 sv =0.833333

4.符号表达式的基本操作

simplify化简各类表达式

R = simplify(S)
运用simplify指令将S转换成最简短形式
注：S可以是符号表达式或符号矩阵。

syms x;
f = (1/x^3+6/x^2+12/x+8)^(1/3)
g = simplify(f)

5.符号表达式的置换操作

自动提取

>> syms a b c d W
>> [V,D]=eig([a b;c d]) %求解符号矩阵的特征值D与特征向量V
 V =
[ (a/2 + d/2 - (a^2 - 2*a*d + d^2 + 4*b*c)^(1/2)/2)/c - d/c,
  (a/2 + d/2 + (a^2 - 2*a*d + d^2 + 4*b*c)^(1/2)/2)/c - d/c;1, 1]

>> [RVD,W]=subexpr(V,W)
RVD =
[ (a/2 - W/2 + d/2)/c - d/c, (W/2 + a/2 + d/2)/c - d/c]
[                         1,                                              1]
 
W =
(a^2 - 2*a*d + d^2 + 4*b*c)^(1/2)

人为指定

R = subs(S,Old,New)
新符号变量New替代原来符号表达式S中的变量Old
数值代替所有符号变量则结果转化为数值数据。

syms x y
ss = x - sin(x)-1/sin(x);
ss1 = subs(ss,sin(x),y)
ss2 = subs(ss,x,4)

多重替换：R = subs(S,{old1,old2,...},{New1,New2,...})

三、符号微积分

1.符号表达式F的极限(limit)

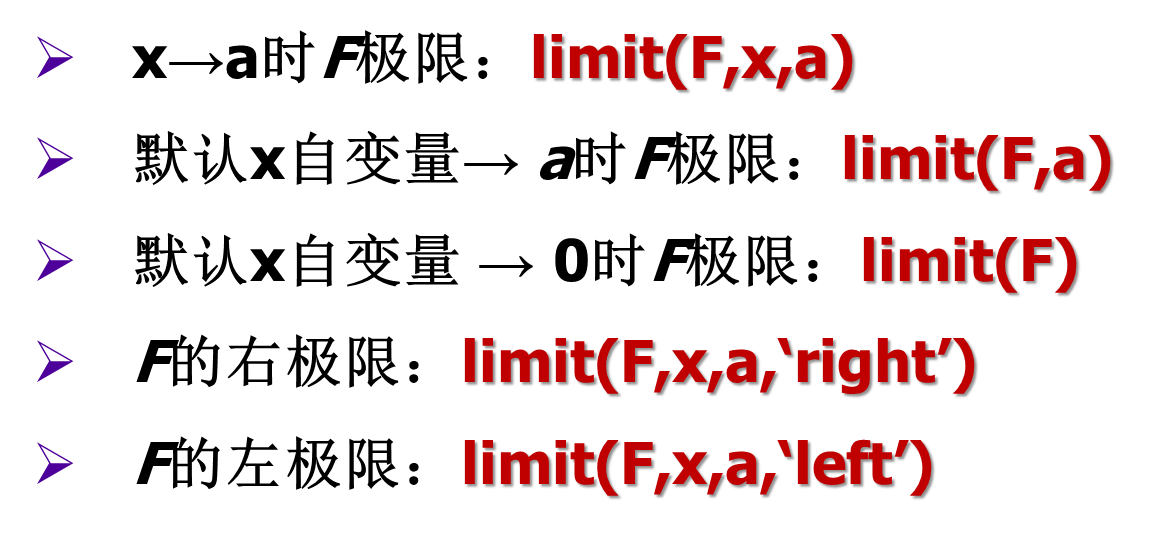
syms x k
y = (1 - 1/x)^(k*x)
limit(y,x,inf)

2.符号表达式F的求导(diff)

syms t x
f = [t^3 - exp(x),t/x;t*cos(x),log(x)];
dfdx = diff(f,x)
d2fdt2 = diff(f,t,2)
dfdtdx = diff(diff(f,t),x)

syms x y
g = (x^3*y - 5*y)/(2*x^2 + 7);
dg = diff(g,y)
res = subs(dg,[x,y],[1,2])

3.符号表达式F的积分(int)

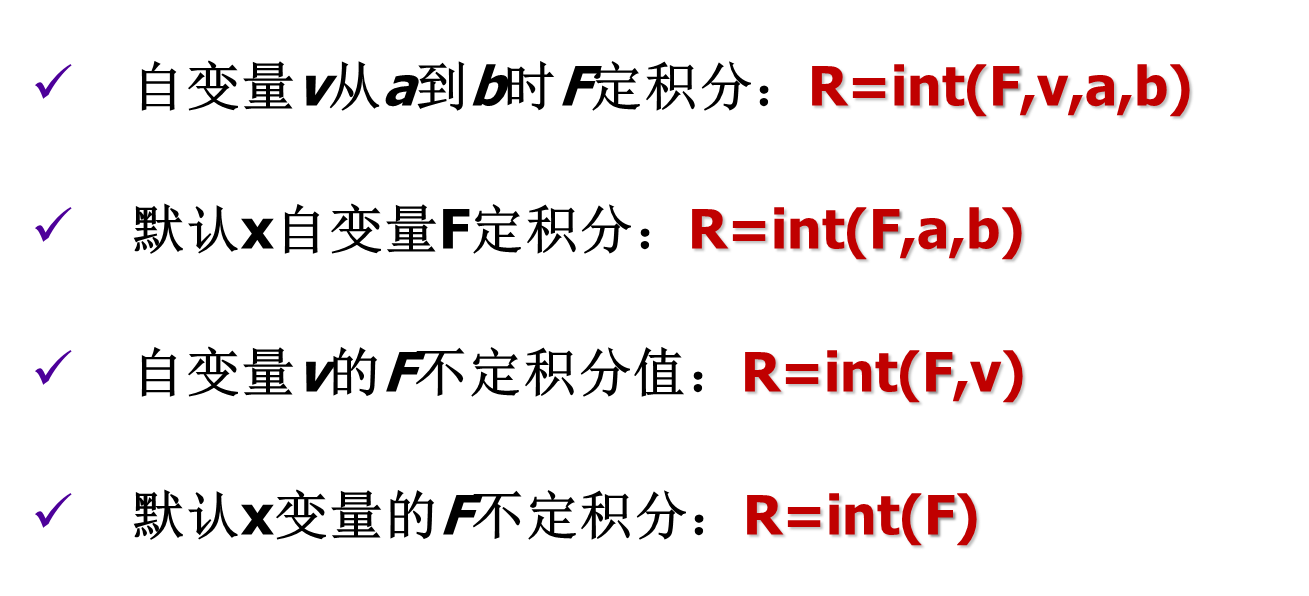
4.级数求和(symsum)

5.泰勒级数(taylor)

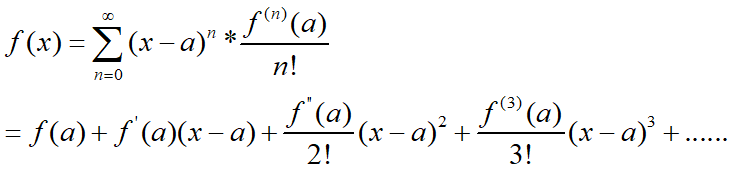
4.符号方程求解