Acwing 第五章 动态规划(一)
Acwing 第五章 动态规划(一)
一、01背包问题
n个物品,容量为v的背包,每个物品有两个属性:体积vi,价值wi,每件物品只能用一次,目标求出最大价值是多少?

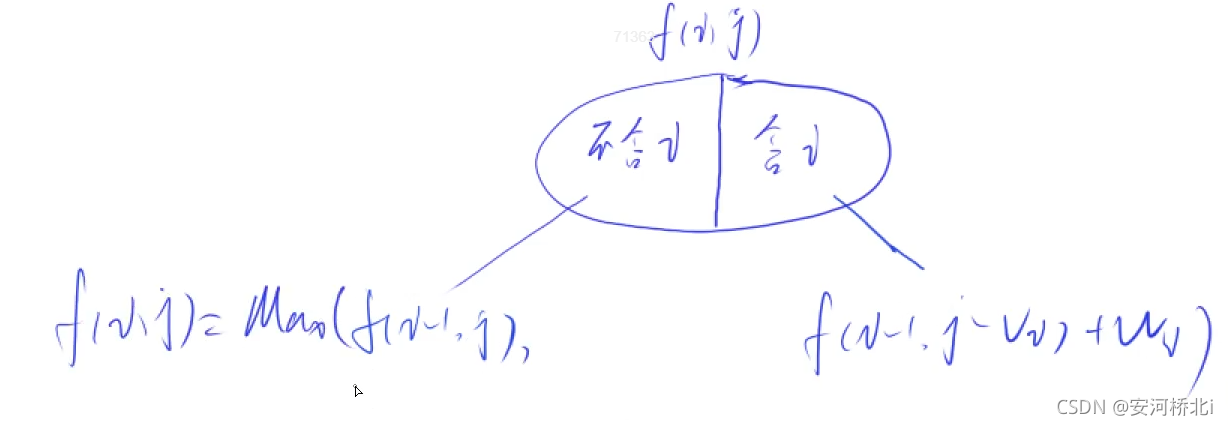
f(i,j) 从1 - i 个物品中选,总体积不超过 j
集合:表示所有的选法
状态计算
#include<iostream>
using namespace std;
const int M = 1005;
int n,m;//物品数量和背包体积
int v[M],w[M];//表示某件物品的体积和价值
int f[M][M];//状态表示:包含所有选法的集合
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>v[i]>>w[i];
//f[0][0~M]全部初始化为0
for(int i=1;i<=n;i++) //枚举前i件物品
{
for(int j=1;j<=m;j++)//枚举不超过j的体积
{
if(v[i] > j) f[i][j] = f[i-1][j];//当前背包容量装不进第i个物品,则价值等于前i-1个物品
else f[i][j] = max(f[i-1][j],f[i-1][j-v[i]]+w[i]);//能装,需进行决策是否选择第i个物品
}
}
cout<<f[n][m]<<endl;
}
二、完全背包问题
n个物品,容量为v的背包,每个物品有两个属性:体积vi,价值wi,每件物品可以用无限次,目标求出最大价值是多少?
朴素做法:超时
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1010;
int v[N],w[N];
int f[N][N];
int n,m;
int main()
{
cin>>n>>m;
for(int i = 1;i <= n;i++) cin>>v[i]>>w[i];
for(int i = 1;i <= n;i++)
{
for(int j = 0;j <= m;j++)
{
for(int k = 0;k * v[i] <= j;k++)
{
f[i][j] = max(f[i][j],f[i-1][j - k*v[i]] + k*w[i]);
}
}
}
cout<<f[n][m]<<endl;
return 0;
}
优化做法
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1010;
int v[N],w[N];
int f[N];
int n,m;
int main()
{
cin>>n>>m;
for(int i = 1;i <= n;i++) cin>>v[i]>>w[i];
for(int i = 1;i <= n;i++)
{
for(int j = v[i];j <= m;j++)//优化版必须从v[i]开始枚举
{
f[j] = max(f[j],f[j - v[i]] + w[i]);
}
}
cout<<f[m]<<endl;
return 0;
}
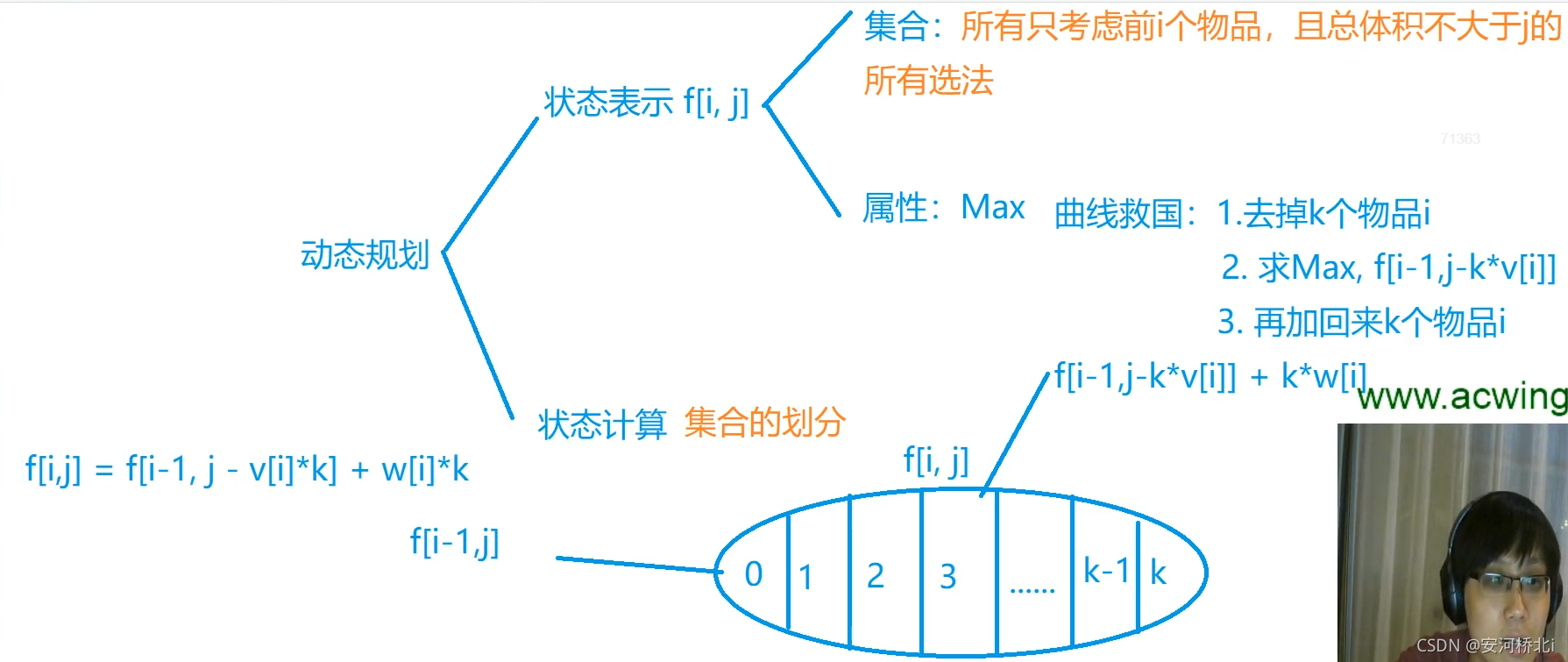
三、多重背包问题
n个物品,容量为v的背包,每个物品有两个属性:体积vi,价值wi,每件物品最多有si个(每件物品的si不一样),目标求出最大价值是多少?
朴素做法(0<N,V≤100,0<vi,wi,si≤100)
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
int v[N],w[N],s[N];
int f[N][N];
int n,m;
int main()
{
cin>>n>>m;
for(int i = 1;i <= n;i++) cin>>v[i]>>w[i]>>s[i];
for(int i = 1;i <= n;i++)
{
for(int j = 0;j <= m;j++)
{
for(int k = 0;k <= s[i] && k * v[i] <= j;k++)
{
f[i][j] = max(f[i][j],f[i-1][j - k * v[i]] + k * w[i]);
}
}
}
cout<<f[n][m]<<endl;
return 0;
}
优化版(0<N≤1000,0<V≤2000,0<vi,wi,si≤2000)
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 25005; //最多会拆分出1000*log2000个物品
int n,m,v[N],w[N];
int a,b,s;//某件物品的体积,价值和个数
int f[N];//表示所有选法的集合
int main()
{
cin>>n>>m;
int cnt = 0;
for(int i = 1;i <= n;i++)
{
cin>>a>>b>>s;
int k = 1;//当前2的某次幂,用于把物品尽量拆分成2的次幂的个数
while(k <= s)
{
cnt++; //维护当前拆分的所有物品的个数
v[cnt] = a * k;//k个物品,每个占据a体积
w[cnt] = b * k;//k个物品,每个物品有b价值
s -= k;//维护当前未拆分的物品个数
k = k << 1;//k向左移位
}
if(s > 0)//剩下的物品个数不能被拆分成更大的2的次幂,故全部分为一组
{
cnt++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt;//更新当前拆分后物品的个数
for(int i = 1;i <= n;i++) //01背包优化版
{
for(int j = m;j >= v[i];j--)//优化后必须从m开始递减枚举
{
f[j] = max(f[j],f[j - v[i]] + w[i]);
}
}
cout<<f[m]<<endl;
return 0;
}
四、分组背包问题
n组物品,每次物品里有若干个,每个组里面最多选一个物品,容量为v的背包,每个物品有两个属性:体积vi,价值wi,每件物品只能用一次,目标求出最大价值是多少?
第一行有两个整数 N,V,用空格隔开,分别表示物品组数和背包容量。
接下来有 N 组数据:
每组数据第一行有一个整数 Si,表示第 i 个物品组的物品数量;
每组数据接下来有 Si 行,每行有两个整数 vij,wij,用空格隔开,分别表示第 i 个物品组的第 j 个物品的体积和价值;
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
int v[N][N],w[N][N];//第i组第j个物品的体积和价值
int s[N];//每一组的物品个数
int f[N];//所有选法集合
int n,m;
int main()
{
cin>>n>>m;
for(int i = 1;i <= n;i++)
{
cin>>s[i];//第i组物品个数
for(int j = 1;j<=s[i];j++)
{
cin>>v[i][j]>>w[i][j];//第i组第j个物品的体积和价值
}
}
for(int i = 1;i <= n;i++)//枚举组的序号
{
for(int j = m;j >= 1;j--)//优化后必须从m开始递减枚举背包体积
{
for(int k = 1;k <= s[i];k++)//枚举某组中第k个物品
{
if(v[i][k] <= j)//若第i组第k件物品的体积小于背包体积
{
f[j] = max(f[j],f[j - v[i][k]] + w[i][k]);//价值较大才选择
}
}
}
}
cout<<f[m]<<endl;
return 0;
}
五、线形DP
898. 数字三角形
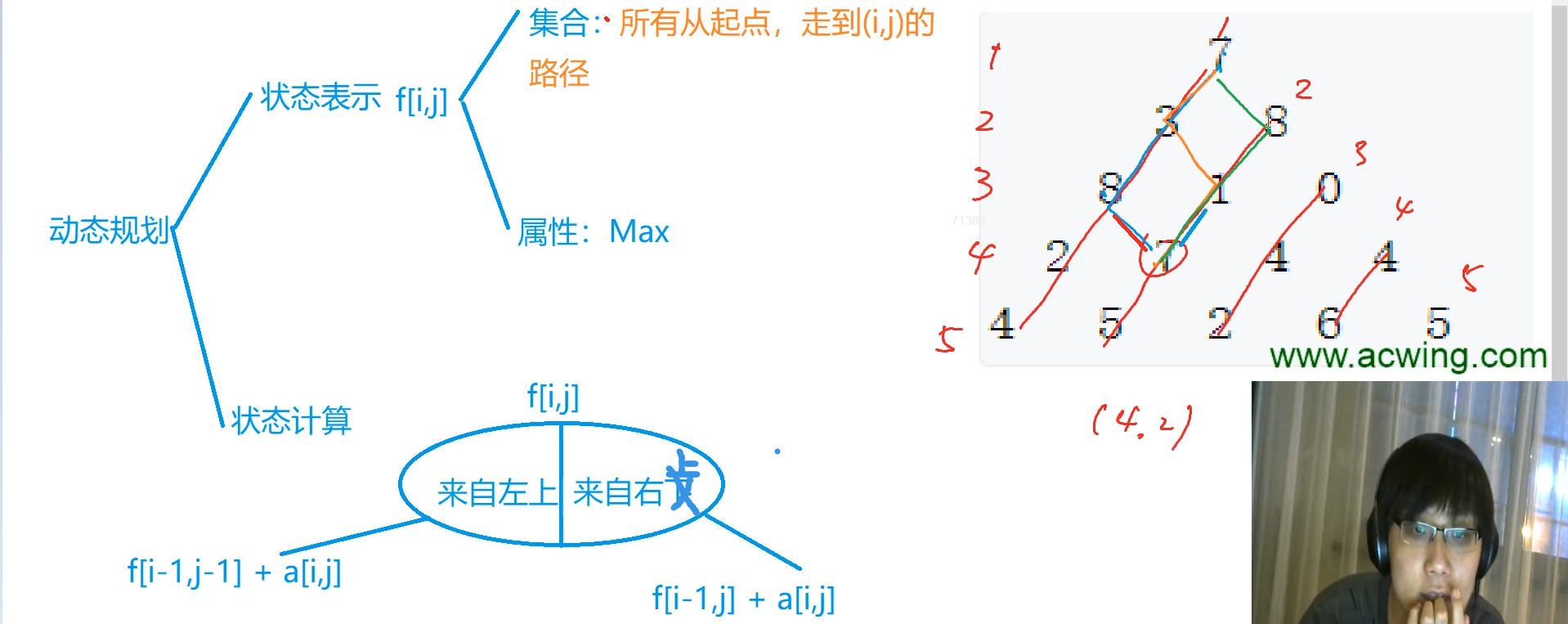
O(N^2)
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 505,INF = 0x3f3f3f3f;
int a[N][N];//数字三角形
int f[N][N]; //状态表示:当前第i行第j列数字和的最大值
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
cin>>a[i][j];
}
}
memset(f,-INF,sizeof f);//必须把方案表示数组全部初始化成负无穷
//因为在状态计算时,计算边界数字时会发生越界,负无穷可以解决此类问题
f[1][1] = a[1][1];//第一个数的和最大值一定是本身
for(int i=1;i<=n;i++) //从第二行开始枚举计算
{
for(int j=1;j<=i;j++)
{
f[i][j] = max(f[i-1][j-1]+a[i][j],f[i-1][j]+a[i][j]);//取左上方路径与右上方路径数字和的最大值加其本身就是答案
}
}
int Max = -0x3f3f3f3f;
for(int i=1;i<=n;i++)
{
Max = max(Max,f[n][i]);//答案取最后一行最大值
}
cout<<Max<<endl;
return 0;
}
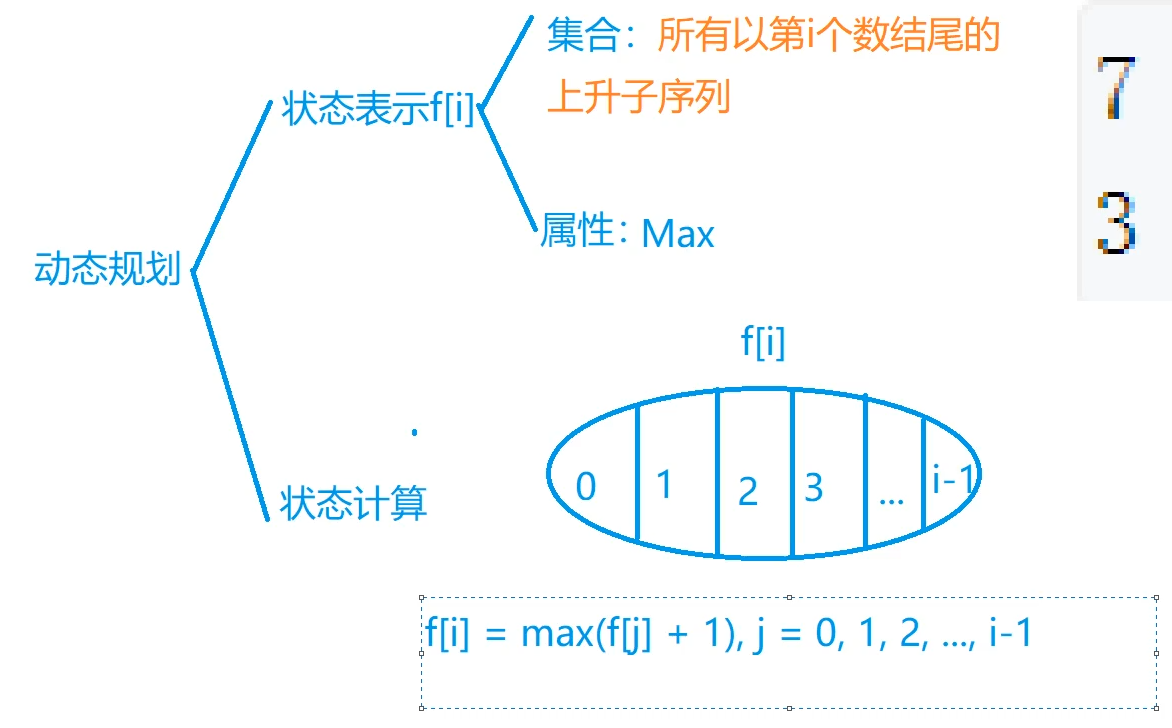
895. 最长上升子序列
O(N^2)
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1005;
int n,a[N];
int f[N];
int main()
{
cin>>n;
for(int i = 1;i <= n;i++)
{
cin>>a[i];
}
for(int i = 1;i <= n;i++)
{
f[i] = 1; //初始化,集合里只有a[i]这一个数
for(int j = 1;j < i;j++) //从1~i-1枚举,若j比i小,则根据个数考虑将f[j]集合与a[i]合并
{
if(a[j] < a[i])
{
f[i] = max(f[i],f[j] + 1);
}
}
}
int res = -1;
for(int i = 1;i<=n;i++) //比较每一个集合,选取个数最多的那个
{
res = max(res,f[i]);
}
cout<<res<<endl;
return 0;
}
求具体方案的集合元素
for(int i = 1;i <= n;i++)
{
f[i] = 1; //初始化,集合里只有a[i]这一个数
g[i] = 0;//表示集合里只有a[i]本身
for(int j = 1;j < i;j++) //从1~i-1枚举,若j比i小,则根据个数考虑将f[j]集合与a[i]合并
{
if(a[j] < a[i])
{
if(f[i] < f[j] + 1)
{
f[i] = f[j] + 1;
g[i] = j;
}
}
}
}
int res = -1,k;
for(int i = 1;i <= n;i++) //比较每一个集合,选取个数最多的那个
{
if(res < f[i])
{
res = f[i];
k = i;
}
}
while(k!=0)
{
printf("%d ",a[k]);
k = g[k];//递推
}
puts("");
cout<<res<<endl;
896. 最长上升子序列 II
给定一个长度为 N 的数列,求数值严格单调递增的子序列的长度最长是多少。
输入格式
第一行包含整数 N。
第二行包含 N 个整数,表示完整序列。
输出格式
输出一个整数,表示最大长度。
数据范围
1≤N≤100000,
−109≤数列中的数≤109
单调栈+二分(O(NlogN))
#include<iostream>
using namespace std;
const int N = 1e5+10;
int a[N],stk[N],top=0;
int n;
int find(int x) //二分查找单调栈中最小的大于等于x的数
{
int l = 1,r = top;
while(l <= r)
{
int mid = l+r>>1;
if(stk[mid] >= x)
{
r = mid - 1;
}
else l = mid + 1;
}
return l;
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i];
}
stk[++top] = a[0]; //第一个数入栈
for(int i = 1;i < n;i++)
{
if(a[i] > stk[top]) stk[++top] = a[i]; //若当前数大于栈顶,入栈
else //否则找到栈中大于等于a[i]的最小的数,用a[i]替换
{
int p = find(a[i]);
stk[p] = a[i];
}
}
// for(int i = 1;i<=top;i++)
// {
// cout<<stk[i]<<" ";
// }
cout<<top<<endl; //输出栈中元素个数
return 0;
}
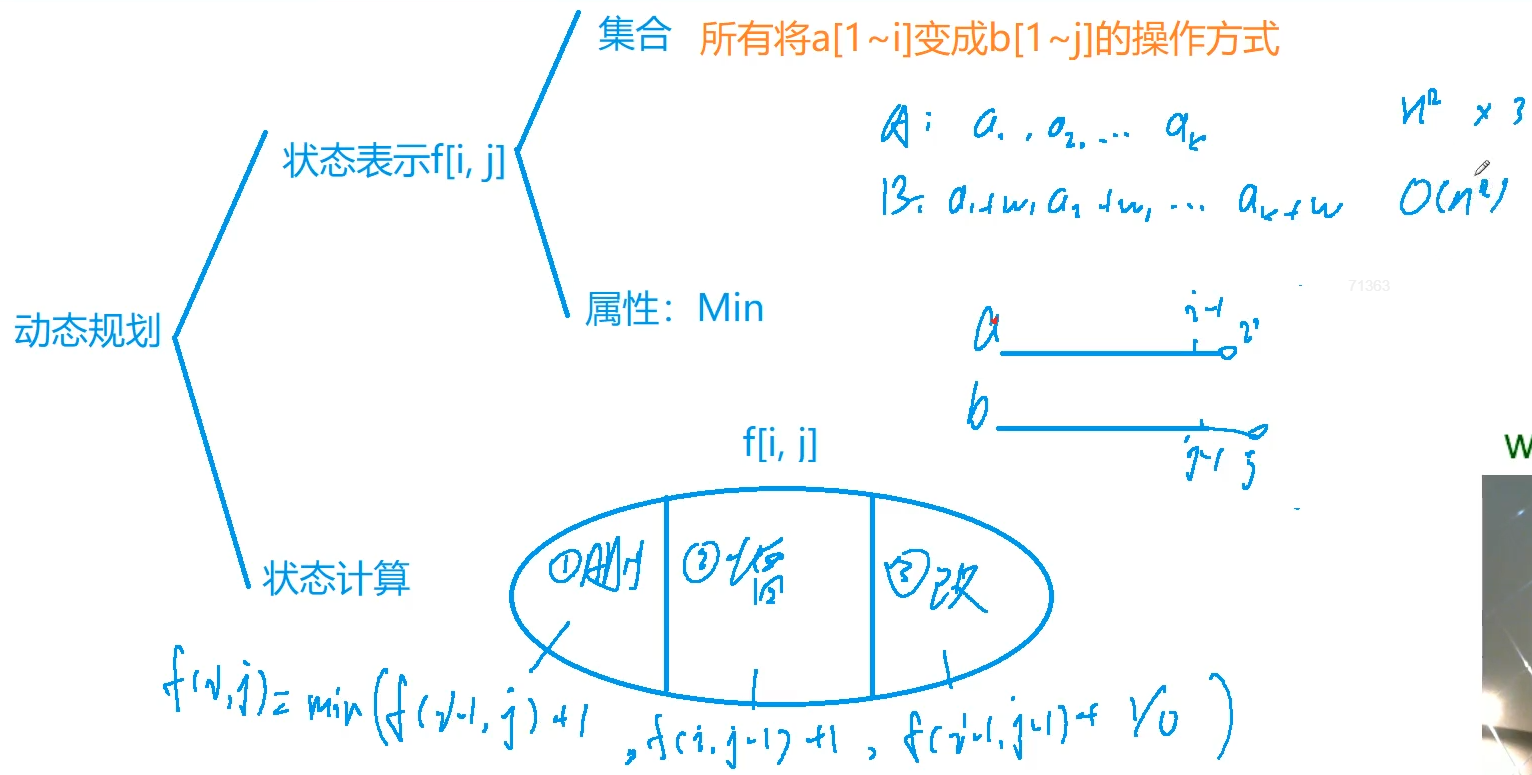
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1005;
char a[N],b[N];
int f[N][N];//a串前i个字母通过变换操作变成b串前j个字母的最小操作次数
int n,m;
int main()
{
cin>>n>>a+1;
cin>>m>>b+1;
//初始化操作,处理边界问题
for(int i = 1;i <= n;i++)
{
f[i][0] = i; //把a串中前i个字母变成0,需要i次删除操作
}
for(int i = 1;i <= m;i++)
{
f[0][i] = i;//把a串中空字串变成b中前i个字母,需要i次添加操作
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
f[i][j] = min(f[i-1][j] + 1,f[i][j-1] + 1); //左边表示删除操作,前提是a[1~i-1]等于b[1~j];
//右边表示添加操作,前提是a[1~i]等于b[1~j-1]
if(a[i] == b[j]) f[i][j] = min(f[i][j],f[i-1][j-1]);//相等不需要替换,前提是a[1~i-1]等于b[1~j-1]
else f[i][j] = min(f[i][j],f[i-1][j-1] + 1); //不相等需要替换操作,前提是a[1~i-1]等于b[1~j-1]
}
}
cout<<f[n][m]<<endl;
return 0;
}
897. 最长公共子序列
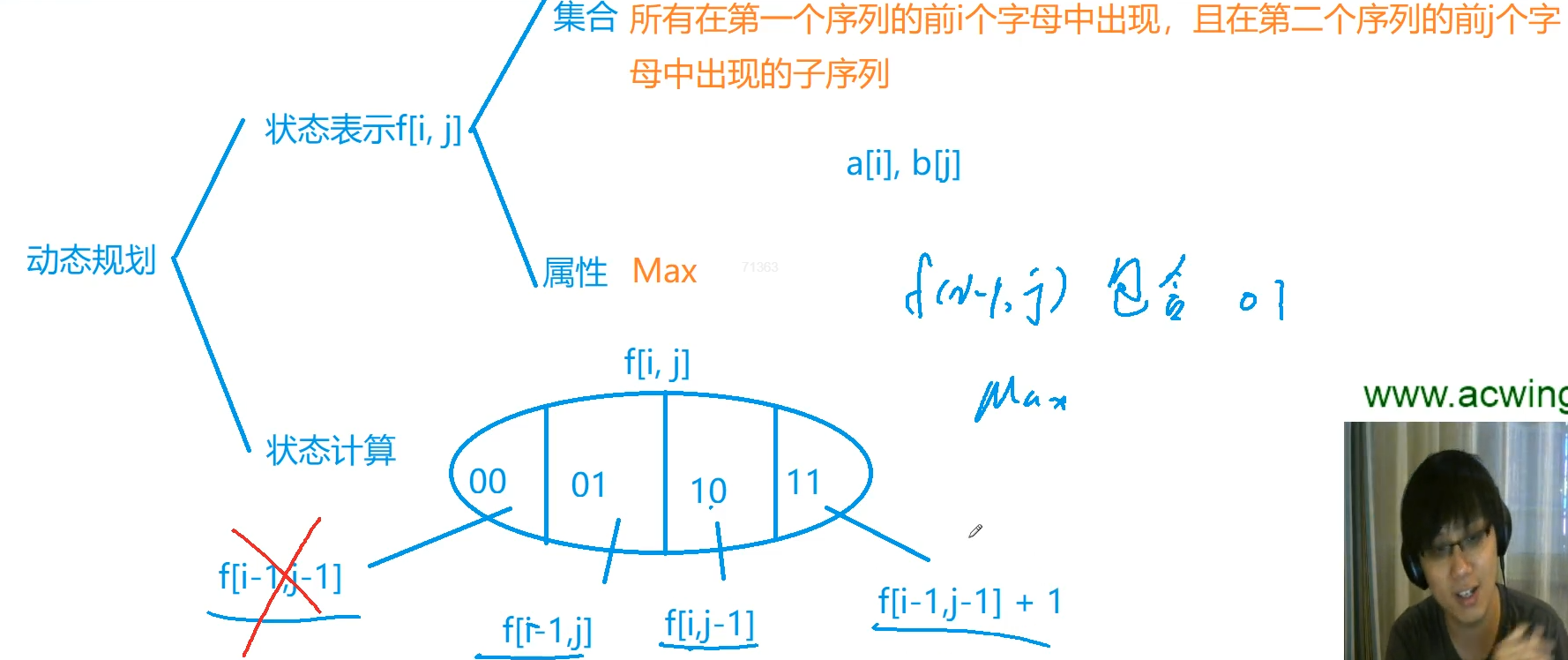

如果两个字符相等,就可以直接转移到f[i-1][j-1],不相等的话,两个字符一定有一个可以抛弃,可以对f[i-1][j],f[i][j-1]两种状态取max来转移。
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1005;
char a[N],b[N];
int n,m;
int f[N][N]; //集合表示:第一个串的前i个字母中,第二个串的前j个字母中的公共子序列,属性:序列长度的最大值
int main()
{
cin>>n>>m;
scanf("%s%s",a+1,b+1);
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= m;j++)
{
if(a[i] == b[j]) //第1个串的第i个字母与第二个串的第j个字母相等,就可以直接转移到f[i-1][j-1]
{
f[i][j] = max(f[i][j],f[i-1][j-1] + 1);
} //不相等的话,两个字符一定有一个可以抛弃,可以对f[i-1][j],f[i][j-1]两种状态取max来转移。
else f[i][j] = max(f[i][j-1],f[i-1][j]);
}
}
cout<<f[n][m]<<endl;
return 0;
}
六、区间DP
思路
f[i,j]表示将第i堆到第j堆所有合并成一堆的最小代价
状态计算:所有第i堆到第j堆合并成一堆的合并方式分成若干类,以最后一步合并的分界线
左边的最小代价+右边的最小代价+最后一步的代价
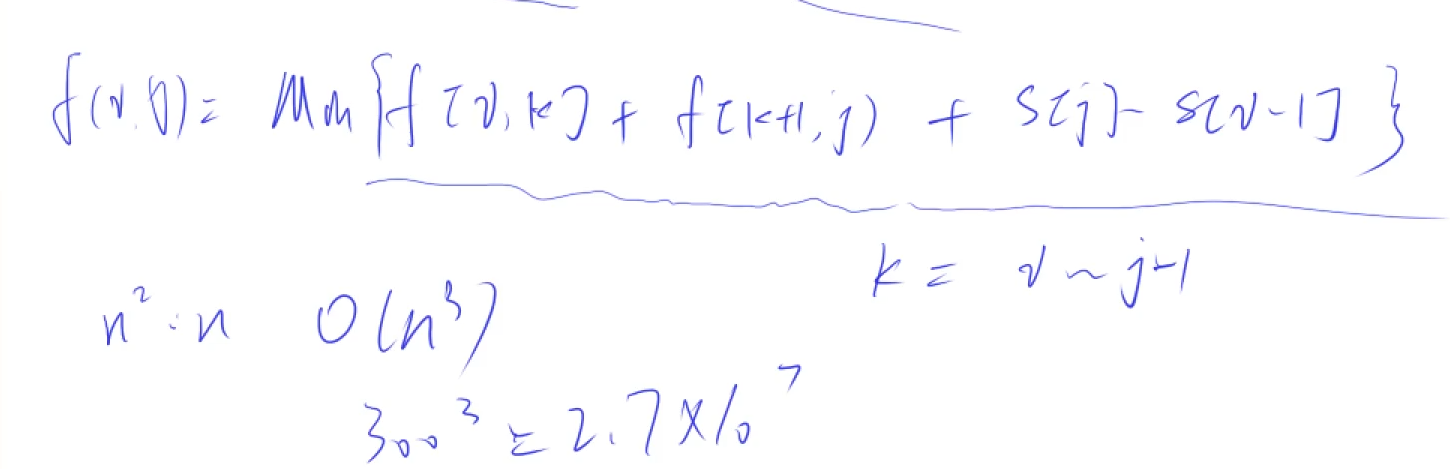
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 305,INF = 0x3f3f3f3f;
int f[N][N],a[N],s[N];
int n;
int main()
{
cin>>n;
for(int i = 1;i <= n;i++)
{
cin>>a[i];
s[i] = s[i-1] + a[i]; // 计算前缀和
}
//由于状态递推要求计算时已求出子区间的结果,因此必须外层从小到大枚举区间长度
for(int len = 2;len <= n;len++) //区间长度为1时,不需要合并,代价为0,故长度从2开始枚举
{
for(int i = 1;i + len - 1 <= n;i++)
{
int l = i, r = i + len - 1;//左右边界
f[l][r] = INF;//计算最小值,故初始化f[l][r]必须为无穷大
for(int k = l;k < r;k++) //分界点枚举 [l,r-1]
{
f[l][r] = min(f[l][r],f[l][k] + f[k+1][r] + s[r] - s[l-1]);
}
}
}
cout<<f[1][n]<<endl;
return 0;
}
七、数位统计DP
338. 计数问题
count(n,x):1-n中x出现的次数
从a到b中x出现的总次数 = count(b,x) - count(a-1,x)
分类讨论

# include <iostream>
# include <cmath>
using namespace std;
int dgt(int n) // 计算整数n有多少位
{
int res = 0;
while (n) ++ res, n /= 10;
return res;
}
int cnt(int n, int i) // 计算从1到n的整数中数字i出现多少次
{
int res = 0, d = dgt(n);
for (int j = 1; j <= d; ++ j) // 从右到左第j位上数字i出现多少次
{
// l和r是第j位左边和右边的整数 (视频中的abc和efg); dj是第j位的数字
int p = pow(10, j - 1), l = n / p / 10, r = n % p, dj = n / p % 10;
// 计算第j位左边的整数小于l (视频中xxx = 000 ~ abc - 1)的情况
if (i) res += l * p;
if (!i && l) res += (l - 1) * p; // 如果i = 0, 左边高位不能全为0(视频中xxx = 001 ~ abc - 1)
// 计算第j位左边的整数等于l (视频中xxx = abc)的情况
if ( (dj > i) && (i || l) ) res += p;
if ( (dj == i) && (i || l) ) res += r + 1;
}
return res;
}
int main()
{
int a, b;
while (cin >> a >> b , a)
{
if (a > b) swap(a, b);
for (int i = 0; i <= 9; ++ i) cout << cnt(b, i) - cnt(a - 1, i) << ' ';
cout << endl;
}
return 0;
}
八、状态压缩DP
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=20,M=1<<N;
int f[M][N],w[N][N];//w表示的是无权图
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
cin>>w[i][j];
memset(f,0x3f,sizeof(f));//因为要求最小值,所以初始化为无穷大
f[1][0]=0;//因为零是起点,所以f[1][0]=0;
for(int i=0;i<1<<n;i++)//i表示所有的情况
for(int j=0;j<n;j++)//j表示走到哪一个点
if(i>>j&1)
for(int k=0;k<n;k++)//k表示走到j这个点之前,以k为终点的最短距离
if(i>>k&1)
f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j]);//更新最短距离
cout<<f[(1<<n)-1][n-1]<<endl;//表示所有点都走过了,且终点是n-1的最短距离
//位运算的优先级低于'+'-'所以有必要的情况下要打括号
return 0;
}
九、树形DP
285. 没有上司的舞会


每个人只有两种状态,则设dp[0][i]dp[0][i]为第i个人不来,他的下属所能获得的最大快乐值;
dp[1][i]dp[1][i]为第i个人来,他的下属所能获得的最大快乐值。
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 6010;
int happy[N];
int h[N],e[N],ne[N],idx;
int f[N][2];
int n;
bool has_father[N]; //有无父节点
void add(int a,int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
void dfs(int u)
{
f[u][1] = happy[u]; //此人来,先加上他本身的快乐值
for(int i = h[u];i!=-1;i=ne[i])
{
int j = e[i];
dfs(j);
f[u][0] += max(f[j][0],f[j][1]); //此人不来,下属来或不来可获得的最大快乐值
f[u][1] += f[j][0]; //此人来,下属就不来
}
}
int main()
{
cin>>n;
for(int i = 1;i <= n;i++)
{
cin>>happy[i];
}
memset(h,-1,sizeof h);
int a,b;
for(int i = 0;i< n-1;i++) //建树
{
cin>>a>>b;
add(b,a);
has_father[a] = true;
}
int root = 1;
while(has_father[root]) root++; //找到根结点
dfs(root);
cout<<max(f[root][0],f[root][1])<<endl; //选根与不选根取较大者
return 0;
}
十、记忆化搜索
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 310;
int h[N][N],f[N][N];
int n,m,res;
int dx[4] = {-1,1,0,0};
int dy[4] = {0,0,-1,1};
int dp(int x,int y)
{
int &v = f[x][y]; //引用给f[x][y]取别名
if(v!=-1) return v; //发现当前位置已经搜过,则直接返回
v = 1;//初始化,最少步数为1
for(int i = 0;i < 4;i++)
{
int a = x + dx[i];
int b = y + dy[i];
if(a>=0 && a<n && b>=0 && b<m && h[x][y] > h[a][b]) //符合要求就尝试搜索
{
v = max(v,dp(a,b) + 1);//切记:此处必须dp进行搜索,不可用f[i][j]
}
}
return v; //搜索完毕一定要返回f[x][y]
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
cin>>h[i][j];
}
}
memset(f,-1,sizeof f); //记忆化搜索,表示未被搜索过
for(int i = 0;i < n;i++)
{
for(int j = 0;j < m;j++)
{
res = max(res,dp(i,j)); //切记:此处必须dp进行搜索,不可用f[i][j]
}
}
cout<<res<<endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号