C语言春考高频考题与常用算法
代码以实现核心功能的算法为主,可能会缺少个别变量的定义和输入(赋值)
考点0:编程规范
-
1.文件命名
-
文件名应具有描述性,使用小写字母,多个单词之间可用下划线 _ 分隔。例如,
calculate_average.c能清晰表明该文件与计算平均值相关 -
头文件使用
.h扩展名,源文件使用.c扩展名
-
-
2.注释规范
- 文件注释:在每个源文件和头文件开头添加注释,说明文件的用途、作者、创建日期和修改记录等信息
/* * 文件名称: calculate_average.c * 文件用途: 此文件包含计算平均值的函数 * 作者: pycoder * 创建日期: 2025-05-07 22:24 * 修改记录: * [修改日期] - [修改人] - [修改内容] */- 函数注释:在每个函数定义前添加注释,描述函数的功能、参数、返回值和可能的异常情况
/** * @brief 计算数组元素的平均值 * @param arr 输入的整数数组 * @param size 数组的大小 * @return 数组元素的平均值 */ double calculate_average(int arr[], int size) { // 函数实现代码 }- 行注释:在每个源文件和头文件开头添加注释,说明文件的用途、作者、创建日期和修改记录等信息
// 计算数组元素的总和 int sum = 0; for (int i = 0; i < size; i++) { sum += arr[i]; } -
3.代码缩进与空格
- 缩进:使用 4 个空格进行缩进,避免使用制表符(Tab),以保证在不同编辑器中代码格式一致
if(condition) { // 条件成立时执行的代码 statement; }- 空格
- 在运算符两边添加空格,增强代码可读性。如
a = b + c;比a=b+c;更易阅读 - 在逗号、分号后添加空格,如
int a, b, c; for(i = 0; i <= 5; i++) - 函数调用时,参数列表中的逗号后添加空格,如
func(arg1, arg2);
- 在运算符两边添加空格,增强代码可读性。如
-
4.变量与常量命名
-
变量命名
-
建议变量定义完后接着赋初值,不要使用没有值的变量
-
变量名应具有描述性,使用小写字母,多个单词之间用下划线分隔。例如,
student_age能明确表示该变量存储学生的年龄 -
避免使用单个字符作为变量名,除非是在简单的循环中,如
for (int i = 0; i < n; i++)中的i
// i j k 常用于循环结构的循环变量 a, s, arr, array 常用于数组名(整型、字符型) temp 数据交换时的临时变量 // tag flag 标志变量,通常取值0或1,根据取值执行不同的数据流 alpha_flag 字母标志变量 num_flag 数字标志变量 // number num n data digit 数据 sum 存放累加的和 multy 存放累积的和 alpha 字母 upper 大写 lower 小写 word 单词 // bin 二进制 oct 八进制 dec 十进制 hex 十六进制 length 长度 count cnt 计数 odd 奇数 even 偶数 // index 索引,下标 ROWS 数组的行数 COLS 数组的列数 min 最小值 max 最大值 min_i 最小值的行标 // min_j 最小值的列标 max_i 最大值的行标 max_j 最大值的列标 avg average 平均数 fac 阶乘 ret result 结果 // day 天 天数 year 年 month 月 price 价格 money pay 支付金额 discount 折扣 h height 身高 employee 员工 // salary 薪水 triangle 三角形 time 时间 store 商店 amount total 总量 score grade 成绩 course 课程 // ch 字符 birth 出生日期 age 年龄 input 输入 print 打印 username 用户名 pwd password 密码 weight 重量 // below 低于 小于 pos positive 正数 neg negative 负数 reverse 置反 反向 d 直径 r 半径 S area 面积 // page 页数 distance 距离 mid 中间位置 中位数 temperature tem 温度 rate 比率 百分比 step 步数 // div 除法 除数 operator 操作符 运算符 use 使用 error 报错 -
-
常量命名
-
常量名使用全大写字母,多个单词之间用下划线分隔。例如,
MAX_SIZE表示最大尺寸 -
定义常量时,使用
const关键字,如const int MAX_SIZE = 100;
-
-
-
5.函数规范
-
函数长度:单个函数的代码长度不宜过长,一般控制在 50 - 100 行以内。若函数功能复杂,可将其拆分为多个小函数
-
函数参数:函数参数不宜过多,一般不超过 5 个。若参数过多,可考虑使用结构体封装参数
-
函数返回值:函数应明确返回值的含义,避免返回无意义的值。若函数无返回值,应使用
void类型
-
-
6.控制结构规范
if - else语句:即使if或else语句块中只有一条语句,也建议使用花括号{}括起来,避免代码歧义
if (condition) { statement; } else { statement; }- 循环语句:循环条件应清晰明确,避免出现无限循环的情况;循环体中避免进行复杂的计算和操作,可将其封装为函数
-
7.错误处理与异常情况
-
错误返回值:函数在出现错误时,应返回特定的错误码,便于调用者进行错误处理。例如,若函数返回
-1表示出现错误 -
异常处理:在可能出现异常的地方添加错误检查代码,如文件打开失败、内存分配失败等情况
FILE *fp = fopen("file.txt", "r"); if (fp == NULL) { // 处理文件打开失败的情况 perror("文件打开失败"); return -1; } -
-
8.代码复用与模块化
-
模块化设计:将功能相关的代码封装成函数或模块,提高代码的复用性和可维护性。例如,将字符串处理功能封装成一个模块,包含字符串拼接、查找等函数
-
避免代码重复:若有重复的代码逻辑,应将其提取为函数,避免代码冗余
-
-
9.代码可读性与可维护性
- 避免使用复杂的表达式:尽量将复杂的表达式拆分成多个简单的语句,提高代码的可读性
// 复杂表达式 int result = (a + b) * (c - d) / e; // 拆分成多个简单语句 int sum = a + b; int diff = c - d; int product = sum * diff; int result = product / e;- 使用有意义的宏:宏定义应具有明确的含义,避免使用过于复杂的宏。例如,
#define PI 3.14159能清晰表示圆周率
考点1:多位数拆分性质探索
- 1.简单的多位数拆分(以4位数为例)
// 掌握个位、十位、百位和千位的拆分方法
// 程序中用于处理的数字通常定义为变量num或n,下同
unit = num % 10;
ten = num / 10 % 10;
hundred = num / 100 % 10;
thousand = num / 1000;
// 拆分结束后可基于各位数进行运算
// 输入一个整数n,输出个位、十位和百位加和等于 n 的三位数。例如输入2,输出101、110、200,共3个
for(i = 100; i <= 999; i++){
if(i % 10 + i / 10 % 10 + i / 100 == n){
printf("%d ", i);
}
}
- 2.简单的多位数拆分(以位数不确定的数为例)
// 当位数不确定时,上述逐位分割的方法虽然可行,但比较繁琐,为此可用循环结构实现
while(num){
b = num % 10; // b为拆分出的每一位数
sum = sum + b;
num = num / 10;
}
// 这段循环代码在判断一系列数据的某项特征时很常用,如判断1000以内百位数是5的整数等等
// 应用1:输入一个4位数,计算每一位数平方的和。如输入1234,输出30
while(num){
b = num % 10;
sum += b * b;
num /= 10;
}
printf("sum=%d\n", sum);
// 应用2:输入正整数 n,统计 1 - n 的数中一共出现了多少次 8(2025年网络技术技能真题)
int cal_eight(int n){
int i, data, a, count = 0;
for(i = 1; i <= n; i++){
data = i;
while(data) {
a = data % 10;
if(a == 8){
count++;
}
data /= 10;
}
}
return count;
}
- 3.奇偶性判断
// 本质上是 num 能否被2整除
num % 2 == 0 // num为偶数
num % 2 != 0 // num为奇数
if(num % 2) {
exp; // 在num为奇数的时候才会执行
}
// 引申1:a能被b整除
a%b == 0
// 引申2:a能整除b
b%a == 0
- 4.和、积、计数
sum = 0;
multy = 1;
count = 0;
考点2:选择语句的基础应用
- 1.两个数排序(最大、最小值)
if (a > b) {
temp = a;
a = b;
b = temp;
}
- 2.三个数排序(最大、最小值)
if(a > b) {
temp = a;
a = b;
b = temp;
}
if(a > c) {
temp = a;
a = c;
c = temp;
}
if(b > c) {
temp = b;
b = c;
c = temp;
}
max = (max = a < b ? b : a) < c ? c : max;
// 超过3个数的排序不建议使用这种方法,可直接使用排序算法(后文介绍)
// 情况分类很多时使用 switch 语句,如月份与春夏秋冬、周一到周日
- 3.分段函数
// 注意 if 多分支语句中隐含的条件,涉及到数学函数的分段函数
// 当x < 1时, y = x;当1 ≤ x < 10时,y = 2x - 1
if (x < 1) {
y = x;
}
else if (x < 10) { //隐含条件:x >= 1
y = 2 * x -1;
}
// 简单应用题:阶梯打车费、阶梯电费、阶梯水费等,应用题自变量的值通常不低于0,做题时要考虑到输入非法的情况
// 月用电量不高于 50 千瓦时电价为 0.55 元/千瓦时,超过 50 千瓦时,超出部分的用电量电价上调0.05元/千瓦时
if(x >= 0 && x <= 50) {
y = 0.55 * x;
}
else {
y = 0.6 * x - 2.5;
}
- 4.不低于3种的选择(以春夏秋冬 点餐系统选择为例)
// 基于switch语句实现
// 4.1 假设3-5月是春天,6-8月是夏天,9-11月是秋天,12-2月是冬天。输入月份,输出对应的季度
switch(month) {
case 3:
case 4:
case 5: printf("春天"); break;
case 6:
case 7:
case 8: printf("夏天"); break;
case 9:
case 10:
case 11: printf("秋天"); break;
case 12:
case 1:
case 2: printf("冬天"); break;
default: printf("月份错误!"); break;
}
// 4.2 假设点餐系统中,输入0打印"正在查看菜单…",输入1打印"开始点餐…",输入2打印"正在查看购物车…",输入3打印"正在结账…",输入4打印
// "退出点餐系统…",其他输入则会提示"功能选项输入错误,请重新输入! "
switch(op) {
case 0: printf("正在查看菜单...\n"); break;
case 1: printf("开始点餐...\n"); break;
case 2: printf("正在查看购物车...\n"); break;
case 3: printf("正在结账...\n"); break;
case 4: printf("退出点餐系统...\n"); exit(-1);
default: printf("功能选项输入错误,请重新输入!\n"); break;
}
// 4.3 有的题目中分类情况比较复杂,可以借助数学运算转化为"等级变量"(程序填空题居多),如折扣、成绩等
// 应用1:成绩90-100为A,80-89为B,70-79为C
r = score/10;
switch(r) {
case 10:
case 9: printf("A"); break;
case 8: printf("B"); break;
case 7: printf("C"); break;
default: printf("D"); break;
}
// 应用2:消费未满500元无折扣,满500元打9折,满1000元打8折,满2000元打7折
if (money >= 2000) {
grade = 4;
}
else {
grade = money/500;
}
switch(grade) {
case 0: c = 1; break;
case 1: c = 0.9;break;
case 2:
case 3: c = 0.8; break;
case 4: c = 0.7; break;
}
pay = c * money;
// 4.4 有的题目中各等级的运算相互叠加与影响,如个人所得税、奖金提成等
// 利润不高于 10 0000,奖金提成10%;不高于 20 0000,低于 10 0000的部分10%提成,高于10 0000的部分提成7.5%;不高于40 0000,低于20 0000的
// 部分仍按上述办法提成(下同),高于20 0000的部分提成5%;不低于60 0000时,高于40 0000的提成3%;不低于100 0000时,高于60 0000的部分提成1.5%;
// 高于100 0000时超过1000000的部分提成1%
bon1 = 100000 * 0.1; // 利润达到10 0000元的提成
bon2 = bon1 + 100000 * 0.075; // 利润达到20 0000元的提成
bon4 = bon2 + 200000 * 0.05; // 利润达到40 0000元的提成
bon6 = bon4 + 200000 * 0.03; // 利润达到60 0000元的提成
bon10 = bon6 + 400000 * 0.015; // 利润达到100 0000元的提成
branch = i / 100000; // 变量 i 为利润值
if(branch > 10) {
branch = 10;
}
switch(branch) {
case 0: bonus = i * 0.1; break;
case 1: bonus = bon1 + (i - 100000) * 0.075; break;
case 2:
case 3: bonus = bon2 + (i - 20000) * 0.05; break;
case 4:
case 5: bonus = bon4 + (i - 400000) * 0.03; break;
case 6:
case 7:
case 8:
case 9: bonus = bon6 + (i - 600000) * 0.015; break;
case 10: bonus = bon10 + (i - 1000000) * 0.1;
}
// 4.5 若switch中匹配后的操作比较复杂,可以封装为函数进行处理,如考点13
- 5.数学知识补充
// 构成三角形的条件
a + b > c && a + c > b && b + c > a
// 直角三角形
a * a + b * b == c * c || b * b + c * c == a * a || a * a + c * c == b * b
// 折扣问题
price * 0.8 // 打8折
price * 0.2 // 优惠8折
// 三角形面积
s = sqrt(p * (p-a) * (p-b) * (p-c)),其中p = (a + b + c) / 2,注意整除问题!
s = 1.0 / 2 * a * b * sin(alpah),alpha为边a、b的夹角
// 余弦定理
c^2 = a^2 + b^2 - 2abcos(alpha),alpha为边a、b的夹角
// 判断闰年:能被4整除但不能被100整除或者能被400整除
year % 4 == 0 && year % 100 != 0 || year % 400 == 0
// 杨辉三角:除第一列和对角线全为1外,其余元素值为左斜上方与正上方元素之和
a[i][0] = 1, a[i][i] = 1;
a[i][j] = a[i - 1][j - 1] + a[i - 1][j];
// 利息计算公式:若存款额为 p0,活期年利率为 r1,一年定期年利率为 r2,存两次半年期年利率为r3。按以上3种方式存款 1 年后的本息和分别为:p1 = p0 * (1 + r1),p2 = p0 * (1 + r2),p3 = p0 * (1 + r3/2) * (1 + r3/2)
// 若年利率为r,n为存款年数,则n年期本息和为 pn = p0 * (1 + n * r);存n次1年期的本息和为pn = p0 * (1 + r)^n;一个季度的本息和pn = p0 * (1 + r / 4)
考点3:融合循环的数理运算
- 1.计算阶乘
// 非递归版
result = 1;
for(i = 1; i <= num; i++) {
result *= i;
}
// 递归版
float fac(int n) {
if (num <= 1) {
return 1;
}
else {
return fac(n - 1);
}
}
// 阶乘变形:计算1- 1/3! + 1/5! - 1/7! + ...的和,直到某一项的绝对值小于0.0001
// 累加、累乘等算式中,每一项的值通常用变量 term 表示
int t = 1, i = 1;
float term = 1.0/i, sum = 0;
while(fabs(term) >= 0.0001) {
sum += term;
i += 2;
t = -t;
term = 1.0/fac(i)*t;
}
printf("term=%f, sum=%f\n", term, sum);
- 2.计算斐波那契数列
// 方法1:非递归版(迭代)
int f1 = 1, f2 = 1, f3;
while(1){
f3 = f1 + f2;
printf("%4d", f3);
f1 = f2;
f2 = f3;
}
// 方法2:递归版
int fib(int n) {
if(n <= 2) {
return 1;
}
else {
return fib(n - 1) + fib(n - 2);
}
}
// 斐波那契数列变形:2/1 + 3/2 + 5/3 + 8/5 + ...
int f1 = 1, f2 = 2, f3, i;
float sum = 0, term;
for(i = 1; i <= 20; i++) {
f3 = f1 + f2;
term = f2 * 1.0 / f1; // 注意整数相除时结果为整数的情况,可乘以 1.0 转为浮点数
sum += term;
f1 = f2;
f2 = f3;
}
- 3.项数确定且子项同正(或同负)的算式运算(以 1 + 3 + 5 + ... + 199 为例)
int sum = 0;
for(i = 1; i < 200; i += 2) {
sum += i;
}
- 4.项数确定且子项正负相间的算式运算(以 1 - 2 + 3 - 4 + 5 - 6 + 7 - 8 为例)
// 方法1:使用标志变量
int t = 1, sum = 0; // 用作标志变量,控制正负号交替出现
for(i = 1; i <= 8; i++) {
sum = sum + i * t;
t = -t;
}
// 方法2:结合奇偶性
int sum = 0;
for(i = 1; i <= 8; i++) {
if(i % 2) {
sum = sum + i;
}
else {
sum = sum - i;
}
}
- 5.形如 n + nn + nnn + nnnn 的算式运算
// 将 nn 看做 n * 10 + n,nnn 看做 nn * 10 + n
int sum = 0, t = n; // t中暂存n的初值,后续基于t运算求nn、nnn等
for(i = 1; i <= 4; i++){
sum = sum + t;
t = t * 10 + n;
}
- 6.项数不确定的算式运算(直到用户输入...为止 直到某项小于...为止)
// 6.1 持续输入数据直到0为止
while(num != 0){
sum += num;
printf("请继续输入一个整数, 直到0停止: ");
scanf("%d", &num);
}
// 6.2 等比数列模型:1mm的纸对折多少次能超过1.5m的厚度(公比为2)
h1 = 1500, h2 = 1, count = 0;
while (h2 <= h1) {
h2 *= 2;
count++;
}
// 6.3 等差数列模型:共 160 页的书,第一天读 10 页,以后每天比前一天多读 5 页,几天读完,最后一天读多少页(公差为 5)
// days: 总天数 pages_everyday: 每天读的页数 pages_total: 读过的总页数 pages_lastday: 最后一天读的页数
int days = 1, pages_everyday = 10, pages_total = 10, pages_lastday;
while(pages_total <= 160){
pages_everyday += 5;
pages_total += pages_everyday;
days++;
}
pages_lastday = 160 - (pages_total - pages_everyday);
// 6.4 计算 1 + 1/2 + 1/4 + 1/8 + 1/16 + …的值,直到最后一项值小于0.0001
// 涉及分数计算时,注意C语言中整数除法结果仍为整数导致的结果不准确
float t = 1.0;
double sum = 0;
while(t >= 0.0001) {
sum += t;
t = t / 2; // 注意将t定义成浮点型,如果是整型的话 t / 2 结果为整数,计算结果不准确
}
// 6.5 输入温度,直到输入0为止,计算最高温和高温(大于38摄氏度)比例
// 输出百分号要用%%;计算比例时两整数相除要乘以1.0后做除法,或分子分母一方强制转换为 float型
// count表示高温的个数,total表示温度总的个数,初值均为0
float temperature, rate;
while(temperature != 0){
if(temperature > 38){
count++;
}
scanf("%f", &temperature);
total++;
}
total++; // 将最后输入的0摄氏度加上
rate = (count * 1.0 / total) * 100;
// rate = (float)count / total * 100;
printf("总共输入了 %d 个温度, 其中高温占了 %d 个, 占比为 %.2f%%", total, count, rate);
- 7.估算圆周率 π 的值
// 公式1:(π*π)/6 = 1 + 1/(2*2) + 1/(3*3) + ... + 1/(n*n)
for(i = 1; i <= n; i++) { // n的值应当足够大,求得的值才更接近 π
s = s + 1.0/(i*i); // 注意:1/(i*i)为1或0
}
s = sqrt(6*s);
// 公式2:π/4 = 1 - 1/3 + 1/5 - 1/7 + ... 直到某一项的绝对值小于0.000001
int i = 1, sign = 1; // ±1 交替的变量可用sign表示
double sum = 0, item = 1.0 / i;
while (fabs(item) >= 1e-6) {
sum = sum + item * sign;
sign = -sign;
i += 2;
item = 1.0 / i;
}
- 8.裂项:整数的 N 项加和分解问题
// 找到多组连续的整数,这些整数相加的和为num,输出项数最多的一组连续整数
// 如 3 + 4 + 5 + 6 + 7 + 8 + 9 + 1 0 + 11 + 12 + 13 + 14 = 102,24 + 25 + 26 + 27 = 102, 33 + 34 + 35 = 102
int flag = 0, mid = num / 2; // 当只有连续的两个数相加时,这两个数在中间附近,如51 + 52 = 103
for(i = 1; i <= mid; i ++){ // 所以 i 最高取到 mid,如 103 的加数 51
sum = i;
for(j = i + 1; j <= mid + 1; j++){ // j 最高取到 mid + 1,如 103 的加数 52
sum += j;
if(sum == num){
flag = 1;
for(k = i; k <= j; k++){
printf("%d ", k);
}
break;
}
}
if(flag){ // i 从小开始遍历,最先找到的一组加数一定是最多的一组,只要找到一组输出后直接返回
break;
}
}
if(!flag) {
printf("无法分解");
}
- 9.完数:因子之和等于这个数,如 6 = 1 + 2 + 3
for (num = 1; num <= 1000; num++) {
sum = 0;
for (i = 1; i <= num/2; i++) {
if (num % i == 0) {
sum += i;
}
}
if(sum == num){
printf("%d ", num);
printf("its factors are ");
for (i = 1; i <= num / 2; i++) {
if (num % i == 0) {
printf("%d ", i);
}
}
printf("\n");
}
}
- 10.求最大公约数与最小公倍数
multy = m * n;
if (m < n) {
temp = m;
m = n;
n = temp;
}
do {
r = m % n;
m = n;
n = r;
} while(r);
printf("最大公约数为: %d 最小公倍数为: %d\n", m, multy / m);
- 11.倒序递推问题(以猴子吃桃为例)
// 猴子第1天摘下若干个桃子,吃了一半,又多吃了1个。第2天又将剩下的桃子吃了一半,又多吃了1个。以后每天都吃了前一天剩下的一半零1个。到第10天早上再想吃桃子时只剩下1个了,求第1天共摘了多少个桃子
// 递推公式:n(10) = 1 n(9) = 2 * (n(10) + 1) n(8) = 2 * (n(9) + 1) ... n(t) = 2 * (n(t - 1) + 1)
int i, num = 1;
for (i = 9; i >= 1; i--) {
num = 2 * (num + 1);
}
day = 9;
x2 = 1;
while(day > 0) {
x1 = (x2 + 1) * 2;
x2 = x1;
day--;
}
考点4:融合整型数组的数理运算
- 1.基础:一维数组与二维数组(矩阵)的输入输出
// 必须掌握,后续计算整体平均值、行列平均值、数组特性探索等都要基于数组的遍历
for (i = 0; i < ROW; i++) {
scanf("%d", &array[i]);
}
for (i = 0; i < ROW; i++) {
scanf("%d", array + i);
}
for (i = 0; i < ROW; i++) {
printf("%-4d", array[i]);
}
for (i = 0; i < ROW; i++) {
for (j = 0; j < COL; j++) {
scanf("%d", &array[i][j]);
}
}
for (i = 0; i < ROW; i++) {
for (j = 0; j < COL; j++) {
scanf("%d", array[i] + j);
}
}
for (i = 0; i < ROW; i++) {
for (j = 0; j < COL; j++) {
printf("%-4d", array[i][j]);
}
printf("\n");
}
// 了解:动态数组的申请与释放,malloc与free函数
// malloc 函数用于分配指定大小的内存块,其原型为 void* malloc(size_t size); size 为需要分配的内存字节数,若分配成功,返回指向分配内存块起始地址的指针;若失败,返回 NULL
// 使用完动态分配的内存后,必须调用 free 函数释放内存,以避免内存泄漏。free 函数的原型为 void free(void* ptr); ptr 是之前分配内存块的指针。
// 注意:free 只能释放通过 malloc、calloc 或 realloc 分配的内存,且每个分配的内存块只能释放一次。释放后,指针变为悬空指针,若需要继续使用,应重新分配内存
#include <stdio.h>
#include <stdlib.h>
int main() {
int n = 5;
// 申请能存放 n 个 int 类型元素的动态数组
int *arr = (int*)malloc(n * sizeof(int));
if (arr == NULL) {
printf("内存分配失败\n");
return 1;
}
// 使用动态数组
for (int i = 0; i < n; i++) {
arr[i] = i;
}
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
// 释放动态数组
free(arr);
return 0;
}
// 理解:可变长数组VLA
// 在 C99 (1999年发布)及之后的标准里,支持可变长度数组,能够使用变量来指定数组的长度。1989年发布的C89/C90标准不支持VLA,以下代码可能会报错
int i, n, min;
printf("请输入n的值:");
scanf("%d", &n);
int arr[n];
for(i = 0; i < n; i++){
printf("请输入第%d个数:", i + 1);
scanf("%d", arr+i);
}
// 在C89/C90标准下不可使用可变长度数组时,能够借助动态内存分配函数像malloc、calloc或者realloc)来创建数组,具体方法在上文已介绍
- 2.计算数组中元素的和与平均值
// 2.1 计算正数的平均值
float avg = 0.0f;
int count = 0;
for(i = 0; i < 10; i++) {
if(a[i] > 0) {
avg += a[i];
count++;
}
}
avg /= count;
// 若数据通过键盘输入,可以边输入边计算,减少代码量
for(i = 0; i < 10; i++){
// scanf("%f", a + i);
scanf("%f", &a[i]);
sum += a[i];
}
avg = sum/10;
// 2.2 计算每行元素的平均值
for(i = 0;i < 3; i++){
avg[i] = 0; // 数组 avg 存储各行元素的平均值
for(j = 0; j < 4; j++){
scanf("%d", &a[i][j]);
avg[i] += a[i][j];
}
avg[i] /= 4;
printf("第 %d 行的平均值为 %f ", i + 1, avg[i]);
}
// 2.3 计算每列元素的平均值
for (j = 0; j < COLS; j++) {
sum = 0; // 每当新的一列开始时,先将和置为 0
for (i = 0; i < ROWS; i++) {
sum += arr[i][j];
}
averages[j] = (double)sum / ROWS;
}
// 2.4 查找最接近平均值且不大于(<=)平均值的数
int closest_num = 0;
double min_diff = 1e9; // 假设刚开始的平均值与不大于平均值的元素的差值无穷大,初次测试就能更新为更小的
average = (double)sum / NUM_COUNT; // 计算出所有数的平均值
for (i = 0; i < NUM_COUNT; i++) {
if (numbers[i] <= average) { // 找到了一个小于平均值的数
diff = average - numbers[i]; // 计算平均值和当前数的差
if (diff < min_diff) { // 比较现有差值和最小差值
min_diff = diff;
closest_num = numbers[i];
}
}
}
printf("最接近且不大于平均值的数是: %d\n", closest_num);
// 2.5 查找高于平均成绩的学生的平均成绩
avg1 /= 6;
count = 0;
for(i = 0; i < 6; i++) {
if(score[i] > avg1) {
avg2 += score[i];
count++;
}
}
avg2 /= count;
// 应用1:数组元素特征初始化。现有一个5 行 5 列的二维数组,第 5 行和第 5 列元素均未初始化,其余元素均为0或1。若每行 1 的个数为偶数则该行第 5 个数初始化为 1,反之为 0;若每列 1 的个数是偶数则该列第 5 个数初始化为1,反之为0。
for (i = 0; i < ROW - 1; i++) {
sum = 0; // 每行数的和初始化为 0
for (j = 0; j < COL - 1; j++) {
sum += a[i][j];
}
// 程序执行到这个地方时,算出了下标为 i 的行的 4 个数之和
if (!(sum%2)) {
a[i][j] = 1; // 初始化本行第 5 个数
}
}
for (j = 0; j < COL; j++) {
sum = 0; // 每列数的和初始化为 0
for (i = 0; i < ROW - 1; i++) {
sum += a[i][j];
}
// 程序执行到这个地方时,算出了下标为 j 的列的 4 个数之和
if (!(sum%2)) {
a[i][j] = 1; // 初始化本行第 5 个数
}
}
// 应用2:数组元素特征初始化。现有 3 * 4 矩阵,前 3 列元素已知,若每行元素之和为20,求第 4 列元素值
for(i = 0; i < 3; i++){
sum = 0; // 每行数的和初始化为 0
for(j = 0; j < 3; j++){
sum += a[i][j];
}
// 程序执行到这个地方时,算出了下标为 i 的行的 3 个数之和
a[i][3] = 20 - sum; // 计算下标为 i 的行的最后一个数
}
- 3.查找数组元素的最值
// 3.1 面向所有元素的最值及下标
int max, i, j, max_i, max_j;
max = a[0][0];
for (i = 0; i < ROW; i++) {
for (j = 0; j < COL; j++) {
if (a[i][j] > max) {
max = a[i][j];
max_i = i;
max_j = j;
}
}
}
printf("最大值:%d,行号:%d,列号:%d\n", max, max_i, max_j);
int min, i, j, pos[2] = {0};
min = a[0][0];
for (i = 0; i < ROW; i++) {
for (j = 0; j < COL; j++) {
if (a[i][j] < min){
min = a[i][j];
pos[0] = i;
pos[1] = j;
}
}
}
printf("最小值:%d,行号:%d,列号:%d\n", min, pos[0], pos[1]);
// 3.2 面向每一行元素的最值及下标
for (i = 0; i < ROWS; i++) {
// 将每行第 1 列元素置为最值,并标记其列号
maxVal = arr[i][0], maxIndex = 0;
minVal = arr[i][0], minIndex = 0;
for (j = 1; j < COLS; j++) { // 从第 2 列开始遍历
if (arr[i][j] > maxVal) {
maxVal = arr[i][j];
maxIndex = j;
}
if (arr[i][j] < minVal) {
minVal = arr[i][j];
minIndex = j;
}
}
// 程序执行到这个地方时,下标为 i 的行的最值和列号均已求得
printf("第 %d 行的最大值是 %d,下标为 (%d, %d);最小值是 %d,下标为 (%d, %d)\n", i + 1, maxVal, i, maxIndex, minVal, i, minIndex);
}
// 3.3 面向每一列元素的最值及下标
// 应用:有三位同学和每位同学四门课的成绩,求单科最大值,每门课的最大值;有三位运动员和每位运动员五个项目的成绩,求每个项目的最高成绩
// 类似情境要能联想到二维数组
for (j = 0; j < COL; j++) {
max = min = a[0][j]; // 假设该列第 1 个数是最值
// 记录最值的行列标
max_i = min_i = 0;
max_j = min_j = j;
for (i = 1; i < ROW; i++) { // 从每列的第 2 个数开始遍历
if (a[i][j] > max) {
max = a[i][j];
max_i = i;
max_j = j;
}
if (a[i][j] < min) {
min = a[i][j];
min_i = i;
min_j = j;
}
}
}
// 3.4 删除最值,最值后续元素需要往前移动,假设最值的下标为index
while(index <= length-2){ // index最大到length - 2
a[index] = a[index+1];
index++;
}
for(i = 0; i < length-1; i++){ // 前移后的数组长度变为length -1
printf("%d ", a[i]);
}
- 4.构造特殊的矩阵
// 4.1 构造杨辉三角
for(i = 0; i < ROW; i++){
s[i][0] = 1; // 将列标为 0 的元素置为 1
s[i][i] = 1; // 将对角线元素置为 1
}
// 除第一列和对角线元素外,其余元素值为正上方元素与左斜上方元素之和
for(i = 2; i < ROW; i++){ // 前两行元素均为 1,从第 3 行开始遍历
for(j = 1; j < i; j++){ // 每行从第 2 个数开始求值,直到对角线元素前一个
s[i][j] = s[i-1][j] + s[i-1][j-1];
}
}
// 4.2 构造奇数阶魔方阵
// 定义n阶“魔方阵”如下:方阵中的数由1-n^2组成,每个数仅出现一次;每一行、每一列和对角线之和均相等。例如3阶“魔方阵”为{{8, 1, 6}, {3, 5, 7}, {4, 9, 2}},请根据以下算法打印奇数阶(n为奇数)魔方阵。
// 奇数阶“魔方阵”中各数的排列规律如下:1.将 1 放在第 1 行(下标为 0 的行,下同)中间一列;
// 2.从 2 ~ n^2 各数依次按此规则存放:
// 2.1 每一个数存放的行比前一个数的行数减 1,列数加 1;
// 2.2 如果上一个数在第 1 行,则下一个数转到第 n 行(即最下方下标为 n-1 的行);
// 2.3 如果上一个数在第 n 列,则下一个数转到第 1 列,同时行数减1;
// 2.4 如果按上述规则确定的位置上已有数,或上一个数是第1行第n列时,则把下一个数放在上一个数的正下方。
int n, i, j, pre_i, pre_j, k;
int a[MAX][MAX] = {0}; // 矩阵所有元素初始化为 0
i = 0; // 第 1 个数的行标
j = n / 2; // 第 1 个数的列标
a[i][j] = 1; // 存储矩阵的第 1 个元素 1,在第 1 行C位
for (k = 2; k <= n*n; k++) { // 遍历 2~n*n 赋值到特定位置
pre_i = i; // 在计算下一个待存数的行标前, 先存储上一个数的行标
pre_j = j; // 在计算下一个待存数的列标前, 先存储上一个数的列标
i = pre_i - 1; // i 为新数(即将要存入的数)的行标, 缺省情况下在上一个数的前一行
j = pre_j + 1; // j 为新数的列标, 缺省情况下在上一个数的后一列
// 以下代码是针对特殊情况的分析
if (pre_i == 0) { // 情况1: 上一个数在第 1 行, 如 1
i = n - 1; // 将新数的行回到第 n 行
}
if (pre_j == n - 1) { // 情况2: 上一个数在第 n 列
j = 0; // 将新数的列回到第 1 列
}
// 情况3: 按上述所得行列标位置已有数 或 前一个数在第 1 行第 n 列
if (a[i][j] != 0 || (pre_i == 0 && pre_j == n - 1)) {
i = pre_i + 1; // 将新数的行改为前一个数下一行
j = pre_j; // 将新数的列置为前一个数所在列
}
a[i][j] = k; // 分析过所有可能情况后, 找到了要存的行列标, 并将新数 k 存至指定位置
}
- 5.数组元素的交集、并集和差集
// 5.1 查找数组 a 中存在但数组 b 中不存在的数并存入数组 c
for(i = 0; i < length_a; i++){
for(j = 0; j < length_b; j++){
if(a[i] == b[j]){ // 两数组中均存在的数,直接退出遍历 b 的循环
break;
}
}
if(j == length_b){ // 内循环正常结束,即没有在 b 中找到某数
c[k++] = a[i];
}
}
c[k] = '\0';
// 5.2 打印数组 a 和数组 b 中都存在的数
// 检查元素num是否在数组arr中
int isExist(int num, int arr[], int arr_len) {
for (int i = 0; i < arr_len; i++) {
if (arr[i] == num) {
return 1;
}
}
return 0;
}
// 打印两个数组的交集(去重版)
void printIntersection(int a[], int a_len, int b[], int b_len) {
int temp[100]; // 临时存储已找到的交集元素(去重)
int temp_len = 0; // 临时数组有效长度
printf("数组a和数组b的共同元素(去重):");
for (int i = 0; i < a_len; i++) {
// 条件:1.在b中存在 2.未存入临时数组(未打印过)
if (isExist(a[i], b, b_len) && !isExist(a[i], temp, temp_len)) {
temp[temp_len++] = a[i]; // 存入临时数组去重
printf("%d ", a[i]);
}
}
printf("\n");
}
int main() {
int a[] = {1, 2, 3, 3, 4, 5, 6};
int b[] = {3, 5, 7, 8, 3, 9};
int a_len = sizeof(a) / sizeof(a[0]);
int b_len = sizeof(b) / sizeof(b[0]);
printIntersection(a, a_len, b, b_len);
return 0;
}
// 遍历数组a中的数,每确定其中一个数,就去数组b中查找这个数,若b中也存在则输出。但此时应当注意2个问题:
// ①在遍历数组a中当前的数a[i]时,a[i]之前可能出现过a[j]和a[i]相等(j<i),若a[j]刚好在数组b中也存在,此时再基于a[i]去b中查找会导致重复输出;
// ②在遍历数组a中当前的数a[i]时,数组b中可能有多个b[k]与a[i]相等,此时也可能会导致重复输出
for (i = 0; i < LEN1; i++) {
for (j = 0; i >= 1 && j < i; j++) { // i = 0时a[i]前方没有数, 所以加了条件i >= 1
if (a[j] == a[i]) { // a[i] 前方出现过和它相等的 a[j]
break;
}
}
if (j == i) { // a[i] 前方未出现过和它相等的 a[j]
for (k = 0; k < LEN2; k++) {
if (a[i] == b[k]) {
printf("%-4d", a[i]);
break; // 只要找到一个 b[k] 和 a[i] 相等即可
}
}
}
}
// 5.3 计算数组 arr1 和数组 arr2 的并集,结果存储在数组 unionArr 中
int isInArray(int element, int arr[], int size) { // 检查元素是否在数组中的函数
for (int i = 0; i < size; i++) {
if (arr[i] == element) {
return 1;
}
}
return 0;
}
int arr1[MAX_SIZE], arr2[MAX_SIZE], unionArr[MAX_SIZE]; // union有合并、并集的含义
int size1, size2, unionSize = 0;
// 将第一个数组的元素添加到并集数组
for (int i = 0; i < size1; i++) {
if (!isInArray(arr1[i], unionArr, unionSize)) {
unionArr[unionSize++] = arr1[i];
}
}
// 将第二个数组中不在并集数组的元素添加到并集数组
for (int i = 0; i < size2; i++) {
if (!isInArray(arr2[i], unionArr, unionSize)) {
unionArr[unionSize++] = arr2[i];
}
}
- 6.查找矩阵中特殊值
// 找出矩阵的鞍点,即该位置上的元素在该行上最大、在该列上最小。注意:矩阵可能没有鞍点,最多有1个鞍点。如数组{{1, 2, 7, 6}, {2, 6, 10, 3}, {9, 8, 12, 4}, {7, 5, 20, 3}}的鞍点为第 1 行第 3 列的 7
int i, j, k, r, a[M][N], max, max_j, flag; // max_j 为某行最大值所在的列索引
for (i = 0; i < M; i++) { // 遍历 M 行
max = a[i][0]; // 假设各行第 1 个数是本行最大数
// 第 1 个内循环
for (j = 1; j < N; j++) { // 从每行第 2 个数开始遍历
if (a[i][j] > max) {
max = a[i][j]; // 更新最大值, 若多个最大值, max 是列标最小的那一个
max_j = j;
}
} // 内循环结束
// 每一行的最大值可能有2个或多个
// 以数组{{1, 2, 7, 7, 6}, {3, 5, 8, 10, 3}, {2, 4, 3, 8, 2}, {6, 9, 1, 9, 3}}为例, 第 1 行两个 7 均为最大值, 第 1 个 7 所在位置不是鞍点, 第 2 个 7 所在位置为鞍点。因此不建议直接
// 基于 max 所在的列 max_j 进行遍历,这样会忽略掉上述数组中的第 2 个 7, 得出没有鞍点的错误结论
// 为此从第 i 行第 max_j 列位置开始遍历,依次找到与 max 相同的值,然后遍历该值所在列找最小值
// 第 2 个内循环
for (r = max_j; r < N; r++) { // 从第 i 行最大值所在列向后遍历
if(a[i][r] == max) {
max_j = r; // 更新 max_j
flag = 1; // 假设 (i, max_j) 为鞍点
for (k = 0; k < M; k++) { // 遍历 max_j 所在的列
if (max > a[k][max_j]) { // 该列存在比 max 还小的数
flag = 0; // (i, max_j) 位置的元素不是鞍点
break; // 行标 k 之后的行都没必要再遍历,直接退出 for 循环
}
}
// max_j 所在列遍历结束后 flag 值未变,则鞍点存在
if (flag) {
printf("a[%d][%d]=%d\n", i, max_j, max);
return 0;
}
}
}
}
// M行全部遍历结束后flag仍为0,则不存在鞍点
if (!flag) {
printf("It is not exist!\n");
}
// 以下代码未考虑到每行最大值可能有多个的情况,可能会出现错误判断
int i, j, k, a[N][M], max, max_j, flag;
for (i = 0; i < N; i++) {
max = a[i][0];
max_j = 0;
for (j = 1; j < M; j++) {
if (a[i][j] > max) {
max = a[i][j];
max_j = j;
}
}
flag = 1;
for (k = 0; k < N; k++) {
if (max > a[k][max_j]) {
flag = 0;
break;
}
}
if (flag) {
printf("a[%d][%d]=%d\n", i, maxj, max);
break;
}
}
if (!flag) {
printf("It is not exist!\n");
}
- 7.矩阵的运算
// 7.1 矩阵求和
for(i = 0; i < ROWS; i++) {
for(j = 0; j < COLS; j++) {
t[i][j] = s[i][j] + r[i][j];
}
}
// 7.2 矩阵求积
// 设矩阵 A 是 m 行 p 列,矩阵 B 为 p 行 n 列,那么矩阵 A 与 B 的乘积 C = AB 是一个 m 行 n 列矩阵,其运算规则如下:
// 1.确定 C 的维度:矩阵 A 的列数必须等于矩阵 B 的行数,才能进行矩阵乘法运算;乘积矩阵 C 的行数等于矩阵 A 的行数,列数等于矩阵 B 的列数。
// 2.计算乘积矩阵的元素:C 中第 i 行第 j 列的元素 c[i][j] 等于矩阵 A 的第 i 行与矩阵 B 的第 j 列对应元素乘积之和
for (i = 0; i < M; i++) {
for (j = 0; j < N; j++) {
c[i][j] = 0;
for (k = 0; k < N; k++) {
c[i][j] += a[i][k] * b[k][j];
}
}
}
- 8.一些规律
// 数组前 n 个数的下标范围:0 ~ n-1,后 n 个数的下标范围:N-n ~ N-1,N 为数组元素个数
// 身份证号下标 6-13 为出生年月日部分,下标 6-9 为年,10、11为月,12、13为日
// 字符数组的长度通常大于字符串长度,字符串的 '\0' 位置必须具备,否则可能输出乱码
// 字符数组可根据情况直接初始化为 {'\0'}
// 长度为 length 的字符串,当 length 为奇数时 C 位下标为 length/2,否则中间两字符下标分别为length/2 - 1和 length/2
考点5:图形打印
// 这类题目的本质与打印"九九乘法表"类似,宏观上(外循环)看一共有多少行,微观上(内循环)看每一行的内容,若每行有多种字符,可能需要 2 个或更多并列的内循环
// 打印平行四边形
for (i = 1; i < 6; i++) {
// 1.打印每一行开始的空格部分
for (j = 1; j < i; j++) {
printf(" ");
}
// 2.打印每一行空格后的星号部分
for (k = 1; k < 6; k++) {
printf("* ");
}
// 3.行末要换行
printf("\n");
}

// 打印菱形
for (i = 1; i <= ROW; i++) { // 前 ROW 行
// 1.打印每一行开始的空格部分,依次为 ROW-1、ROW-2、...、1、0
for (j = ROW - i; j > 0; j--) {
printf(" ");
}
// 2.打印每一行空格后的星号部分,依次为1、3、5、...、2*ROW-1
for (k = i * 2 - 1; k > 0 ; k--) {
printf("*");
}
// 3.行末要换行
printf("\n");
}
for (i = 1; i <= ROW - 1; i++) { // 后 ROW-1 行
// 1.打印每一行开始的空格部分,依次为 1、2、3、...、ROW-1
for (j = i; j > 0; j--) {
printf(" ");
}
num = ROW * 2 - 1;
for (k = num - 2 * i; k > 0 ; k--) {
printf("*");
}
printf("\n");
}
// 每一行前方的空格数和后面紧挨的"*"数与行号有一定的数量关系,而且外循环的i从0还是1开始也会影响代码量,写代码时要注意

考点6:进制转换
// 十进制转八进制、二进制、十六进制用短除法,八进制、二进制、十六进制转十进制用按权相乘再相加。详细的计算方法参考进制专题
// 1.输入一个合法的八进制正整数,转为十进制并输出。将八进制数的最低位依次拆分出来,与位权相乘
int num, a, t = 1, sum = 0;
while(num){ // 该算法即多位数拆分的变形
a = num % 10; // 拆出八进制正整数的最低位
sum = sum + a * t;
num /= 10; // 丢弃最后一位数
t *= 8; // 位权提升,从最开始的1到8、16、...
}
printf("sum=%d", sum);
int t = 1;
while(num){
a = num % 10;
sum = sum + a * pow(8, t); // 通过数学函数的方式累加
num /= 10;
t++; // 指数提升
}
printf("sum=%d", sum);
// 2.输入一个合法的十六进制数,转为十进制并输出。计算前可先将大写字母(如果有)统一转为小写字母
length = (int)strlen(s), a = 1;
for (i = length - 1; i >= 0; i--) { // 遍历字符串的每一个字符
t = s[i];
if (t >= '0'&&t <= '9') {
b = t - '0'; // 将数字字符转为对应数字
}
else {
if(t >= 'A' && t <= 'Z') {
t = t + 32;
}
b = t - 87; // 将英文字符转为10-15
}
sum = sum + b * a;
a *= 16;
}
printf("十进制值为:%d\n", sum);
// 3.输入一个十进制数,输出对应的二进制
// 方法1:非递归
int n, i = 0, j, bin[MAX]; // 数组bin存储最终的二进制01代码
while (n) { // 该算法也是拆分多位数的变形,完成了模除 2 取余数
bin[i++] = n % 2;
n /= 2;
}
for (j = i - 1; j >= 0; j--) { // 余数倒序相连
printf("%d", bin[j]);
}
// 方法2:递归
// 余数倒序相连的过程恰好跟递归终止条件触发后各级函数调用返回的过程一致
void convert(int m) {
if (m == 1) {
printf("%d", m);
}
else {
convert(m / 2);
printf("%d", m % 2);
}
}
考点7:排序算法
- 1.冒泡排序
// 最最基础的排序算法,必须掌握,算法介绍见排序专题,下同
int bubble_sort(int s[], int n){ // flag 语句可以删掉
int i, j, temp, flag;
for (i = 0; i < n - 1; i++) {
flag = 0; // 假设已经排好序了
for (j = 0; j < n - i - 1; j++) {
if(s[j] > s[j+1]){
temp = s[j];
s[j] = s[j + 1];
s[j + 1] = temp;
flag = 1; // 只要有交换,就重新置1,表示还没排好
}
}
if(!flag){ // 经过一轮后,若 flag 依然未变,则已经有序,直接结束
return 0;
}
}
return 0;
}
- 2.选择排序
void select_sort(int s[], int n){
int i, j, temp, min_loc;
for(i = 0;i < n - 1; i++){
min_loc = i;
for(j = i + 1; j < n; j++){
if(s[j] < s[min_loc]){
min_loc = j;
}
}
if(min_loc != i){
temp = s[min_loc];
s[min_loc] = s[i];
s[i] = temp;
}
}
}
// 有的题目通过排序去做具有一定可行性,如打印数组中与平均值差的绝对值最小的数、前k大的数、前k小的数等
- 3.插入排序
// 与字符数组插入字符后保持有序的算法基本一致,必须熟练掌握
void insert_sort(int s[], int n) {
int i, j, temp;
for (i = 1; i < n; i++) { // 单个数默认有序,因此 i 从下标 1 开始
j = i - 1; // 遍历 i 之前的所有数,这些事都已经有序
temp = s[i]; // 暂存,避免 i 之前的数后移覆盖了 s[i]
while (j >= 0 && s[j] > temp) {
s[j + 1] = s[j]; // 后移
j--;
}
s[j + 1] = temp;
}
}
- 4.计数排序的思想应用

// 前提:待排序数组的元素值均为非负数,也可以是字符;需要两个数组
// 将原数组的元素值映射为计数数组的索引,原数组元素出现次数映射为计数数组的值
// 应用1:输出正整数数组或字符数组中出现次数最多的元素并显示其次数
// 应用2:删除字符数组中的重复字符,每个字符只出现一次。ch1 存原字符串,ch2 存结果字符串
// cnt 数组中的下标为原字符串中字符的 ASCII 码值,下标对应值为 0(字符刚刚出现) 或 1(字符已经出现)
char ch1[MAX], ch2[MAX], c;
int i, j = 0, index, cnt[256] = {0};
for (i = 0; ch1[i] != '\0'; i++) {
c = ch1[i];
index = (int)c; // 字符强转为整型作为下标
if (cnt[index] == 0) { // 表示该字符刚出现
cnt[index]++; // 对应值由 0 置 为 1
ch2[j++] = c; // 将这个刚出现的字符存入 ch2
}
}
ch2[j] = '\0';
// 计数排序的思想在上述应用中能够巧妙地写出时间复杂度为O(n)的程序
考点8:字符数组基础
// 1.常用字符的ASCII码
空字符--->0 空格符--->32 '0'--->48 '9'--->57 'a'--->97 'z'--->122 'A'--->65 'Z'--->90
// 2.头文件及常用函数
string.h---> strlen() strcpy() strncpy() strcat() strncat() strcmp() strncmp() 带n的了解为主
ctype.h---> isalpha() islower() isupper() isdigit()
// 2.1 编写代码实现函数 strlen() 的功能
int my_strlen(char str[]) {
int length = 0;
while (str[length] != '\0') {
length++;
}
return length;
}
// 2.2 编写代码实现函数 strcpy() 的功能
void my_strcpy(char dest[], char src[]) {
int i = 0;
while (src[i] != '\0') {
dest[i] = src[i];
i++;
}
dest[i] = '\0';
}
// 2.3 编写代码实现函数 strcat() 的功能
void my_strcat(char dest[], const char src[]) {
int dest_index = 0;
// 找到目标字符串的结束位置
while (dest[dest_index] != '\0') {
dest_index++;
}
int src_index = 0;
// 将源字符串复制到目标字符串的末尾
while (src[src_index] != '\0') {
dest[dest_index] = src[src_index];
dest_index++;
src_index++;
}
// 添加字符串结束符
dest[dest_index] = '\0';
}
// 字符串拼接案例
int i = 0, j = 0, k = 0, c[k] = {'\0'};
while(a[i] != '\0'){
c[k++] = a[i++];
}
while(b[j] != '\0'){
c[k++] = b[j++];
}
// 2.4 编写代码实现函数 strcmp() 的功能(2种方法),考点9中有基于库函数的字符串大小比较
for (i = 0; s1[i] != '\0' && s2[i] != '\0'; i++) {
if (s1[i] != s2[i]) {
printf("%d\n", s1[i]-s2[i]);
return 0;
}
}
printf("%d\n", s1[i]-s2[i]);
int my_strcmp(const char s1[], const char s2[]) {
int i = 0;
// 比较字符直到遇到其中一个字符串的结束符
while (s1[i] != '\0' && s2[i] != '\0') {
if (s1[i] < s2[i]) {
return -1;
} else if (s1[i] > s2[i]) {
return 1;
}
i++;
}
// 如果 s1 先结束,而 s2 还有字符,s1 小于 s2
if (s1[i] == '\0' && s2[i] != '\0') {
return -1;
}
// 如果 s2 先结束,而 s1 还有字符,s1 大于 s2
else if (s2[i] == '\0' && s1[i] != '\0') {
return 1;
}
// 两个字符串完全相同
return 0;
}
// 2.5 strncpy():复制指定长度的字符串到另一个字符数组
char src[] = "Hello";
char dest[10];
strncpy(dest, src, 3);
dest[3] = '\0';
// 2.6 strncat():将指定长度的字符串追加到另一个字符串末尾
char dest[20] = "Hello";
char src[] = " World";
strncat(dest, src, 3);
// 2.7 strncmp():比较两个字符串的前 n 个字符
char s1[] = "Hello";
char s2[] = "Helly";
int result = strncmp(s1, s2, 3);
if (result == 0) {
printf("First 3 characters are equal.\n");
}
else {
printf("First 3 characters are not equal.\n");
}
// 3.判别英文字符、数字字符、大小写字母转换
// 在不影响题目需求时,字母统一大小写可简化计算,如十六进制数转十进制数
(t >= 'A' && t <= 'Z') || (t >= 'a' && t <= 'z') 简化为 isalpha(t)
t >= '0' && t <= '9' 简化为 isdigit(t)
c = c + 32; 简化为 toupper(c)
c = c - 32; 简化为 tolower(c)
// 4.连续的数字字符转为对应的整型数字,如"1262"转为1262
'5' - '0' = 5 '9' - '0' = 9
t = 0; t = t * 10 + s[i] - '0'
int convert(char s[]) {
int i, result = 0;
for(i = 0; s[i] != '\0'; i++) {
if(s[i] >= '0' && s[i] <= '9') {
result = result * 10 + s[i] - '0';
}
else {
break;
}
}
return result;
}
// 引申:将字符串中出现的连续数字字符作为一个整数,依次存放到数组中。如"ab127xe65dx123",将127 65 123 存入数组
t = 0, k = 0;
for (i = 0; i <= length; i++) { // "="要加上,否则到 '\0' 会直接退出循环,若 '\0' 前方刚好有数,数据没有写到数组中
if (isdigit(s[i])) { // 只要有连续或单独的数字字符出现都会执行该分支
t = t * 10 + s[i] - '0';
}
// 只要当前字符非数字字符但前一个字符是数字字符,意味着上一个单独数字字符或连续数字字符结束,此时将 t 值写入数组并重新置0
else if(i >= 1 && isdigit(s[i-1])){ // 防止 i = 0 时减 1 越界
a[k++] = t;
t = 0;
}
}
考点9:字符数组比较大小
// 1.三个字符串比较大小(熟练使用字符串库函数)
char s1[MAX] = "hello", s2[MAX] = "hEloo", s3[MAX] = "Welcome";
char max[MAX];
if (strcmp(s1, s2) > 0) {
strcpy(max, s1);
}
else{
strcpy(max, s2);
}
if (strcmp(s3, max) > 0 ) {
strcpy(max, s3);
}
// 2.根据两人身份证号输出出生年月,并比较年龄大小
char id[2][19], birth[2][9];
for (i = 0; i < 2; i++) {
k = 0;
for (j = 6; j < 14; j++) {
birth[i][k] = id[i][j];
k++;
}
birth[i][k] = '\0';
}
if (strcmp(birth[0], birth[1]) < 0) { // 熟练使用库函数进行比较
printf("第1个人的年龄更大\n");
}
else if (strcmp(birth[0], birth[1]) > 0) {
printf("第2个人的年龄更大\n");
}
else {
printf("两人的年龄一样大\n");
}
// 3.登录密码验证
char pwd[100] = {0};
int count = 3;
while(count > 0){
printf("请输入密码: \n");
gets(pwd);
if(strcmp(pwd, "wljspass666")==0){
printf("登录成功!\n");
break;
}
else{
count--; // 密码输入错误,可用次数减少
if(count == 0){
printf("次数已用完,账户被锁定!\n");
}
}
}
考点10:字符数组中字符移动相关(以增加、删除字符为例)
// 1.有序字符数组插入新字符后仍保持有序,从下标 length - 1 处开始逐次后移,为待插入字符空出位置
// 注意待插入字符如果在字符串最前方可能会导致下标越界,循环退出时待插入字符的位置是 i + 1
while(i >= 0 && s[i] > c){
s[i + 1] = s[i];
i--;
}
s[i + 1] = c;
s[++length] = '\0';
// 如果题目涉及到字符串中个别字符“跳跃移动”的情况(即不像上题中有规律地逐次后移),要注意“跳跃移动”期间字符数组的长度是否足够,原字符串
// 最后的 '\0' 是否被覆盖,如果没有被覆盖打印输出字符串时不要直接用puts和%s,如果被覆盖,新的 '\0' 位置要定位。跳过的字符位置若没有初值,在输出时可能会有乱码
// 2.将字符串中的大写字符统一往后移动4位。定义字符数组时可直接赋值为 {'\0'}
i = length - 1;
while(i >= 0){
if(s[i] >= 'A'&& s[i] <= 'Z'){
s[i+4] = s[i];
}
i--;
}
s[length + 4] = '\0';
for(i = 0; i < length + 4; i++){
printf("%c", s[i]);
}
// 3.删除字符串最后方连续的"*"
for(i = length - 1; i >= 0; i--){
if(s[i] == '*'){
s[i] = '\0';
}
else {
break;
}
}
puts(s);
// 4.删除字符串中重复的字符,保证每个字符只输出 1 次
// 方法 1 见考点 7,方法 2 为普通方法
for(i = 0; i < length - 1; i++){ // i 的范围最终到倒数第 2 个字符
for(j = i + 1; s[j] != '\0'; j++){ // j 始终指向 i 后方,范围为 i + 1 ~ length - 1
k = j;
// 只要 k 指向的字符和 i 指向的字符一致,那就将 k 后方的所有字符依次往前移动一个单位
if(s[k] == s[i]){
while(s[k] != '\0'){
s[k] = s[k + 1];
k++;
}
length--;
}
// 如果重复字符后方所有字符往前移动后,j 指向的字符依然和 i 相同(即有连续不少于两个相同的字符),如果直接执行内循环中的 j++,这个重复字符就保留了下来
// 所以先执行 j-- 再执行内循环中的 j++,保证 j 的位置没变,继续删除重复字符
if(s[j] == s[i]){
j--;
}
}
}
// 5.删除字符串中所有的空格符
while(s[i] != '\0'){ // i 值为 length - 1,即 '\0' 时循环退出
if(s[i] == ' '){
for(j = i + 1; j <= length; j++){ // 该循环用于将空格字符后的所有字符往前移动, 含索引为 length的 '\0'
s[j - 1] = s[j];
}
length--; // 字符串长度修改
if(s[i] == ' '){ // 如果有 2 个或 2 个以上连续的空格存在, 此时即使第 1 个空格之后的所有字符往前移动了, 但 i 指向的位置依然是空格, 所以在执行 i 自增之前先做一次自减的操作, 以保证后续空格也被消除
i--;
}
}
i++;
}
// 6.在字符串(长度大于3)的第3个字符后方加一个"#"
for(i = length; i >= 3; i--){
s[i + 1] = s[i]; // 从最后的 '\0' 字符到第 4 个字符均后移
}
s[i + 1] = '#';
// 7.将字符串中每两个相邻字符之间插入一个空格,如输入"helloworld",应输出"h e l l o w o r l d"
for (i = length - 1; i >= 0; i--) { // 从后往前遍历字符串
s[i * 2] = s[i]; // 将当前字符移动到当前索引 2 倍的位置
s[i * 2 + 1] = ' '; // 后方再加个' '
}
length = length * 2 - 1;
s[length] = '\0';
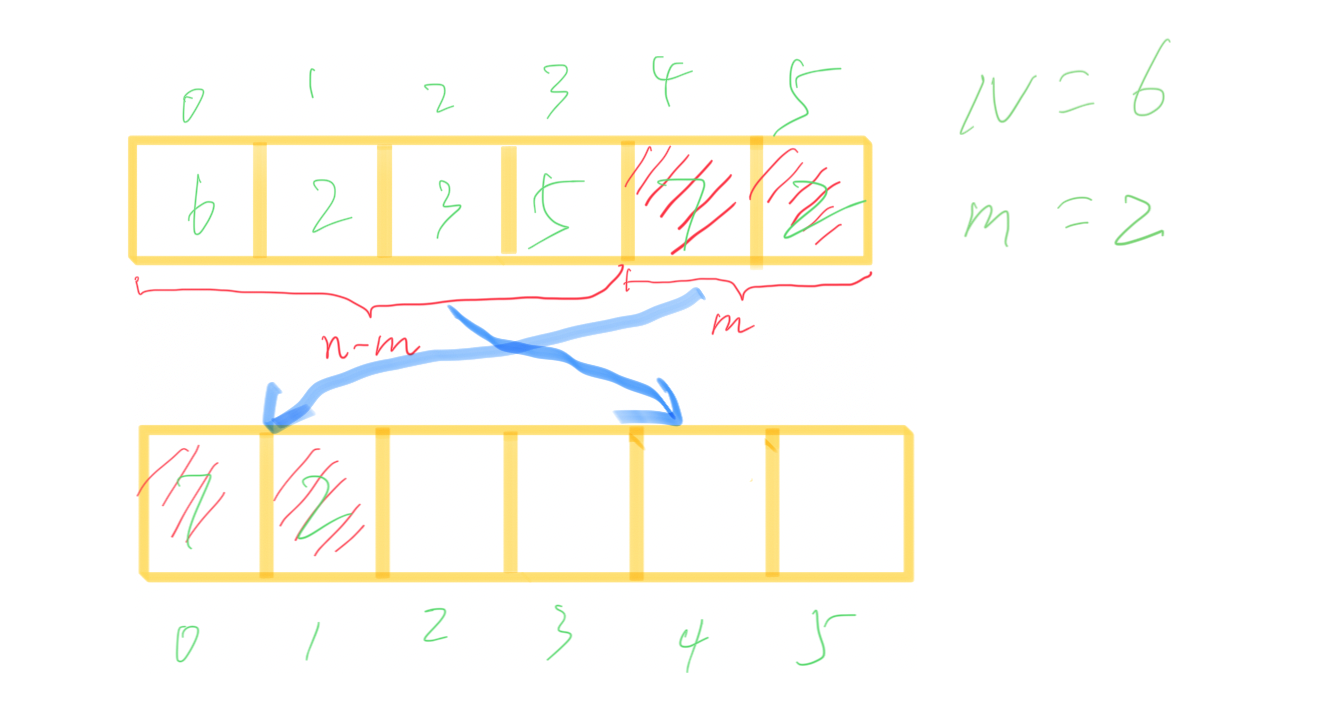
// 8.有 n 个整数,使前面各数顺序向后移动 m 个位置(m < n),输出调整后的 n 个数
int a[N] = {4, 6, 1, 5, 0, 7, 2, 3}, temp[N];
int m, i, j = 0;
if (m == 0||m == N) {
printf("无需移动!");
}
else if (m < 0) {
printf("数值异常, end...");
return -1;
}
else {
for (i = N - m; i < N; i++) { // 将后 m 个数按顺序暂存到 temp 中
temp[j++] = a[i];
}
for (i = N - m - 1; i >= 0; i--) { // 将前 n - m 个数往后移
a[i + m] = a[i];
}
for (i = 0; i < m; i++) { // 再将 temp 中暂存的数复位到空出的前 m 个位置
a[i] = temp[i];
}
}
考点11:字符数组特征探索
// 1.回文数组(2种方法)
char s[MAX], i = 0, j = strlen(s) - 1;
while(i < j){ // 此处没必要加"=",奇数位字符中间位不用自身比较,偶数位字符中间两位不会出现 i == j 的情况
if(s[i] != s[j]) {
printf("No!\n");
return -1;
}
i++;
j--;
}
printf("Yes!");
// 关于索引为 length / 2 的位置,长度为奇数时恰好是C位下标,长度为偶数时下标为中间两字符右边的那一位
int isPalindrome(char arr[], int length) {
for (int i = 0; i < length / 2; i++) {
if (arr[i] != arr[length - 1 - i]) {
return 0;
}
}
return 1;
}
// 回文数
t = num;
while(t){
a[j] = t % 10;
j++;
t /= 10;
}
for(k = 0; k < j / 2; k++){ // k 为对称比较数据的下标
if(a[k] != a[j - k - 1]){
break;
}
}
if(k == j / 2){ // for循环正常退出时执行
printf("%d是回文数\n", num);
}
// 2.合法用户名或密码:必须同时存在字母、数字和其他字符,缺一不可
int is_valid_username(char username[], int length) {
int has_letter = 0;
int has_digit = 0;
int has_other = 0;
for (int i = 0; i < length; i++) {
if (isalpha(username[i])) {
has_letter = 1;
} else if (isdigit(username[i])) {
has_digit = 1;
} else {
has_other = 1;
}
}
return has_letter && has_digit && has_other;
}
// 3.字符元素的循环替换(以凯撒密码、密码破译为例)
// 3.1 将字母A变成字母E,a变成e,即变成其后的第4个字母,W变成A,X变成B,Y变成C,Z变成D,输入字符串加密为对应的密码(2种方法)
while (ch != '\n') {
if((ch >= 'W'&&ch <= 'Z')||(ch >= 'w'&&ch <= 'z')){
ch -= 22;
}
else if ((ch >= 'A'&&ch <= 'V')||(ch >= 'a'&&ch <= 'v')){
ch +=4;
}
putchar(ch);
ch = getchar();
}
while (ch != '\n') {
if((ch >= 'A'&&ch <= 'Z')||(ch >= 'a'&&ch <= 'z')){
ch += 4;
if(ch >= 'Z' + 1 && ch <= 'Z' + 4 || ch >= 'z' + 1&& ch <= 'z' + 4) {
ch -= 26;
}
}
putchar(ch);
ch = getchar();
}
// 3.2 有一行电文已按以下规律加密为密码:A—>Z a—>z B—>Y b—>y C—>X c—>x…即第1个字母变为第26个字母,第2个字母变为第25个字母…第i个字母变成第26-i+1个字母,非字母字符不变。编程将密码译回原文,并输出密码和原文。如输入密文"R droo erhrg Xsrmz mvcg dvvp." 输出"I will visit China next week."
code[] = {' ', 'a', 'b', 'c', ..., 'z'};
for (i = 0; pwd[i] != '\0'; i++) {
t = pwd[i];
if (isupper(t)) {
putchar(code[26 - t + 'A'] - 32); // 大写字母 t 在26个字母中的序号为 t - 'A' + 1,由此可知对应的密文位置为 26 - (t - 'A' + 1) + 1 = 26 - t + 'A',作为下标,t 的值为code[26 - t + 'A'] - 32
}
else if (islower(t)) {
putchar(code[26 - t + 'a']);
}
else {
putchar(t);
}
}
// 3.3 将字符串中的数字字符加6,字符'4'加6后的结果按字符'0'计算,字符'5'加6后的结果按字符'1'计算
while (s[i] != '\0') {
t = s[i];
if (t >= '0'&&t <= '3') {
s[i] += 6;
}
else if (t >= '4'&& t <= '9') {
s[i] -= 4;
}
i++;
}
// 3.4 判断是字母字符串、数字字符串还是其他字符串
int i = 0, alpha_flag = 0, num_flag = 0;
while(s[i] != '\0'){
t = s[i];
if(alpha_flag == 0 && ((t >= 'A' && t <= 'Z') || (t >= 'a' && t <= 'z'))) {
alpha_flag = 1;
}
else if(num_flag == 0 && (t >= '0' && t <= '9')) {
num_flag = 1;
}
i++;
}
if(alpha_flag==1&&num_flag==0){
printf("是字母字符串");
}
else if(alpha_flag==0&&num_flag==1){
printf("是数字符串");
}
else{
printf("是其他符串");
}
考点12:字符数组中的英文单词(标志变量)
// 1.统计字符串中的单词个数,单词之间用空格分开
int i = 0, word = 0, count = 0; // word 是新单词开始的标记
while(s[i] != '\0'){
if(s[i] != ' ' && word == 0){ // 新单词开始
word = 1;
count++;
}
if(s[i] == ' '){ // 此处不能写 else 语句,因为 else 还含有word为 1 的情况,此时可能并未出现新单词
word = 0;
}
i++;
}
// 2.输出字符串中最长的单词,单词之间用空格分开
// 方法1:将s中的第1个单词存入数组words并记录其长度,后续出现更长的单词就替换前一个单词并记录新的长度,直到s遍历结束
char s[MAX], words[MAX] = {'\0'}; // words存完新单词后无需专门再赋值'\0'
// i: 遍历s时的索引 j: 将s中的单词存储到words中时s的索引
// k: words的索引 word: 单词开始标志变量 max_length:最长单词的长度
int word = 0, max_length = 0;
for (i = 0; s[i] != '\0'; i++) {
if (s[i] != ' ' && word == 0) { // 新单词开始标志
word = 1;
for (j = i; s[j] != ' ' && s[j] != '\0'; j++); // 遍历到新单词的结尾
if (j - i > max_length) { // 计算新单词长度与最大单词长度比较
max_length = j - i;
for (k = 0, j = i; j < i + max_length; j++) { // 将新单词覆盖到words中
words[k++] = s[j];
}
}
}
if (s[i] == ' ') { // 当前单词结束
word = 0;
}
}
puts(words); // 打印最长的单词
// 方法2:以空格作为间隔,将字符串s中各单词存储到二维数组split_s中,打印split_s中最长的字符串
char s[MAX], split_s[MAX/2][MAX] = {'\0'}; // split_s每一行后无需专门再赋值'\0'
// i: 遍历s时的索引 j: 将s中的单词存储到split_s中时的索引 m: split_s的行索引
// n: split_s的列索引 word: 单词开始标志变量 max_index: 最长单词的索引
int m = 0, n, word = 0, max_index;
for (i = 0; s[i] != '\0'; i++) {
if (s[i] != ' ' && word == 0) { // 新单词开始标志
word = 1;
n = 0;
for (j = i; s[j] != ' ' && s[j] != '\0'; j++) {
split_s[m][n++] = s[j];
}
m++;
}
if (s[i] == ' ') { // 单词结束
word = 0;
}
}
max_index = 0;
for (i = 1; i < m; i++) {
if (strlen(split_s[i]) > strlen(split_s[max_index])) {
max_index = i;
}
}
puts(split_s[max_index]);
考点13:模拟点餐程序
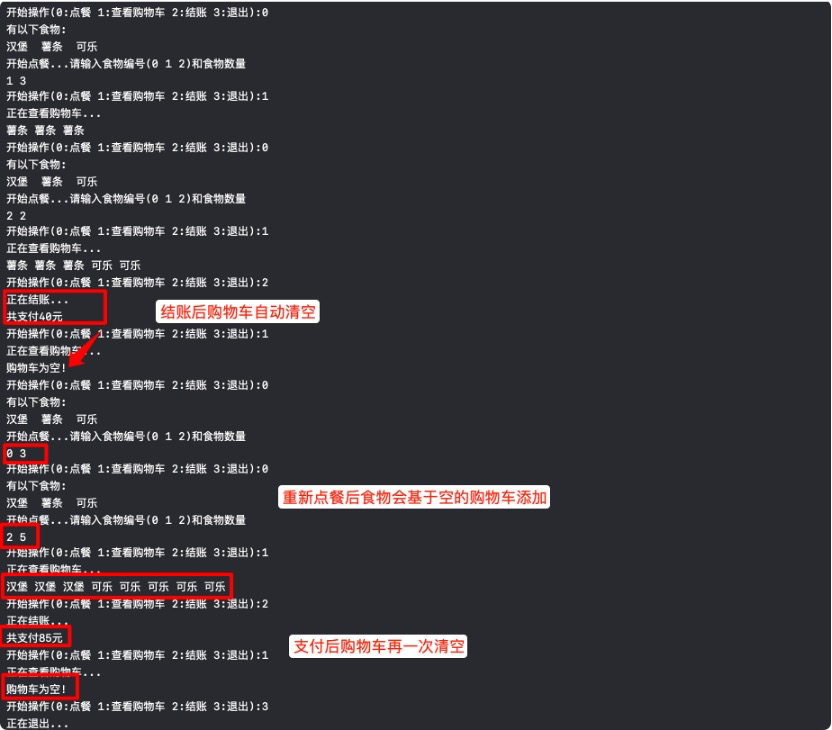
// 定义数组food和price,定义整型变量c、n和op,其中c为食物编号,n为编号c对应的食物数量,op为功能选项(0:点餐, 1:查看购物车,2:结账,3:退出点餐程序,
// 其他值:提示错误并要求重新输入)。现要求用户输入c、n和op值,打印输出相应的结果。运行结果如下:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define ITEM 3 // 食物种类
#define LEN 1000 // 每种食物占据的最长字节数
#define MAX 1000 // 购物车可加食物数量上限
int car_length = 0; // 购物车数组的长度,全局变量
void print_food(char food[][LEN]) {
int i;
for (i = 0; i < ITEM; i++) {
printf("%s ", food[i]);
}
}
void add_food(char food[][LEN], char car[][LEN], int c, int n) { // c:食物编号 n:食物数量
int i;
for (i = car_length; i < car_length + n; i++) {
strcpy(car[i] ,food[c]);
}
car_length = i; // 更新长度,后续可能会继续在购物车中增加物品,所以当前的长度需要保存
}
void print_car(char car[][LEN]){
int i = 0;
while (car[i][0] != '\0') { // 购物车数组中某行的字符串中0列为'\0',代表此处为空的,未存储食物
printf("%s ", car[i]);
i++;
}
if (i == 0) {
printf("购物车为空!");
}
printf("\n");
}
int cal_pay(char car[][LEN], int price[]) {
int pay = 0, i;
for (i = 0; car[i][0] != '\0'; i++) { // 遍历购物车结束条件也是某行0列字符为'\0'
if (strcmp(car[i], "汉堡") == 0) {
pay += price[0];
}
else if (strcmp(car[i], "薯条") == 0) {
pay += price[1];
}
else {
pay += price[2];
}
strcpy(car[i], "\0"); // i位置处的食物算入总价后,就将i位置处的内容置为"\0",支付的过程即伴随着清空购物车.此处清空购物车只是数组中每行为"\0",但购物车长度不是0
}
car_length = 0; // 所以此处也要将购物车的长度置零,在下方case 2处置零也可以
return pay;
}
int main(int argc, const char * argv[]) {
// insert code here...
char food[ITEM][LEN] = {"汉堡", "薯条", "可乐"};
int c, n, op, money, price[ITEM] = {20, 10, 5}; // c:食物编号 n:食物数量 op:功能选项
char car[MAX][LEN] = {'\0'}; // 购物车,直接初始化为'\0',利于后续处理中找到car数组的边界
while (1) {
printf("开始操作(0:点餐 1:查看购物车 2:结账 3:退出):");
scanf("%d", &op);
switch (op) {
case 0:
printf("有以下食物:\n");
print_food(food);
printf("\n开始点餐...请输入食物编号(0 1 2)和食物数量\n");
scanf("%d %d", &c, &n);
add_food(food, car, c, n);
break;
case 1:
printf("正在查看购物车...\n");
print_car(car);
break;
case 2:
printf("正在结账...\n");
money = cal_pay(car, price);
printf("共支付%d元\n", money);
// car_length = 0;
break;
case 3:
printf("正在退出...\n");
exit(-1);
default:
printf("功能选项输入错误,请重新输入!\n");
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号