排序专题
简单分析以下排序方法的算法,并分别用Python代码和C代码实现升序排列
- 0.先写一个装饰器,用于计算排序算法的执行时间
import time
def wrapper(func):
def inner(*args, **kwargs):
start_time = time.time()
v = func(*args, **kwargs)
end_time = time.time()
print("%s running time: %s secs." %(func.__name__, end_time - start_time))
return v
return inner
-
1.冒泡排序
- 算法思想
- 1.从第1个元素开始,逐次比较序列中相邻的两个数,如果前面的数更大,则交换彼此。当一趟排序完成后,无序区减少一个数,有序区增加一个数,即处于尾部的最大数
- 2.重复上述步骤共N-1趟(N为序列中元素总个数),可得到排好的序列
- Python代码
import random from cal_time import wrapper @wrapper def bubble_sort(li): for i in range(len(li) - 1): # 第i趟 exchange = False # 标志变量exchange for j in range(len(li) - i - 1): if li[j] > li[j + 1]: li[j], li[j+1] = li[j+1], li[j] exchange = True # 如果在某趟中没有发生交换,则代表序列已有序 if not exchange: return li = list(range(10000)) random.shuffle(li) bubble_sort(li)![]()
- C语言代码
#include <stdio.h> int bubble_sort(int s[], int n){ int i, j, temp, flag; for(i = 0;i < n - 1; i++){ flag = 0; for(j = 0;j < n - i - 1; j++){ if(s[j] > s[j+1]){ temp = s[j]; s[j] = s[j+1]; s[j+1] = temp; flag = 1; } } if(!flag){ return 0; } } return 0; } void print_arr(int s[], int n){ int i; for(i = 0; i < n; i++){ printf("%d ", s[i]); } } int main(){ int a[5], i; printf("请输入5个序列元素:\n"); for(i = 0;i < 5;i++){ scanf("%d", &a[i]); } printf("排序前的序列为:"); print_arr(a, 5); bubble_sort(a, 5); printf("\n排序后的序列为:"); print_arr(a, 5); return 0; }![]()
- 过程模拟
![]()
- 算法思想
-
2.选择排序
- 算法思想
- 1.假设无序区的第1个数A1为最小数,遍历该数后方序列的所有数找到最小数B1(假设B1存在),将A1与B1交换,此时完成了第1趟排序。序列的第1个数为最小数(有序区),后方N-1个数为无序区
- 注意:通过保留数的下标来完成交换
- 2.假设无序区的第1个数A2为最小数(A2即整个序列的第2个数),遍历此数后方序列的所有数找到最小数B2(假设B2存在),将A2与B2交换,此时完成了第2趟排序。序列的前2个数为最小数与次小数(有序区),后方N-2个数为无序区
- 3.继续重复上述操作,直到完成第N-1趟排序,可得到排好的序列
- 1.假设无序区的第1个数A1为最小数,遍历该数后方序列的所有数找到最小数B1(假设B1存在),将A1与B1交换,此时完成了第1趟排序。序列的第1个数为最小数(有序区),后方N-1个数为无序区
- Python代码
import random from cal_time import wrapper @warpper def select_sort(li): for i in range(len(li) - 1): # i是第几趟 min_loc = i # 记录无序区的第1个位置 for j in range(i + 1, len(li)): if li[j] < li[min_loc]: min_loc = j if min_loc != i: # 找到了更小的数。该行可省 li[i], li[min_loc] = li[min_loc], li[i] # 将无序区最小的数与本轮第1个数交换 li = list(range(10000)) random.shuffle(li) print(li) select_sort(li) print(li)![]()
- C语言代码
#include <stdio.h> void select_sort(int s[], int n){ int i, j, temp, min_loc; for(i = 0;i < n - 1; i++){ min_loc = i; for(j = i + 1; j < n; j++){ if(s[j] < s[min_loc]){ min_loc = j; } } if(min_loc != i){ temp = s[min_loc]; s[min_loc] = s[i]; s[i] = temp; } } } void print_arr(int s[], int n){ int i; for(i = 0; i < n; i++){ printf("%d ", s[i]); } } int main(){ int a[7], i; printf("请输入7个序列元素:\n"); for(i = 0; i < 7; i++){ scanf("%d", &a[i]); } printf("排序前的序列为:"); print_arr(a, 7); select_sort(a, 7); printf("\n排序后的序列为:"); print_arr(a, 7); return 0; }![]()
- 过程模拟
![]()
![]()
- 算法思想
-
3.插入排序
- 算法思想
- 0.运行过程与打牌非常相似,第1张牌拿到后,后续牌的位置基于现有排好序的牌插入
- 1.假设序列中的第1个数为有序区,后方N-1个数为无序区。用第2个数和有序区(第1个数)比较,找到合适的位置插入,此时完成了第1趟排序
- 2.序列中的前2个数为有序区,后方N-2个数为无序区。用第3个数和有序区(前2个数)比较,找到合适的位置插入,此时完成了第2趟排序
- 3.继续重复上述操作,直到完成第N-1趟排序,可得到排好的序列
- 注意:插入新数到有序区时,有序区可能会后移,此时会覆盖待插入的数,因此待插入数据要暂存;后移的算法和课本上案例5-12的算法一致,也算是课本案例的应用与扩充
- Python代码
import random from cal_time import wrapper def insert_sort(li): for i in range(1, len(li)): # i表示待插入数据的下标 tmp = li[i] # 暂存待插入数据,防止有序区数据后移而覆盖 j = i - 1 # j表示有序区最后一个数的下标 while j >= 0 and li[j] > tmp: # 情形1:在有序区之间找到了插入位置 情形2:有序区的数都比待插入数据大,j会减到-1导致越界 li[j + 1] = li[j] # 有序区数据从后往前依次后移 j -= 1 li[j + 1] = tmp # 将待插入数据存入 li = list(range(10000)) random.shuffle(li) print(li) insert_sort(li) print(li)![]()
- C语言代码
#include <stdio.h> void insert_sort(int s[], int n){ int i, j, temp; for(i = 1; i < n; i++){ j = i - 1; temp = s[i]; while(j >= 0 && s[j] > temp){ s[j + 1] = s[j]; j --; } s[j + 1] = temp; } } void print_arr(int s[], int n){ int i; for(i = 0; i < n; i++){ printf("%d ", s[i]); } } int main(){ int a[7], i; printf("请输入7个序列元素:\n"); for(i = 0; i < 7; i++){ scanf("%d", &a[i]); } printf("排序前的序列为:"); print_arr(a, 7); insert_sort(a, 7); printf("\n排序后的序列为:"); print_arr(a, 7); return 0; }![]()
- 过程模拟
![]()
- 算法思想
-
4.快速排序
- 算法思想
- 0.选择序列中某个元素作为“基准数”,将所有小于基准数的数移到其左侧,将所有大于基准数的数移到其右侧
- 设定索引i指向序列中第1个元素,索引j指向序列中最后一个(第N个)元素,第1个元素同时作为“基准数”并暂存到temp中
- j往左移动的过程中找到比“基准数”小的数后,将该数移动到i的位置;i往右移动的过程中找到比“基准数”大的数后,将该数移动到j空出来的位置。直到i与j相遇,结束循环,此时“基准数”的位置刚好是分界线,返回“基准数”的下标mid
- 1.递归左子序列(left ~ mid - 1 )和右子序列(mid + 1 ~ right)
- 0.选择序列中某个元素作为“基准数”,将所有小于基准数的数移到其左侧,将所有大于基准数的数移到其右侧
- Python代码
import random from cal_time import wrapper @wrapper def partition(li, left, right): tmp = li[left] # 将left指向的数作为“基准数”暂存 while left < right: while left < right and li[right] >= tmp: # 从右边找比tmp小的数 right -= 1 li[left] = li[right] # 将找到的数写到左边left所在空位上,空位上原数已暂存 while left < right and li[left] <= tmp: # 从左边找比tmp大的数 left += 1 li[right] = li[left] # 将找到的数写到右边right的空位上 li[left] = tmp # 将tmp归位 return left def _quick_sort(li, left, right): if left < right: # 待排序序列中至少有2个元素 mid = partition(li, left, right) # 返回“基准数”的索引 _quick_sort(li, left, mid - 1) # 以基准数为中轴线左右两边递归 _quick_sort(li, mid + 1, right) @wrapper def quick_sort(li): _quick_sort(li, 0, len(li) - 1) li = list(range(10000)) random.shuffle(li) quick_sort(li) print(li)![]()
- C语言代码
#include <stdio.h> int partition(int a[], int left, int right){ int temp = a[left]; while(left < right){ while(left < right && a[right] >= temp){ right --; } a[left] = a[right]; while(left < right && a[left] <= temp){ left ++; } a[right] = a[left]; } a[left] = temp; return left; } void quick_sort(int a[], int left, int right){ int mid; if(left < right){ mid = partition(a, left, right); quick_sort(a, left, mid - 1); quick_sort(a, mid + 1, right); } } void print_arr(int a[], int n){ int i; for(i = 0; i < n; i++){ printf("%d ", a[i]); } } int main(){ int s[7], i; printf("请输入7个序列元素:\n"); for(i = 0; i < 7; i++){ scanf("%d", &s[i]); } printf("排序前的序列为:"); print_arr(s, 7); quick_sort(s, 0, 6); printf("\n排序后的序列为:"); print_arr(s, 7); return 0; }![]()
- 过程模拟
- 注意:图中不同颜色的框可看成不同层次的递归在内存中的分布
![]()
- 注意:图中不同颜色的框可看成不同层次的递归在内存中的分布
- 算法思想
-
5.堆排序
- 铺垫知识
- 1.树是一种可以递归定义的数据结构,是由n个节点组成的集合。如果n=0,则这是一个空树;如果n>0,那存在1个节点作为树的根节点,其他节点可以分为m个集合,每个集合本身又是一棵树
- 2.节点与深度
- 根节点:位于第0层的节点,也称树根
- 叶子结点:没有子节点的节点
- 孩子节点与父节点:若A结点是B结点的父结点,则称B结点是A结点的子结点,也称孩子结点
- 子树:从一棵树中抽取出来的一棵新树,包含了一个原始树中某个节点及其所有的子节点。子树可以是原始树的任意一部分,包括单个节点、整个树,或者是位于树的某个分支上的一部分
- 节点的度:当前节点的向下分叉数(孩子数)
- 树的深度(高度):树的层数
- 树的度:所有节点的度中最大的一个
- 3.二叉树:度不超过2的数,每个节点最多有2个孩子节点,被区分为左孩子节点和右孩子节点
- 4.满二叉树:每一层的节点数都达到最大值的二叉树
- 5.完全二叉树
- 叶节点只能出现在最下层和次下层,并且最下层的节点都集中在该层最左边的若干位置的二叉树
- 如果用列表(顺序存储方式)来存储完全二叉树,若父节点的索引为i,则左孩子节点索引为
2 * i + 1,右孩子节点索引为2 * i + 2;若孩子节点索引为i,则父亲节点索引为(i - 1) // 2
- 6.堆及其调整
- 堆是一种特殊的完全二叉树结构,大根堆满足任意节点都比其孩子节点大,小根堆满足任意节点都比其孩子节点小
- 堆的向下调整:假设节点的左右子树都是堆,但自身不是堆。当根节点的左右子树都是堆时,可以通过一次向下的调整来将其变换成一个堆
- 算法思想
- 0.堆是逻辑上的概念,物理上采用列表或数组来实现
- 1.构造堆,从最后一个有孩子节点的非叶子结点开始,由下往上遍历调整所有相关节点,否则会导致二叉树结构被破坏
- 2.取得堆顶元素,为最大(最小)元素
- 3.去掉堆顶,将堆中最后一个元素放到堆顶,此时可通过一次调整重新使堆有序
- 4.此时堆顶为第2大的元素,重复步骤2-3,直到堆变空
- Python代码
import random def sift(li, low, high): """ :param li: 列表 :param low: 堆的根节点位置,不一定是索引为0的节点,也可能是子树的根节点 :param high: 堆的最后1个元素的位置 """ i = low # i最开始指向根节点 j = 2 * i + 1 # j最开始是i的左孩子 tmp = li[low] # 暂存堆顶元素 while j <= high: # 只要j所在的位置有数 if j + 1 <= high and li[j + 1] > li[j]: # 如果右孩子存在并且比较大 j = j + 1 # j指向右孩子 if li[j] > tmp: li[i] = li[j] i = j # 往下看一层 j = 2 * i + 1 # j继续指向下一个孩子节点 else: # tmp更大,把tmp放到i的位置 li[i] = tmp # 把tmp放到某一级领导的位置 break else: li[i] = tmp # 把tmp放到叶子结点上 @wrapper def heap_sort(li): n = len(li) # 从最后一个叶节点的父节点开始建堆,索引为n - 1节点的父节点,下标为(n - 1 - 1) // 2 for i in range((n - 2) // 2, -1, -1): # i表示建堆的时候调整子树的根的下标 sift(li, i, n - 1) # high指向n - 1,即最后一个位置 # 上述for循环结束后建堆完成了 for i in range(n - 1, -1, -1): # i指向当前堆的最后一个元素 li[0], li[i] = li[i], li[0] # 堆顶和最后一个元素做交换 sift(li, 0, i - 1) # i - 1是新的high li = [i for i in range(10000)] random.shuffle(li) heap_sort(li) print(li)![]()
- C语言代码
#include <stdio.h> void sift(int a[], int low, int high){ int i, j, temp; i = low; j = 2 * i + 1; temp = a[low]; while(j <= high){ if(j + 1 <= high && a[j + 1] > a[j]){ j = j + 1; } if(a[j] > temp){ a[i] = a[j]; i = j; j = 2 * i + 1; } else { break; } } a[i] = temp; } void heap_sort(int a[], int n){ int i, temp; for(i = (n - 2) / 2; i >= 0; i--){ sift(a, i, n - 1); } for(i = n - 1; i >= 0; i--){ temp = a[0]; a[0] = a[i]; a[i] = temp; sift(a, 0, i - 1); } } void print_arr(int a[], int n){ int i; for(i = 0; i < n; i++){ printf("%d ", a[i]); } } int main(){ int s[7], i; printf("请输入7个序列元素:\n"); for(i = 0; i < 7; i++){ scanf("%d", &s[i]); } printf("堆序前的序列为:"); print_arr(s, 7); heap_sort(s, 7); printf("\n堆排序后的序列为:"); print_arr(s, 7); return 0; }![]()
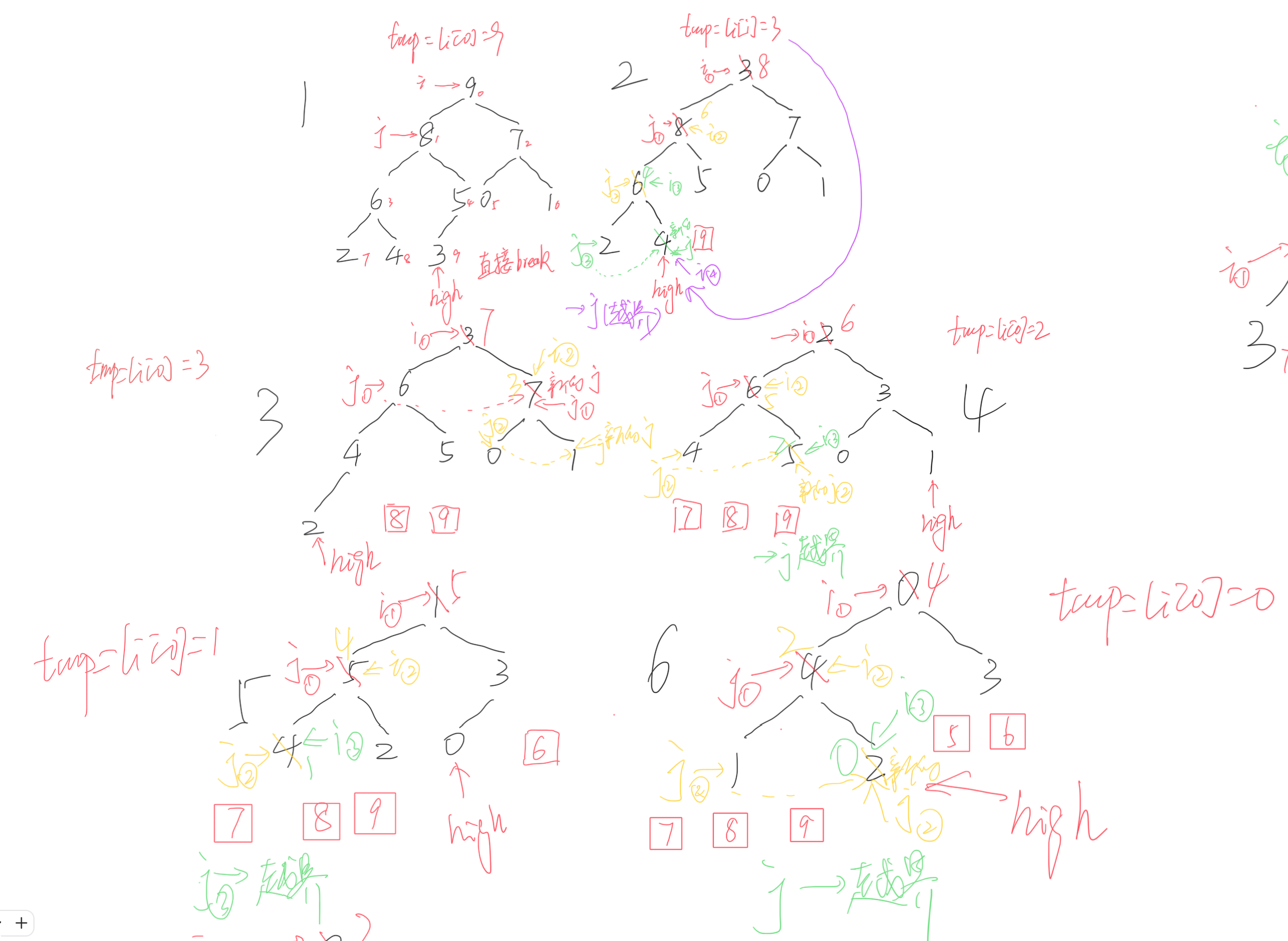
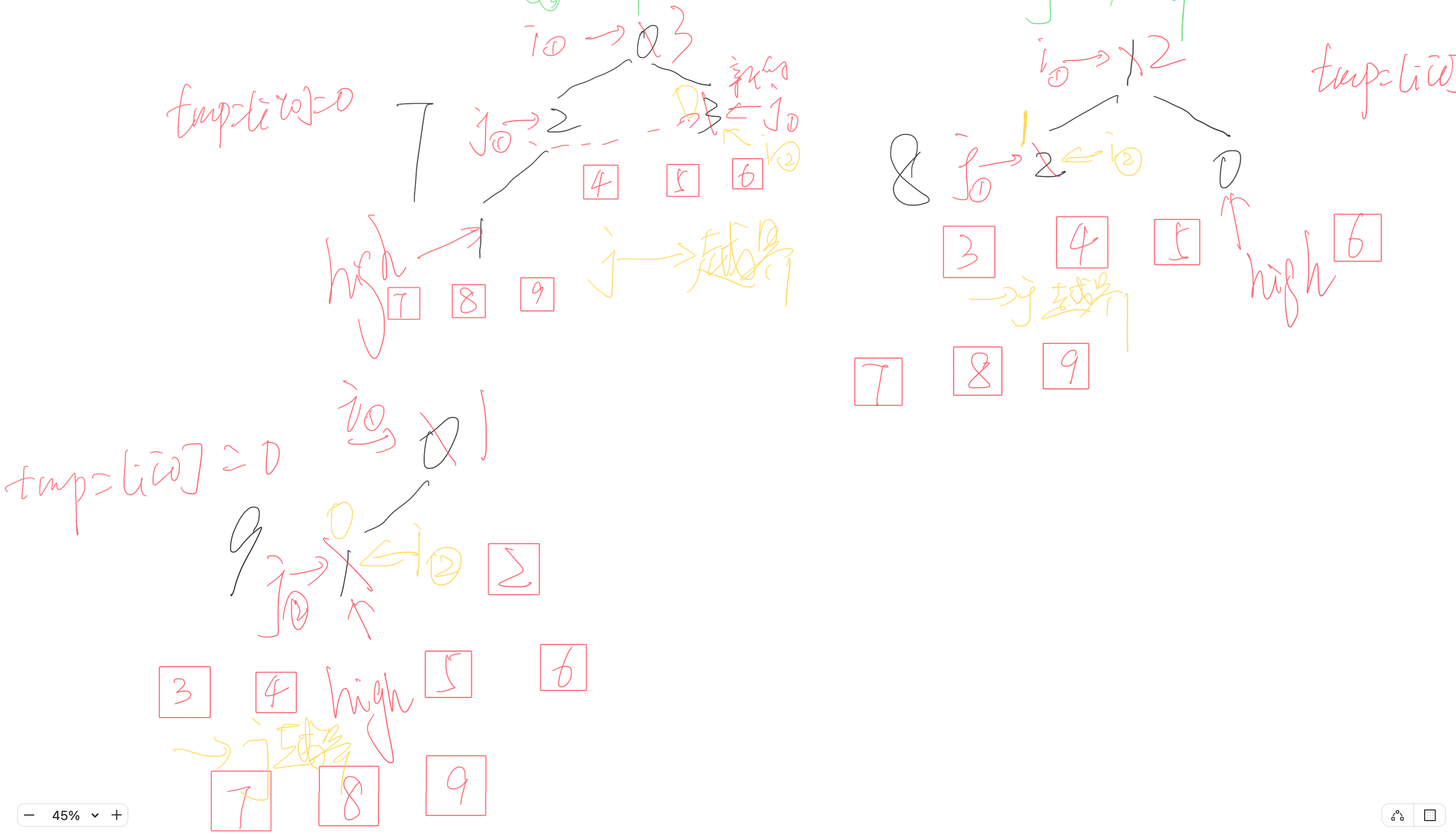
- 过程模拟
- 内容比较潦草,后期优化
- 根据代码运行过程详细记录了每一次建堆过程的运行情况
- i和j右下角的①②③④是移动的轮数
- j发出的虚线是右孩子的值比左孩子大,更新j的值
- 红色方框中的数是原堆顶的数,即有序序列
![]()
![]()
- 铺垫知识
-
6.归并排序
- 算法思想
- 分解:将一个大的序列越分越小,直至分成一个元素,单元素序列默认为有序
- 合并:从单元素序列开始,逐次将分解期间得到的序列归并,序列长度扩充,直到最终合并为一个有序序列
- Python代码
import random from cal_time import wrapper def merge(li, low, mid, high): # 假设列表分两段有序,逐步遍历两段合成一个有序列表 i = low j = mid + 1 li_tmp = [] while i <= mid and j <= high: # 只要左右两边都有数 if li[i] < li[j]: li_tmp.append(li[i]) i += 1 else: li_tmp.append(li[j]) j += 1 # while退出时,至少有一段序列遍历完毕 while i <= mid: li_tmp.append(li[i]) i += 1 while j <= high: li_tmp.append(li[j]) j += 1 li[low: high + 1] = li_tmp # 将暂存的有序序列再写回到原序列中 def _merge_sort(li, low, high): if low < high: # 至少有2个元素,递归 mid = (low + high) // 2 _merge_sort(li, low, mid) _merge_sort(li, mid + 1, high) merge(li, low, mid, high) @wrapper def merge_sort(li, low, high): _merge_sort(li, low, high) li = list(range(1000)) random.shuffle(li) print(li) merge_sort(li, 0, len(li) - 1) print(li)![]()
- C语言代码
#include <stdio.h> // 实现归并的过程,中间位置是mid void merge(int s[], int left, int mid, int right){ int i = left, j = mid + 1, k = 0; const int LEN = right - left + 1; char s_temp[LEN]; while(i <= mid && j <= right){ // 只要左右两个有序的子数组都有数 if(s[i] < s[j]){ s_temp[k++] = s[i++]; } else{ s_temp[k++] = s[j++]; } } // while执行完毕,至少有1个有序子数组遍历完成 while(i <= mid){ s_temp[k++] = s[i++]; } while(j <= right){ s_temp[k++] = s[j++]; } i = 0, j = left; while(i < LEN && j <= right ){ s[j] = s_temp[i]; i++; j++; } // 将暂存的有序数组再写回到原数组中 } // 使用归并的特征完成真正的排序 void merge_sort(int s[], int left, int right){ int mid; if(left < right){ // 只要数组中至少存在2个数就继续递归 mid = (left + right) / 2; merge_sort(s, left, mid); // 递归左边 merge_sort(s, mid + 1, right); // 递归右边 merge(s, left, mid, right); // 左边和右边合并 } } void print_arr(int s[], int n){ int i; for(i = 0; i < n; i++){ printf("%d ", s[i]); } } int main(){ int a[7], i; printf("请输入7个序列元素:\n"); for(i = 0; i < 7; i++){ scanf("%d", &a[i]); } printf("归并序前的序列为:"); print_arr(a, 7); merge_sort(a, 0, 6); printf("\n归并排序后的序列为:"); print_arr(a, 7); return 0; }![]()
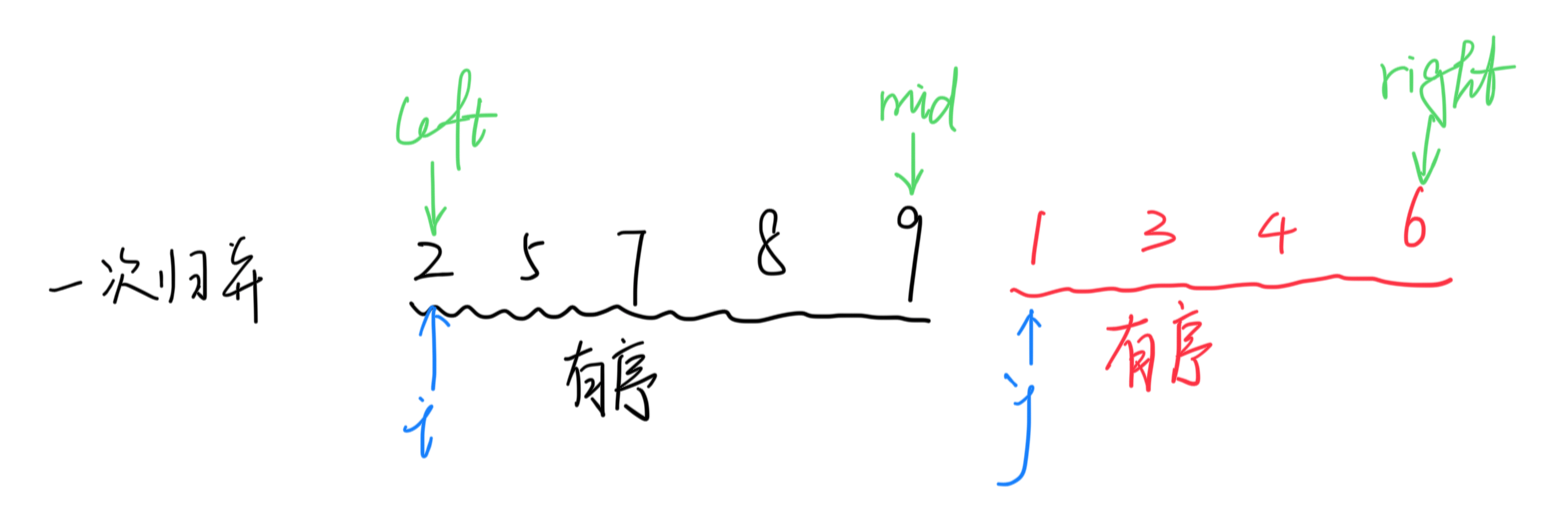
- 过程模拟
- 根据代码运行过程详细记录了递归调用与返回的运行情况
- 递归的层次通过不同颜色的方框区分
- 不同级别的标题也可表示不同深度的递归
![]()
![]()
![]()
- 算法思想
-
7.希尔排序
- 算法思想
- 0.希尔排序是一种特殊的分组插入排序算法
- 1.首先取1个整数d1 = n / 2,将元素分为d1个组,每组相邻两元素之间距离为d1,在各组内进行直接插入排序
- 2.接着取第2个整数d2 = d1 / 2,重复上述分组排序过程,直到di = 1,即所有元素在同一组内时,进行最后一次直接插入排序,此时序列即有效序列
- 注意:在希尔排序过程中,每排完一轮并不使某些元素有序,而是使整体数据越来越接近有序
- Python代码
import random from cal_time import wrapper def insert_sort_gap(li, gap): for i in range(gap, len(li)): tmp = li[i] j = i - gap while j >= 0 and li[j] > tmp: li[j + gap] = li[j] j -= gap li[j + gap] = tmp @wrapper def shell_sort(li): d = len(li) // 2 while d >= 1: insert_sort_gap(li, d) d = d // 2 li = list(range(10000)) random.shuffle(li) print(li) shell_sort(li1) print(li)![]()
- C语言代码
#include <stdio.h> void insert_sort_gap(int s[], int n, int gap){ int i, j, temp; for(i = gap; i < n; i++){ temp = s[i]; j = i - gap; while(j >= 0 && s[j] > temp){ s[j + gap] = s[j]; j -= gap; } s[j + gap] = temp; } } void shell_sort(int s[], int n){ int d = n / 2; while(d >= 1){ insert_sort_gap(s, n, d); d /= 2; } } void print_arr(int s[], int n){ int i; for(i = 0; i < n; i++){ printf("%d ", s[i]); } } int main(){ int a[7], i; printf("请输入7个序列元素:\n"); for(i = 0; i < 7; i++){ scanf("%d", &a[i]); } printf("希尔排序前的序列为:"); print_arr(a, 7); shell_sort(a, 7); printf("\n希尔排序后的序列为:"); print_arr(a, 7); return 0; }![]()
- 过程模拟
- 示例中d的值从分3组到分1组,相当于执行了2次shell_sort方法中的while循环
- j往左的虚线表示j的左移过程,temp的虚线表示temp赋值到合适的位置
- 当d为1,i指向8、9、14时未发生移动
![]()
- 算法思想
-
8.计数排序
- 算法思想
- 0.已知序列A中数的范围都在0到100之间,设计时间复杂度为O(n)的排序算法
- 1.将索引0-100在序列B对应位置的值初始化为0,每遍历到序列A中的某个数i,就将序列B中索引i对应位置的值加1,例如
- 序列A
- 数值:1 4 2 3 2 4 4 6 2
- 序列B
- 下标:0 1 2 3 4 5 6 下标为0-6是因为序列A中最大值为6
- 数值:0 1 3 1 3 0 1 数值为序列B下标值序列A的数值中出现的次数
- 序列A
- 2.依次遍历序列B的数值,假设某次得到数值i,则打印i对应的下标,共计i次。因为下标逐渐变大,得到的序列便是原序列A的有序排列
- Python代码
import random import copy from cal_time import wrapper @wrapper def count_sort(li, max_count=100): count = [0 for _ in range(max_count + 1)] for val in li: count[val] += 1 li.clear() for ind, val in enumerate(count): # enumerate 将下标和值做了对应 for i in range(val): li.append(ind) @wrapper def sys_sort(li): li.sort() li = [random.randint(0, 100) for _ in range(10000)] li1 = copy.deepcopy(li) li2 = copy.deepcopy(li) count_sort(li1) sys_sort(li2) print(li1)![]()
- C语言代码
#include <stdio.h> #include <stdlib.h> #include <time.h> #define MAX 300 void print_arr(int s[], int n){ int i; for(i = 0; i < n; i++){ printf("%d ", s[i]); } } void set_zero(int s[], int n){ int i; for(i = 0; i < n; i++){ s[i] = 0; } } void count_sort(int s[], int c[], int m){ int i = 0, index, times; for(index = 0; index < m; index++){ times = c[index]; while(times != 0){ s[i++] = index; times--; } } } int main(){ int s[MAX] = {0}, count[101] = {0}, i; srand(time(NULL)); for(i = 0; i < MAX; i++){ s[i] = rand() % 101; count[s[i]]++; } set_zero(s, MAX); count_sort(s, count, 101); print_arr(s, MAX); return 0; }![]()
- 过程模拟
![]()
- 算法思想
-
9.桶排序
- 算法思想
- 0.在计数排序中,如果元素的范围比较大(比如在1到1亿之间)则算法效率显著降低,如何改造算法?
- 1.可以先将元素分在不同的桶中,再对每个桶中的元素排序
- 注意:桶排序用的不多,重要性低于前面几种排序方法;桶排序的表现取决于数据的分布,对不同的数据排序时需要采取不同的分桶策略
- Python代码
import random from cal_time import wrapper @wrapper def bucket_sort(li, n=100, max_num=10000): # n表示桶的数量,数据的最大值为10000 buckets = [[] for _ in range(n)] # 创建桶 for var in li: # 桶号范围为0 ~ n - 1,max_num/n的值是桶的数量,i表示var放到几号桶里 # 9999放到99号桶里,当var=10000时越界,没有100号桶,所以放到99号桶 i = min(var // (max_num // n), n - 1) buckets[i].append(var) # 将var加到桶中 # 追加一个数后,通过冒泡排序的过程保持桶内的顺序 # 从桶中最后一个元素开始与前面的元素比,一直到数组中下标为1的数 for j in range(len(buckets[i]) - 1, 0, -1): if buckets[i][j] < buckets[i][j - 1]: buckets[i][j], buckets[i][j - 1] = buckets[i][j - 1], buckets[i][j] else: break sorted_li = [] for buc in buckets: sorted_li.extend(buc) return sorted_li li = [random.randint(0, 10000) for i in range(100000)] li = bucket_sort(li) print(li)![]()
- C语言代码
- 算法思想
-
10.基数排序
- 算法思想
- Python代码
- C语言代码







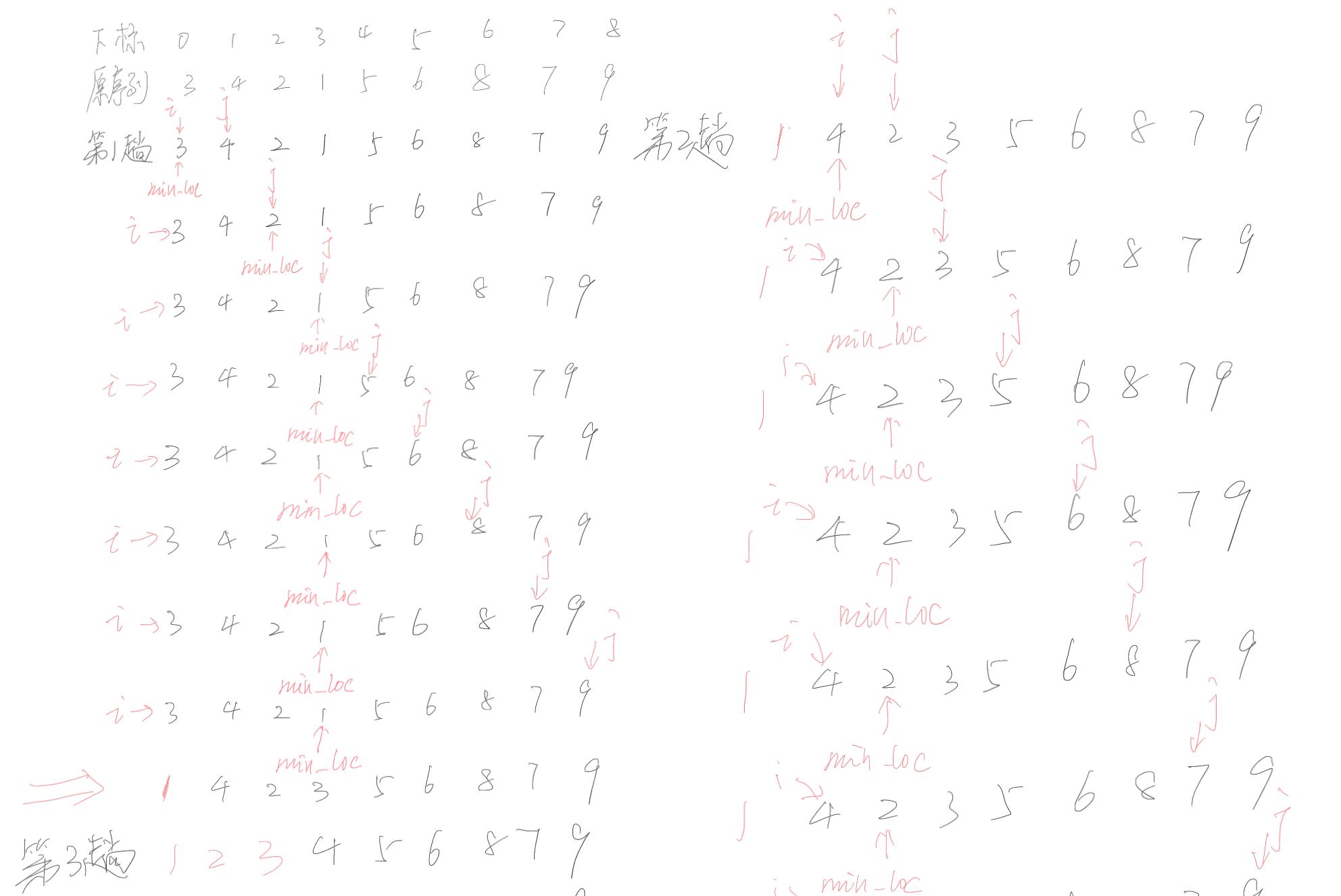





















 浙公网安备 33010602011771号
浙公网安备 33010602011771号