FIR滤波器的FPGA实现和matlab验证(一)
参考资料
视频
文章
个人思维
数字滤波器从实现结构上划分,有FIR和IIR两种。FIR的特点是:线性相位、消耗资源多;
IIR的特点是:非线性相位、消耗资源少。
由于FIR系统的线性相位特点,设计中绝大多数情况都采用FIR滤波器。
何为线性相位?
指在用户关心的频带内,LTI系统满足线性相位要求:
- 从延时的角度来看,输入的相位响应是线性的,即保证了输入信号的延时特性
- 从相位的角度来看,输入的各频率成分信号之间,相对相位是固定的,通过了线性相位系统,其响应信号的相对相位关系不变
对于关心相位的系统,比如调制解调系统,需要使用FIR滤波器;对于只关心频率成分的系统,比如只是提取某一频率分量,为了节省资源,使用IIR滤波器即可。
FIR滤波器
Finite Impulse Response有限长单位冲激响应滤波器,又称为非递归型滤波器
FIR 滤波器具有严格的线性相频特性,同时其单位响应是有限长的,因而是稳定的系统,在数字通信、图像处理等领域都有着广泛的应用。

FIR 滤波器本质上就是输入信号与单位冲击响应函数的卷积,表达式如下(N为滤波器的阶数,其滤波系数为N+1,即为抽头数TAP,阶次越高,滤波效果就越好)
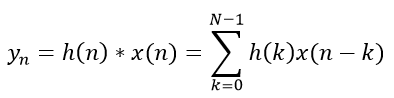
x(n)是我们的待滤波信号,h(n)是滤波器系数(冲激响应)。卷积的过程其实就是一个乘、累加的过程。
FIR滤波器特性
-
响应是有限长序列
-
系统函数在\(|z|>0\)处收敛,极点全部在z=0处,属于因果系统
-
结构上是非递归,即没有输出到输入的反馈
-
输入信号相位响应是线性的,因此响应函数\(h(n)\)系数是对称的(只有当FIR的h(n)对称时,FIR滤波器才具有线性相位特性)
-
FIR滤波器分为奇对称和偶对称。也就是当滤波器的阶数为3时,更具线性相位对称法则,h(0)=h(3),h(1)=h(2)
-
可得到方程式为:
\[y(n)=h(0) \{x(n-1)+x(0)\}+h(1)\{x(n-2)+x(1))\} \] -
当滤波器阶数为奇数n=4时,根据线性相位跟对称法则可得:h(0)=h(4),h(1)=h(3),h(2)独立一个
-
可得方程式为
\[y(n)=h(0)\{x(n-1)+x(0)\}+h(1)\{x(n-2)+x(n-3)\}+h(2)x(n-2) \] -
故系统函数为
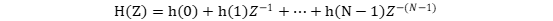
-
-
输入信号的各频率之间,相对相位差也是固定不变的
-
时域卷积等于频率相乘,因此该卷积相当于筛选频谱中各频率分量的增益倍数。某些频率分量保留,某些频率分量衰减,从而实现滤波的效果。
FIR滤波器设计
实现FIR滤波器的过程其实就是卷积的过程,卷积的公式如上。FIR滤波器是由一个抽头的延迟线加法器和乘法器构成的,每个乘法器的操作系数是FIR滤波器系数。卷积的过程其实就是一个乘、累加的过程。
所以用FPGA实现8阶FIR滤波器的主要分为三级流水线。
按照三级流水线实现FIR滤波器设计:信号延迟-系数相乘-求和
Verilog代码如下(很基础的版本,不考虑时序问题)
module fir_guide
#(parameter width = 8)
(
input CLK,
input RSTn,
input [width-1:0] din,
output reg [2*width-1:0] dout
);
//data on delay
reg[7:0] delay_pipeline1 ;
reg[7:0] delay_pipeline2 ;
reg[7:0] delay_pipeline3 ;
reg[7:0] delay_pipeline4 ;
reg[7:0] delay_pipeline5 ;
reg[7:0] delay_pipeline6 ;
reg[7:0] delay_pipeline7 ;
reg[7:0] delay_pipeline8 ;
reg[7:0] delay_pipeline9 ;
always@(posedge CLK or negedge RSTn)
if(!RSTn)
begin
delay_pipeline1 <= 8'b0 ;
delay_pipeline2 <= 8'b0 ;
delay_pipeline3 <= 8'b0 ;
delay_pipeline4 <= 8'b0 ;
delay_pipeline5 <= 8'b0 ;
delay_pipeline6 <= 8'b0 ;
delay_pipeline7 <= 8'b0 ;
delay_pipeline8 <= 8'b0 ;
delay_pipeline9 <= 8'b0 ;
end
else
begin
delay_pipeline1 <= din ;
delay_pipeline2 <= delay_pipeline1 ;
delay_pipeline3 <= delay_pipeline2 ;
delay_pipeline4 <= delay_pipeline3 ;
delay_pipeline5 <= delay_pipeline4 ;
delay_pipeline6 <= delay_pipeline5 ;
delay_pipeline7 <= delay_pipeline6 ;
delay_pipeline8 <= delay_pipeline7 ;
delay_pipeline9 <= delay_pipeline8 ;
end
//mult
wire[7:0] coeff1 = 8'd7; //滤波器系数
wire[7:0] coeff2 = 8'd5;
wire[7:0] coeff3 = 8'd51;
wire[7:0] coeff4 = 8'd135;
wire[7:0] coeff5 = 8'd179;
wire[7:0] coeff6 = 8'd135;
wire[7:0] coeff7 = 8'd51;
wire[7:0] coeff8 = 8'd5;
wire[7:0] coeff9 = 8'd7;
reg signed [16:0] multi_data1 ;//乘积结果
reg signed [16:0] multi_data2 ;
reg signed [16:0] multi_data3 ;
reg signed [16:0] multi_data4 ;
reg signed [16:0] multi_data5 ;
reg signed [16:0] multi_data6 ;
reg signed [16:0] multi_data7 ;
reg signed [16:0] multi_data8 ;
reg signed [16:0] multi_data9 ;
always@(posedge CLK or negedge RSTn) //x(0) * h(0)
if(!RSTn)
multi_data1 <= 17'b0 ;
else
multi_data1 <= delay_pipeline1*coeff1 ;
always@(posedge CLK or negedge RSTn) //x(1) * h(1)
if(!RSTn)
multi_data2 <= 17'b0 ;
else
multi_data2 <= delay_pipeline2*coeff2 ;
always@(posedge CLK or negedge RSTn) //x(2) * h(2)
if(!RSTn)
multi_data3 <= 17'b0 ;
else
multi_data3 <= delay_pipeline3*coeff3 ;
always@(posedge CLK or negedge RSTn) //x(3) * h(3)
if(!RSTn)
multi_data4 <= 17'b0 ;
else
multi_data4 <= delay_pipeline4*coeff4 ;
always@(posedge CLK or negedge RSTn) //x(4) * h(4)
if(!RSTn)
multi_data5 <= 17'b0 ;
else
multi_data5 <= delay_pipeline5*coeff5 ;
always@(posedge CLK or negedge RSTn) //x(5) * h(5)
if(!RSTn)
multi_data6 <= 17'b0 ;
else
multi_data6 <= delay_pipeline6*coeff6 ;
always@(posedge CLK or negedge RSTn) //x(6) * h(6)
if(!RSTn)
multi_data7 <= 17'b0 ;
else
multi_data7 <= delay_pipeline7*coeff7 ;
always@(posedge CLK or negedge RSTn) //x(7) * h(7)
if(!RSTn)
multi_data8 <= 17'b0 ;
else
multi_data8 <= delay_pipeline8*coeff8 ;
always@(posedge CLK or negedge RSTn) //x(8) * h(8)
if(!RSTn)
multi_data9 <= 17'b0 ;
else
multi_data9 <= delay_pipeline9*coeff9 ;
//===================================================================
//加法器
//===================================================================
always@(posedge CLK or negedge RSTn)
if(!RSTn)
dout <= 16'b0 ;
else
dout <= multi_data1 + multi_data2 + multi_data3 + multi_data4 +multi_data5 + multi_data6 + multi_data7 + multi_data8 + multi_data9 ;
endmodule
然后开始写testbench文件,需要输入一个波形,此处用matlab去生成一个想要的波形
本设计用于仿真的输入波形是三个正弦波叠加而成,分别是1KHZ、3KHZ、4KHZ。下面是用于生成待滤波信号的m文件内容:
%*********产生.data文件 用于FPGA仿真************%
Fs = 10000; %采样频率决定了两个正弦波点之间的间隔
N = 4096; %采样点数
N1 = 0 : 1/Fs : N/Fs-1/Fs;
s = sin(1000*2*pi*N1) + sin(3000*2*pi*N1) +sin(4000*2*pi*N1);//三种正弦波
fidc = fopen('D:\my_profile\fpga_project\matlab_prj\mem.txt','wt'); //将结果写入mem.txt文件,便于modesim使用
for x = 1 : N
fprintf(fidc,'%x\n',round((s(x)+2.12)*58));//取整,并且置为正
end
fclose (fidc);
设计完成后用quartus和modelsim进行联合仿真
此时的testbench文件代码如下:
`timescale 1ps/1ps
module test();
reg CLK;
reg [7:0] FIR_IN;
reg RSTn;
reg [7:0] mem[1:4096];
wire [15:0] FIR_OUT;
reg [12:0] i;
fir_guide i1 (
.CLK(CLK),
.din(FIR_IN),
.dout(FIR_OUT),
.RSTn(RSTn)
);
initial
begin
$readmemh("D:/my_profile/fpga_project/matlab_prj/mem.txt",mem);//将待滤波信号读入mem
RSTn= 0;
CLK= 0;
#50;
RSTn= 1;
#50000;
$stop;
end
initial
forever
#10 CLK = ~CLK;
always@(posedge CLK or negedge RSTn)
if(!RSTn)
FIR_IN <= 8'b0 ;
else
FIR_IN <= mem[i];
always@(posedge CLK or negedge RSTn)
if(!RSTn)
i <= 12'd0;
else
i <= i + 1'd1;
endmodule
出来的波形为
- 用matlab去验证波形是否正确
%脚本文件验证FIR滤波的可行性%
Fs = 10000; %采样频率决定了两个正弦波点之间的间隔
N = 4096; %采样点数
N1 = 0 : 1/Fs :N/Fs-1/Fs;
in =sin(1000*2*pi*N1) + sin(3000*2*pi*N1) + sin(4000*2*pi*N1);
coeff =[-0.0325,-0.0384,0.0784,0.2874,0.3984,0.2874,0.0784,-0.0384,-0.0325];
out =conv(in,coeff);%卷积滤波
subplot(2,1,1);
plot(in);
xlabel('滤波前');
axis([0 200 -3 3]);
subplot(2,1,2);
plot(out);
xlabel('滤波后');
axis([100 200 -2 2]);

即得证。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号