【学习笔记】笛卡尔树

简介

笛卡尔树是一种树状数据结构。具体地，该数的每一个节点储存的是一个二元组信息 \((k,x)\)，其中，如果只看 \(k\) 这一个元素的话满足BST的性质，如果只看 \(x\) 一个元素，满足堆的性质。然后我放一张图来便于理解。

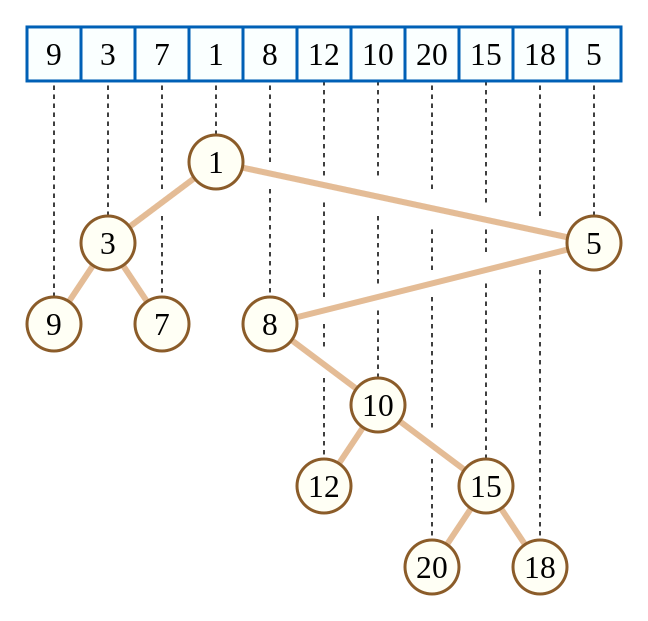
上图就是一个典型的笛卡尔树。

建树（Luogu P5854）

首先宣布一个很令人吃惊的信息，笛卡尔树建树可以做到 \(O(n)\) ！！！

那么具体怎么来建树呢？我们考虑维护笛卡尔树的右链，所谓右链，即从根一直向右儿子延伸的一条链。容易发现右链上元素都是递增的，下标也是递增的，我们容易用一个单调栈来维护右链。

考虑加入新点，设当前位置为 \(i\)，我们可以找到右链上第一个小于 \(a_i\) 的元素，然后将 \(i\) 变为那个位置的右儿子，那他之前的右儿子怎么办呢，直接接到 \(i\) 的左儿子上即可，手摸一下容易发现这是一定正确的。然后还有一张图可以解释清这其中的一些流程。

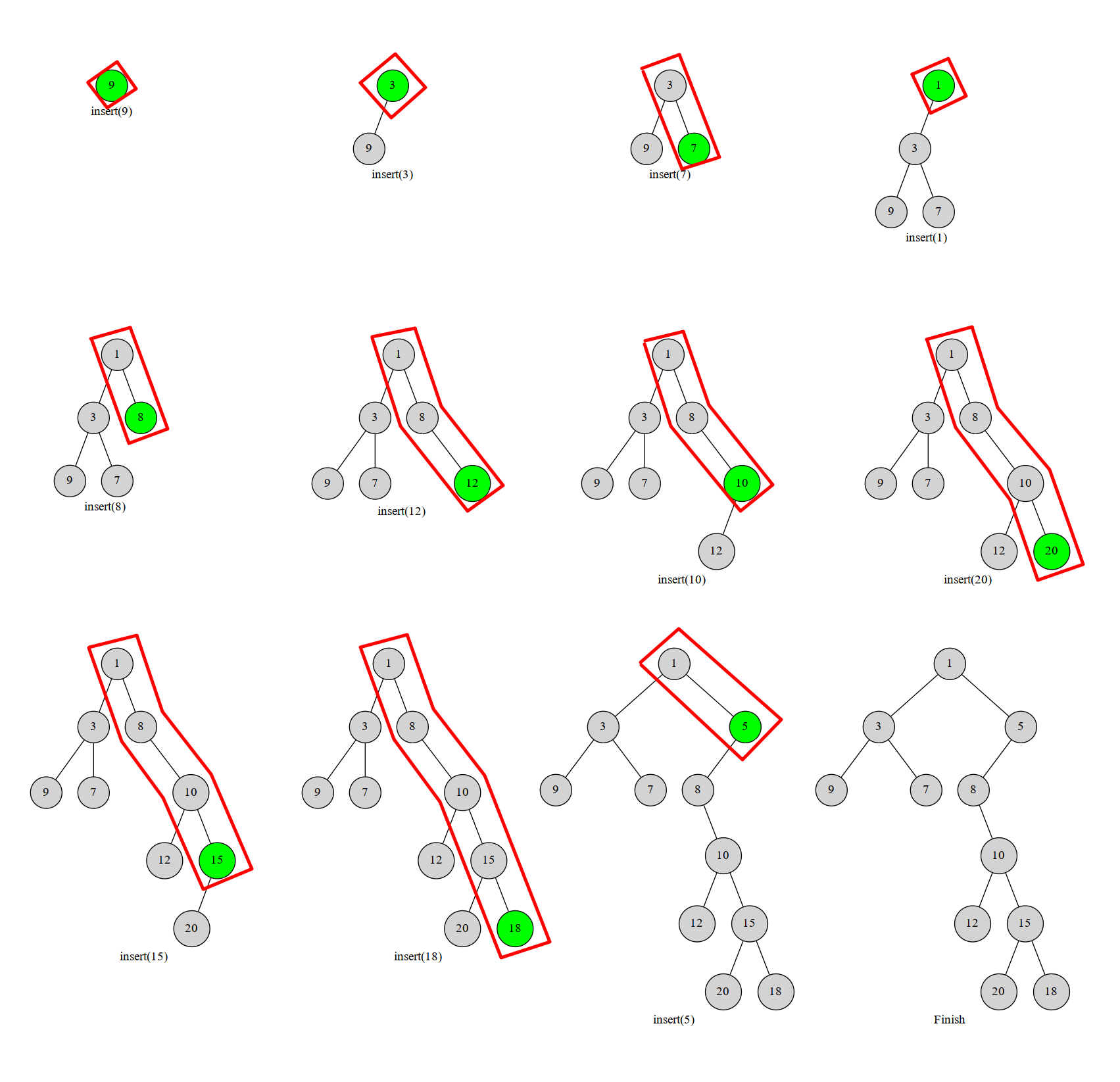
具体地，可以这样实现。

for(int i = 1;i <= n;i ++)
{
	int k = top;
	while(k && a[stk[k]] > a[i]) k --;
	if(k) rs[stk[k]] = i;
	if(k < top) ls[i] = stk[k + 1];
	stk[++ k] = i;top = k;
}

与dp之间的关系

这一部分还需要多多积累，现在也就知道了一个这样的题，还是来记录一下。

P6453 [COCI2008-2009#4] PERIODNI

由于这个题的限制相当奇怪，之间有缺口的地方又是合法的，所以一种低级的计数思路是分治，具体地，如下图一样分成若干个矩形。

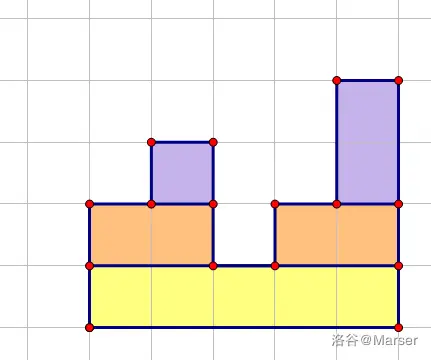
仔细观察后容易得到其实这里的每一个矩形实际都和以 \(h_i\) 建立的小根笛卡尔树上的某一个节点一一对应。

具体地，对于笛卡尔树上节点 \(u\),所对应的矩形长度为 \(siz_u\) , 高度为 \(h_u-h_{fa}\)。

对于笛卡尔树上的某一个节点 \(u\),记 \(siz_u\) 表示该点子树大小。

这时我们考虑DP，设 \(dp_{u,i}\) 表示树上节点 \(u\) 子树代表的图形内选了 \(i\) 个节点的方案数。

考虑如何转移，设 \(u\) 所代表的矩形外选了 \(j\) 个点，那么此时 \(dp_{u,i}=f(u,i) + \sum f(u,j)\times C_{siz_u-j}^{i-j}\times C_{h_u-h_{fa}}^{i-j}\times (i-j)!\)。

\(f(u,j)\) 表示 \(u\) 子树内除 \(u\) 以外的节点所选的点数为 \(j\) 的方案数。