●小集训之旅 二

有志者自有千计万计，无志者只感千难万难。

●2017.3.28-29

●学习内容：伸展树 Splay Tree

引：二叉查找树(Binary Search Tree) 可以被用来表示有序集合、建立索引或优先队列等。最坏情况下，作用于二叉查找树上的基本操作的时间复杂度，可能达到O(n)。

●伸展树(Splay Tree)是二叉查找树的改进。

优点：对伸展树的操作的平摊复杂度是O(log2n)。伸展树的空间要求较低。

在伸展树上的一般操作都基于伸展操作：假设想要对一个二叉查找树执行一系列的操作，为了使整个操作时间更小，被操作频率高的那些节点（子树）就应当经常处于靠近树根的位置。于是在每次操作之后对树进行重构，把被操作的节点（子树）搬移到离树根近一些的地方（并保证不破坏二叉树中各节点之间的关系）。伸展树应运而生。伸展树是一种自调整形式的二叉查找树，它会沿着从某个节点到树根之间的路径，通过一系列的旋转把这个节点搬移到树根去。

（我们的Y老师曰：这是一种“玄学”算法，学了以后我感觉很有道理。）

（我们的Y老师还曰：Splay Tree是“区间王”，学了以后我也感觉很有道理。）

●算法相关内容(基础与支持操作)

    • 单旋与双旋 rotate（）（通过旋转操作使得x成为root）
      • 单旋：在操作完位于节点x之后，对x进行旋转操作，使得x的父亲节点成为x的儿子节点 下面是两种情况：（x的父亲节点y是root，即fa[x]==y==root）
  • 单旋图 
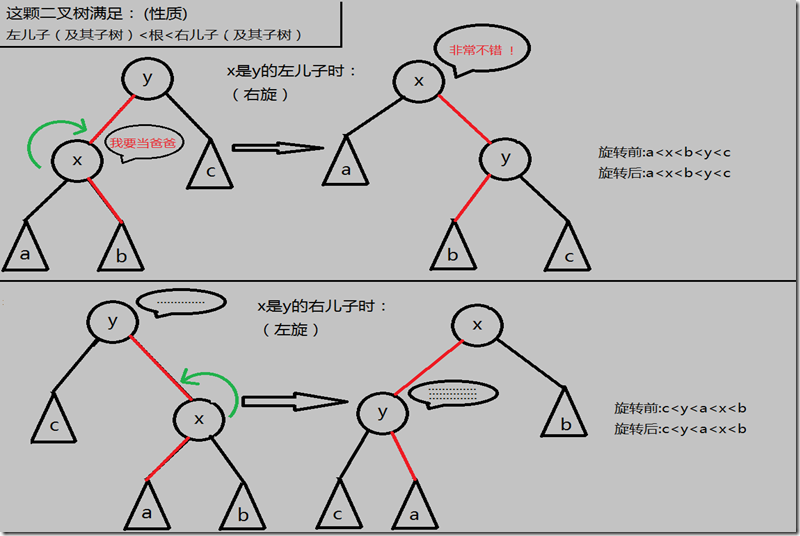
    • 所以：
  • 单旋图结论
    • 双旋：当x的父节点y的父节点z是根时，即fa[ fa[x] ]==z==root，则为了将x变为root，要进行两次旋转，那么便要分为两种情况来操作：（初学者当结论记吧，Y老师说是“玄学”）
      • 同侧情况（即 x和y都为其父亲的左儿子或右儿子）

                           则先旋转y，再旋转x：（右旋—右旋 or 左旋—左旋）

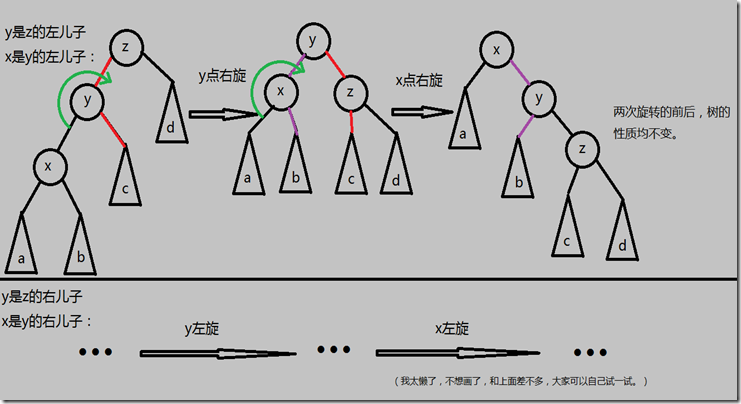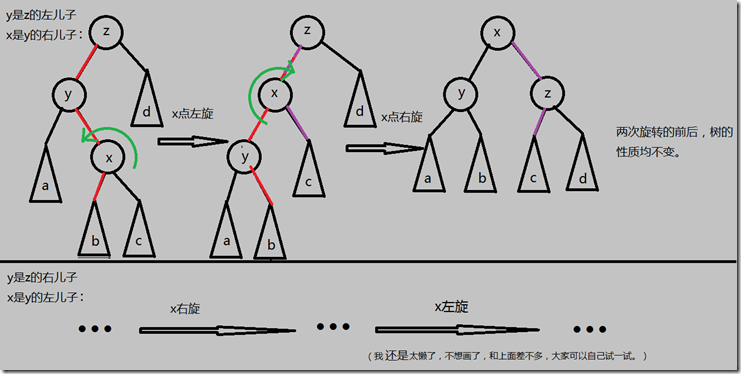
      • 双旋一图（直接由上面的两次单旋构成，每次关系变化的边只有两条，只是每次对象不同）
      • 异侧情况（即x和y分别为其父亲的左儿子和右儿子）

                          则对x进行两次旋转：（左旋—右旋 or 右旋—左旋）

        • 双旋二图（也是由上面的两次单旋过程，且每次的对象相同，只是第一次关系变化的边有三条。第二次关系变化的边任只有两条。）
        • 有了上面的单旋和双旋的操作，便可把任意位置的x点移动到root的位置 (如何移动见下文； 为什么双旋要这样旋，额，我还不太明白具体原因，我先当结论记吧，Y老师说是“玄学”，不好证明。)
      • Splay（）函数（“伸展运动”）
        • 该函数的目的便是通过调用rotate（）旋转函数，实现把x旋转到root位置（~也可以到其他位置），代码如下（学习hzwer的)
void rotate(int x,int &k)											//旋转（单） 
{
	int y=fa[x],z=fa[y];
	int l=(x!=c[y][0]),r=l^1;
	if(y==k) k=x;
	else c[z][y!=c[z][0]]=x;
	fa[x]=z; fa[y]=x; fa[c[x][r]]=y;
	c[y][l]=c[x][r]; c[x][r]=y;
	update(y); update(x);
}

void splay(int x,int &k)		//伸展运动 ，e 
{
	int y,z;
	while(x!=k)
	{
		y=fa[x],z=fa[y];
		if(y!=k)
		{
			if(c[y][0]==x^c[z][0]==y) rotate(x,k);
			else rotate(y,k);
		}
		rotate(x,k);
	}
}
        • 有了以上的两个函数，那么伸展树基础便有了；下面说说其为“区间王”的原由
      • Split（）函数
        • 看图:
        • Split图
        • 有了这一函数，需要操作的区间便被单独放入了root的右儿子的左儿子所在的子树中，我们就可以对该子树的根进行操作，添加lazy标记之类的，就可以解决很多区间问题。（比线段树更强）
      • find（）函数
        • 上图中，我们把区间形成一棵单独的子树的前提是要找到区间两侧的外端点（的编号），才能对其进行Splay（）操作，移到根节点或根的右儿子节点。
        • 如何在树中找到我们要的点（的编号）呢（即原序列中的第几个点）,代码如下，（不难。）
int find(int k,int x)//找树中的目标点 
{
	pushdown(k);
	if(siz[c[k][0]]+1==x) return k; 
	if(siz[c[k][0]]>=x) return find(c[k][0],x);
	else return find(c[k][1],x-siz[c[k][0]]-1);
}
int split(int k,int len)//裂（把需要的区间弄到根的右儿子的左儿子所在的子树上c[c[rt][1]][0]） 
{					                        
	int x=find(rt,k),y=find(rt,k+len+1);
	splay(x,rt);splay(y,c[x][1]);
	return c[y][0];
}
        • （Ps：代码中的pushdown（）是为了将lazy标记传下去。）
      • 其它函数（build(),insert(),rever(),erase(),rec(),modify()……）
        • 有了之前的那些函数，结合lazy标记，那么区间操作就方便极了
        • （只是要注意在区间操作时的，每次树的形态改变之前，一定要把lazy标记传下去）
      • 下面以一个题来”奉上“众多函数
        • (NOI 2005 维修数列（bzoj 1500 )）
        • 题图：
        • NOI 2005 维修数列
        • 此题涵盖了不少函数，是一个很好的”裸题”，直接上代码了；（学习hzwer的）
#include<queue>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define inf 1000000000
#define N 1000005
using namespace std;
int read()//读入优化 
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
int n,m,rt,cnt,k,len,val; char ch[10];
int a[N],id[N],fa[N],c[N][2];
int sum[N],siz[N],v[N],mx[N],lx[N],rx[N];
bool tag[N],rev[N];
queue<int> q;
void update(int x)                                            
{
	int l=c[x][0],r=c[x][1];
	sum[x]=sum[l]+sum[r]+v[x];
	siz[x]=siz[l]+siz[r]+1;
	mx[x]=max(mx[l],mx[r]);
	mx[x]=max(mx[x],rx[l]+v[x]+lx[r]);
	lx[x]=max(lx[l],sum[l]+v[x]+lx[r]);
	rx[x]=max(rx[r],sum[r]+v[x]+rx[l]);
}
void pushdown(int x)                                          
{
	int l=c[x][0],r=c[x][1];
	if(tag[x])
	{
		rev[x]=tag[x]=0;                         //有tag 就不 rev 
		if(l) tag[l]=1,v[l]=v[x],sum[l]=v[l]*siz[l];
		if(r) tag[r]=1,v[r]=v[x],sum[r]=v[r]*siz[r];
		if(v[x]>=0)
		{
			if(l) lx[l]=rx[l]=mx[l]=sum[l];
			if(r) lx[r]=rx[r]=mx[r]=sum[r];
		}
		else 
		{
			if(l)lx[l]=rx[l]=0,mx[l]=v[x];
			if(r)lx[r]=rx[r]=0,mx[r]=v[x];
		}
	}
	if(rev[x])
	{
		rev[x]^=1;rev[l]^=1;rev[r]^=1;          //(^ 的妙处 )
 		swap(lx[l],rx[l]);swap(lx[r],rx[r]); 
		swap(c[l][0],c[l][1]);swap(c[r][0],c[r][1]);
	}
}
void rotate(int x,int &k)//旋转（单） 
{
	int y=fa[x],z=fa[y];
	int l=(x!=c[y][0]),r=l^1;
	if(y==k) k=x;
	else c[z][y!=c[z][0]]=x;
	fa[x]=z; fa[y]=x; fa[c[x][r]]=y;
	c[y][l]=c[x][r]; c[x][r]=y;
	update(y); update(x);
}
void splay(int x,int &k)//伸展运动 ，e 
{
	int y,z;
	while(x!=k)
	{
		y=fa[x],z=fa[y];
		if(y!=k)
		{
			if(c[y][0]==x^c[z][0]==y) rotate(x,k);
			else rotate(y,k);
		}
		rotate(x,k);
	}
}
void build(int l,int r,int f)//建树 
{
	if(l>r) return;
	int mid=l+r>>1,now=id[mid],last=id[f];
	if(l==r)
	{
		sum[now]=a[l];
		siz[now]=1;
		tag[now]=rev[now]=0;
		if(a[l]>=0)lx[now]=rx[now]=mx[now]=a[l];
		else lx[now]=rx[now]=0,mx[now]=a[l];
	}
	build(l,mid-1,mid);build(mid+1,r,mid);
	v[now]=a[mid];
	fa[now]=last;
	c[last][mid>=f]=now;
	update(now);
}
int find(int k,int x)//找树中的目标点 
{
	pushdown(k);
	if(siz[c[k][0]]+1==x) return k; 
	if(siz[c[k][0]]>=x) return find(c[k][0],x);
	else return find(c[k][1],x-siz[c[k][0]]-1);
}
int split(int k,int len)//裂（把需要的区间弄到根的右儿子的左儿子所在的子树上c[c[rt][1]][0]） 
{																									
	int x=find(rt,k),y=find(rt,k+len+1);
	splay(x,rt);splay(y,c[x][1]);
	return c[y][0];
}
void insert(int k,int len)//插入 
{
	for(int i=1;i<=len;i++)
	if(!q.empty()) id[i]=q.front(),q.pop();
	else id[i]=++cnt;
	for(int i=1;i<=len;i++) a[i]=read();
	build(1,len,0);
	int x=id[1+len>>1];
	int z=find(rt,k+1),y=find(rt,k+2);//第一位为-inf 
	splay(z,rt); splay(y,c[z][1]);
	fa[x]=y; c[y][0]=x;
	update(y);update(fa[y]);
}
void rec(int x)//删除时“回收空间”	（把不要的点的编号放进队列，下次要加新点时，直接用队列里的编号） 
{															
	if(!x) return;
	int l=c[x][0],r=c[x][1];
	rec(l); rec(r);
	q.push(x);
	fa[x]=c[x][0]=c[x][1]=0;
	tag[x]=rev[x]=0;
}
void erase(int k,int len)//删除区间 
{
	int x=split(k,len),y=fa[x];
	rec(x); c[y][0]=0;
	update(y);update(fa[y]);
}
void query(int k,int len)//询问区间和 
{
	int x=split(k,len);
	printf("%d\n",sum[x]);
}
void rever(int k,int len)//区间翻转 
{
	int x=split(k,len),y=fa[x];
	if(!tag[x])
	{
		rev[x]^=1;						// ^ 的妙处 
		swap(lx[x],rx[x]);
		swap(c[x][0],c[x][1]);
		update(y);update(fa[y]);
	}
}
void modify(int k,int len,int val)//区间修改 
{
	int x=split(k,len),y=fa[x];
	tag[x]=1; v[x]=val;
	sum[x]=v[x]*siz[x];
	if(v[x]>=0) lx[x]=rx[x]=mx[x]=sum[x];
	else lx[x]=rx[x]=0,mx[x]=v[x];
	update(y);update(fa[y]);
}
int main()
{
	n=read();m=read();
	mx[0]=a[1]=a[n+2]=-inf; id[1]=1; id[n+2]=n+2;
	for(int i=2;i<=n+1;i++) a[i]=read(),id[i]=i;
	build(1,n+2,0);
	rt=n+3>>1; cnt=n+2;
	while(m-->0)
	{
		scanf("%s",ch);
		if(ch[0]!='M'||ch[2]!='X') k=read(),len=read();
		if(ch[0]=='I') insert(k,len);
		if(ch[0]=='D') erase(k,len);
		if(ch[0]=='R') rever(k,len);
		if(ch[0]=='G') query(k,len);
		if(ch[0]=='M')
		{
			if(ch[2]=='X')printf("%d\n",mx[rt]);
			else val=read(),modify(k,len,val);
		}
	}
	return 0;
}
/* 
	●需要 update() 的地方：                                  
	  build(), rotate(), modify(), rever(), erase(), insert();
	●需要 pushdown() 的地方：
	  程序中似乎只有 find() 中调用了pushdown()，
	  但众多操作中都通过  split()-->find()-->pushdown()来间接调用了pushdown()
	  ○调用pushdown()的原则：在树的形态发生变化前要把lazy标记传下去；
	    （split()中会调用splay(),使树的形态发生改变，所以split()中要先通过find()把lazy标记传下去） 
	 */

●总结：该算法的区间操作能力强大，时间空间也都比较优秀，无愧于“区间王”，但仍然有小小一点缺陷：1.常数过大，容易被卡。2.代码长，函数多，容易打错，所以要多多练习，把这些函数打熟练。

posted @ 2017-03-29 15:47  *ZJ  阅读(174)  评论(1)    收藏  举报