浅谈一下图像卷积后的大小推理和几种网络的大致结构

怎么知道一张图片经过滤波器处理后的大小（神经网络中）？
假设输入大小为(H,W),滤波器大小为(FH,FW),输出大小为(OH,OW),填充是P,步幅是S。则经过此滤波器后，图像的大小为

\[OH=\frac{H+2 P-F H}{S}+1 \]

\[OW=\frac{W+2 P-F W}{S}+1 \]

上式主要体现在网络中的卷积层，池化层公式一样
注：当除不尽，即当有小数时咋办，不同深度学习的框架处理不一样，在Pytorch中，会直接将最后一行以及最后一列忽略掉，以保留整数尽，即向下取整

接着胡说一下各网络吧！
1、首先就是那鼻祖，大哥大LeNet，直接上图

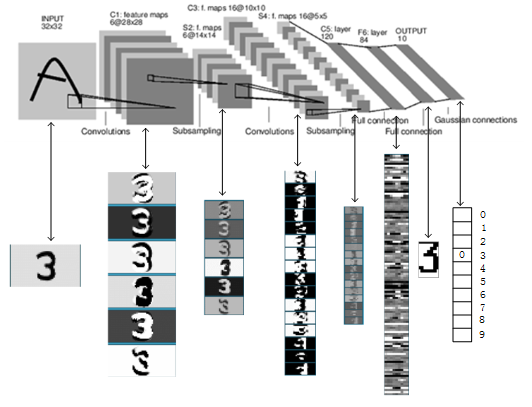
这兄弟浅显易懂，至于尺寸根据上面的公式就可以得出，这里说明一下，它使用5×5的滤波器(步幅为1)，2×2的池化(步幅为2)

• 另外，它用Sigmoid，而现在主要是Relu，为啥，其中一个说是Relu能使网络训练更快收敛，这里所说的收敛我想应该是网络损失函数的值趋于稳定，为啥更快收敛，我觉得从反向传播中可以看出，Relu往前传的导数是1，而Sigmoid是y(1-y)---y是激活后的输出，显然1>y(1-y),说明Relu更新的步子更大，收敛更快。

• 原始的LeNet使用子采样缩小中间数据的大小，即2×2的滤波后，4个输入相加，乘以一个可训练的参数，再加一个可训练的偏置，结果再通过一个Sigmoid，而现在，时代变了，开始用Max池化，说是可以减少参数，这肯定，还可以提取最主要的特征，提高网络的健壮性，健壮性(佩服翻译成这个词的人)--比如，即便输入图像附有一些小的噪声，输出结果也不变，因为它只提取最大。

2、二弟AlexNet,这哥们变种太多，但相对于大哥来说，它的激活函数用ReLU，使用Dropout，还能用GPU，下图就是

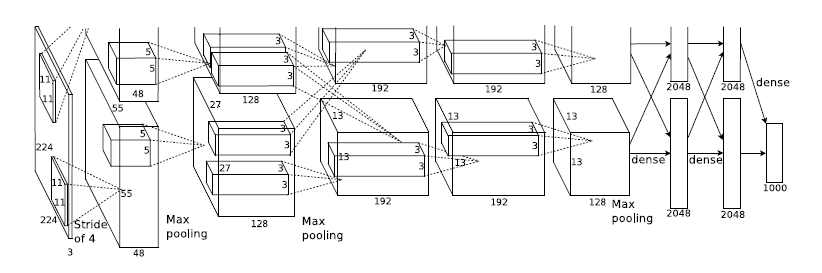
3、三弟VGG，它将有权重的层(卷积层和全连接层)叠加至16层或19层，用3×3的滤波器连续进行，再通过池化层将大小减半，大小可以算算

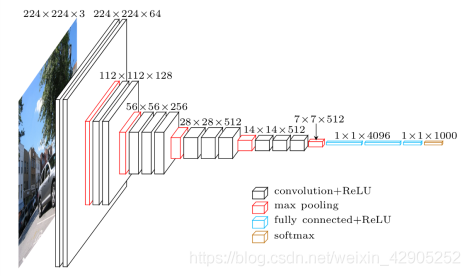
由上图VGG16可知取特征时呈现(2,2,3,3,3)——会出现大小不变很明显加了填充,而VGG19则是(2,2,4,4,4),刚好差了3

4、四弟GoogLeNet,它的特点是不仅纵向上有深度，横向上也有，横向上有宽度被称为Inception(V1，V2，V3，V4)，就是使用多个大小不同的滤波器(和池化)，最后再合并它们的结果，而四弟就是将一个个Inception组合起来，下图就是一个Inception的结构图

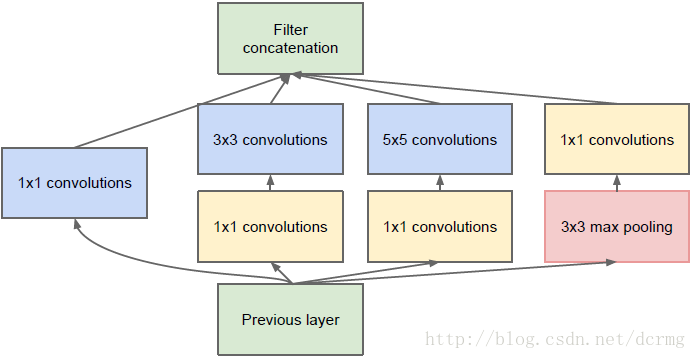
5、五弟ResNet缓解了层太深而使梯度变小的梯度消失问题。为啥层深会出现梯度消失呢，因为随着学习的进行，网络趋于收敛，各参数变动的幅度会越来越小，而当网络很深时，一直往前传的梯度只会越来越小，就很有可能发生梯度消失，学习就进行不下去。为此，五弟在三弟的基础上加了个快捷结构，如下所示

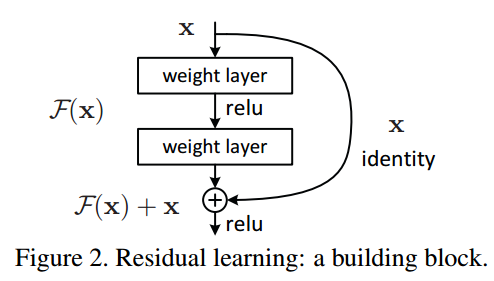
上图的identity就是个快捷结构，它原封不动地传递输入数据，而由加法的反向传播可知，来自上游的梯度会原封不动的传向下游，梯度消失就不易发生。而这整个结构被称Residual Block，即残差块，多个相似的Residual Block串联构成五弟。大致的结构如下图

就写在这吧，后面想起来哪里有错再改改。