训练

7.22
模拟赛：
A：简单题

B：不知道做法是否最简，但是过了。$g_{i,j}$ 表示考虑 t 的 1~i，从 s 的位置 j 开始匹配，最小匹配完的位置。

C：好题。注意到对于长度为 $k$ 的旋律有效，需要所有的 $s_i=s_{i+k}$，而在前面或后面加数不影响两者的对应关系，所以发现 $k$ 出现的时间是连续的，即一旦有一次不行，后面的全都不行。所以我们对这个位置二分，使用字符串哈希可以使时间复杂度降到 $O(nlogn)$。

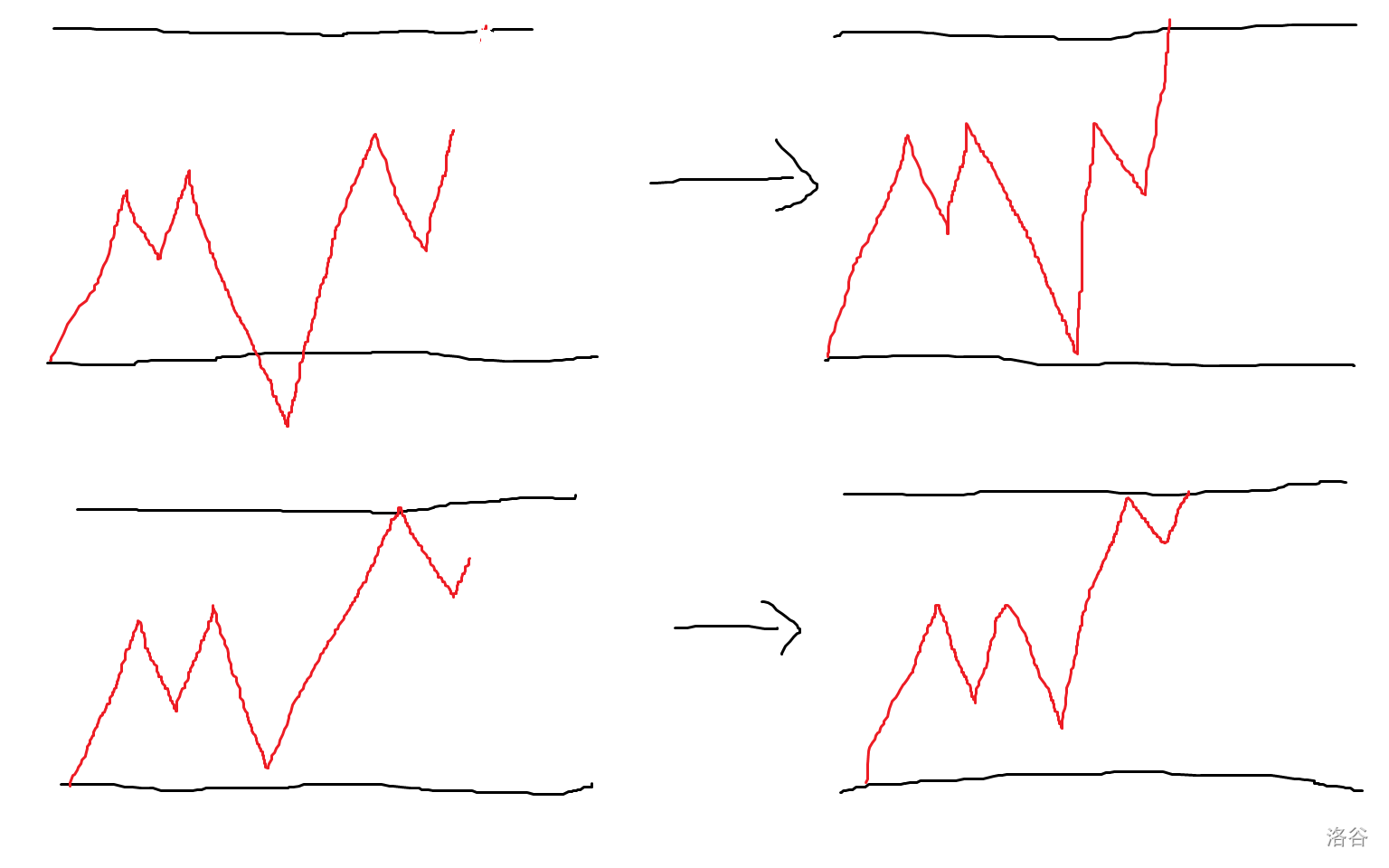
D：妙妙题。把括号、+1-1问题转换为折线是常用的做法（其实只是为了直观）。简单转换发现一个序列可行，当且仅当 $s_{l-1}\leq s_i\leq s_r$. 我们发现，当成立时，最大子段显然等于 $s_r-s_{l-1}$，所以假设结论，应该删去（最大子段-序列和）个-1。
我们构造折线图，上界为最大子段，下界为 $s_l$。接下来考虑如何构造，我们考虑一条折线超过了下界，显然是由于过多 "-1"，那我们删去一些使得他刚好接触下界，此时容易证明即使删去了这些-1，向上平移后最大的点也不会超过上界（如果有的话那么最大子段就不是最大的了，矛盾）。而且删去这些-1显然不会影响最大子段的值。接下来考虑最后可能折线向下，并没有顶上去，那同样我们删去前面的几个-1，使他向上平移到线。
此时我们构造完毕，我们选取了所有的1，删去了尽可能少的-1，是最大的。代码很简单，求区间最大子段即可。

训练：
CF1924B：简单题目，发现显然加的值是等差数列，所以线段树加等差数列和set（维护左边、右边第一个）即可。
P5268：不难想到差分。差分后相乘得到四项，可以轻松用莫队解决。ps：莫队一般解决区间问题，且该区间无法简单用数据结构维护，可以考虑一步一步移动区间端点，时间复杂度一般是 $O(n\sqrt{n})$.

7.23
CF1208D：发现正着考虑并不好做，考虑倒着做。发现 $s_n$ 一定是一段前缀的和，即：$s_i=\frac{k*(k-1)}{2}$. 继续往前推到不难想到线段树二分。
CF1690G：简单题，模拟即可，注意当 $a_k-d\ge min_k$ 时不做更新。
CF1913D：选择一个区间删除等价于每次选择相邻两数删除其中较大值。设 $g_i$ 为保留该数，$f_i$ 为不保留。对于每个 $i$ 考虑前面第一个比他小的数 $j$，如果 $i$ 要删除，则 $j$ 必须要保留，或者 $j$ 删除，让 $j$ 之前一个数来删 $i$，即 $f_i=f_j+g_j$。如果 $i$ 要保留，则 $j$ 不保留，或 j~i 有保留的数。题解
CF2000H：简单题，值域线段树维护即可。注意清空线段树不应全部清空，否则tle，应该将 set 中的数一个个清空。
P4587：现将 $a_i$ 排序，不妨设 $s_i=\sum_{j=1}^i a_j$，如果 $a_{i+1}>s_i+1$，则该值无法表示，而这个方法做单次询问时间 $O(N)$，考虑优化。发现我们其实可以一次性加入大量的数。我们将数分为区间 $[2^1,2^2-1]$，$[2^2,2^3-1]$...$[2^k,2^k-1]$，发现对于如此区间，如果该区间第一个数可以加入，则该区间最后一个数也必然可以加入（因为加入第一个数后区间至少增长一倍），所以单次复杂度变为 $O(log|V|)$，配合可持久化线段树，可以实现双 log 查询。
P7706：类似区间 dp。发现要么全部来自左儿子/右儿子，或 $a_i$/$a_k$ 在左/右儿子，问题转化为维护 $a_i-min(b_j)$. 而该问题又可以同样转化，要么都来自左/右儿子，或左儿子 $a_i$，右儿子区min。维护上述即可。
P6617：不妨设 $nxt_i$ 表示 $i$ 后第一个与 $a_i$ 和为 $w$ 的数，则判断可行性 $min_{i=l}^r nxt_i\leq r$. 由于 $nxt_i>i$，所以可以等价为 $min_{i=l}^n nxt_i\leq r$，所以发现对于所有 $nxt_i$ 想同的数，只有最后一个有用，所以对于每一次修改，只需修改前左侧第一个与 $a_i$ 想同 $a_j$ 的值，自己，修改后左侧第一个与 $a_i$ 想同的 $a_k$，即常数次修改。
或者换一种理解方式，如果有 $x,x,w-x$，其实第一个 $x$ 是没有用的，所以我们只需要考虑所有相邻的情况，用这种方法修改会更简单。

CF813F：线段树分治模版。好文章

7.24
HDU7436：昨日线段树分治简单变形。我们要求 $1$ 能到达 $i$ 点的时间和，则考虑每次到对并查集修改 $tag$，使整条路径到点 $i$ 的和刚好是答案。所以我们将 $u$ 和 $v$ 合并时（$u$ 为父节点），应将 $tag_v=tag_v-tag_u$，而分开始，将 $tag_v$ 变为路径上 $tag$ 总和，赋为答案。
HDU6315：势能线段树简单题。由于对于每个 $i$，要修改 $b_i$ 次才会对答案产生一次影响，而 $b_i$ 是排列，我们对于暴力进行修改（可以维护区间minn），应该是调和级数 $O(nlogn)$。最后时间复杂度为 $O(nlog^2n)$。
CF1638E：并没有写珂朵莉，而是线段树。颜色段均摊，线段树暴力维护，即只有当 $c_l=c_{l+1}=...=c_r$ 时修改当前区间，否则向下递归。时间复杂度证明：每次操作最多增加 $O(2)$ 个颜色段，则若当前需修改 $O(k)$ 个区间，则前面至少有 $O(k)$ 次修改，且修改后区间数减少 $O(k)$ 个。所以总共修改颜色段为 $O(q)$，均摊后为 $O(1)$，时间复杂度为 $O(qlogn)$
CF1763C：思路肯定是将开头变为最小，结尾变成最大，这样可以给整个序列赋值。发现如果对一对 $i,j$ 连续做两次操作，即可将两者均变为 $0$。所以找出最大值，将 $a_1$ 和 $a_2$ 变为 $0$，$a_n$ 和 $a_{n-1}$ 变为 0，即可将这个最大值覆盖所有的 $a$. 考虑所有特殊情况，发现只有 $n=2,3$ 时需特殊考虑。
CF459D：简单题。
CF702F：平衡树简单变形。发现枚举客户不太好做，考虑枚举每一件衣服哪些人能买。我们将平衡树 split 成三棵，分别为 $[0,c),[c,2c),[2c,+)$，发现第一段无改变，第三段减少后相对位置不会变化，只有第二段减少后会与第一段相对位置发生变化，考虑直接暴力合并两个区间。由于第二段每次至少减少一半，所以暴力合并次数为 $log$ 级别。

7.25
模拟赛：
A：简单题。但其实求前缀最大值是可以 $O(N)$ 做的，即如果前缀是正数就加上，否则就不加。

B：简单题。

C：首先注意到我们先上升再下降（显然不会一会儿升一会儿降），所以将路径拆位 $1\rightarrow k$ 和 $n\rightarrow k$。又发现我们肯定是一直上升，且最多走一次平路，然后结束（即下降），因为首先一直边上升且前进是很优的，其次如果出现两次平路，我们完全可以先上升一次，再下降一次。因此一直上升一定是不劣的。设 $f_i$ 为到 $i$ 最小步数，因为我们一直上升，所以 $f_i$ 其实就是高度，所以转移很显然：$f_i=min(f_i,max(a[i],f_j+1))$，dij 可以轻松解决。考虑最后统计答案，先讨论没有平路的情况，那直接 $2\times max(f[i],g[i])$，而如果有平路，我们还要多走一步，枚举每一条边即可。

D：妙妙题，整道题很美妙。注意到如果两个区间是包含关系，那大的区间加入小区间的组中不会影响该组的价值。所以考虑先把所有有包含关系的拿走，只剩下最小的那些。而此时剩下的区间由于没有包含关系，我们发现若它们按 $l$ 排序，则 $r$ 也是有序的！考虑 $f_{i,j}$ 表示当前考虑到 $i$，分成了 $j$ 组，$f_{i,j}=\min f_{k,j-1}+r_{k+1}-l_{i}+1$，可以轻松用单调序列维护在 $O(N^2)$ 解决。而剩下的那些大区间，按从大到小排序，前面的单独成组，剩下的加入对应小区间的组即可。枚举 $j:1\rightarrow k$, 即可。

技巧：C 题发现如果正常做，需要考虑高度和距离，不好操作。则应思考是否有可以去掉的维度，是否有最优策略；D 题的多个区间题，应该考虑有包含关系的非常特殊区间之间是否有关系。

T(n)=T(x)+T(n-x)+O(min(x,n-x))

CF1849E：
7.27
模拟赛：
A：简单恶心题。不难发现只有当两个数没有两个1在同一位时答案为1，否则为2。所以维护前面有多少个和自己1的位置完全不一样的位置，容斥即可。

B：大型分讨题。首先如果有3个或以上长度大于等于 $k$ 的串，则不合法。2个，则必须翻转这两个，判断能否即可。1个，则枚举其他所有段，看是否可以翻转即可。0个，直接结束。

C（CF1550E）：典题。二分是自然地，考虑check。容易想到一个 $O(nk2^k)$ 的dp，即 $f_{i,j}$ 表示以 $i$ 结尾 $j$ 的字母出现状态是否可行（其中j为$2^k$）。但是不难发现当 $f_{i,j}$ 为1时，$f_{i+k,j}$ 一定也为1。而我们 $f$ 的值记录的也很差，不妨考虑交换值与状态，这是一个常用的技巧，可以很好的减少 dp 时间复杂度。即考虑 $f_i$ 表示字母出现状态为i，可以达成该情况的最小位置 $f_i$. 那么这样时间复杂度就降到了 $O(k2^k)$.

D：典题+板题。线段树维护是不难想到的。不难发现对于一个区间进入和出来的时间应该是如下的一个情况（数轴下面那段表示超时失败），而手玩后发现（甚至不用手玩，因为函数合并形状不变是必然的）下一个区间还是这样的。所以考虑维护两个转折的位置 $t_1$ 和 $t_2$，每次简单 push_up 即可。

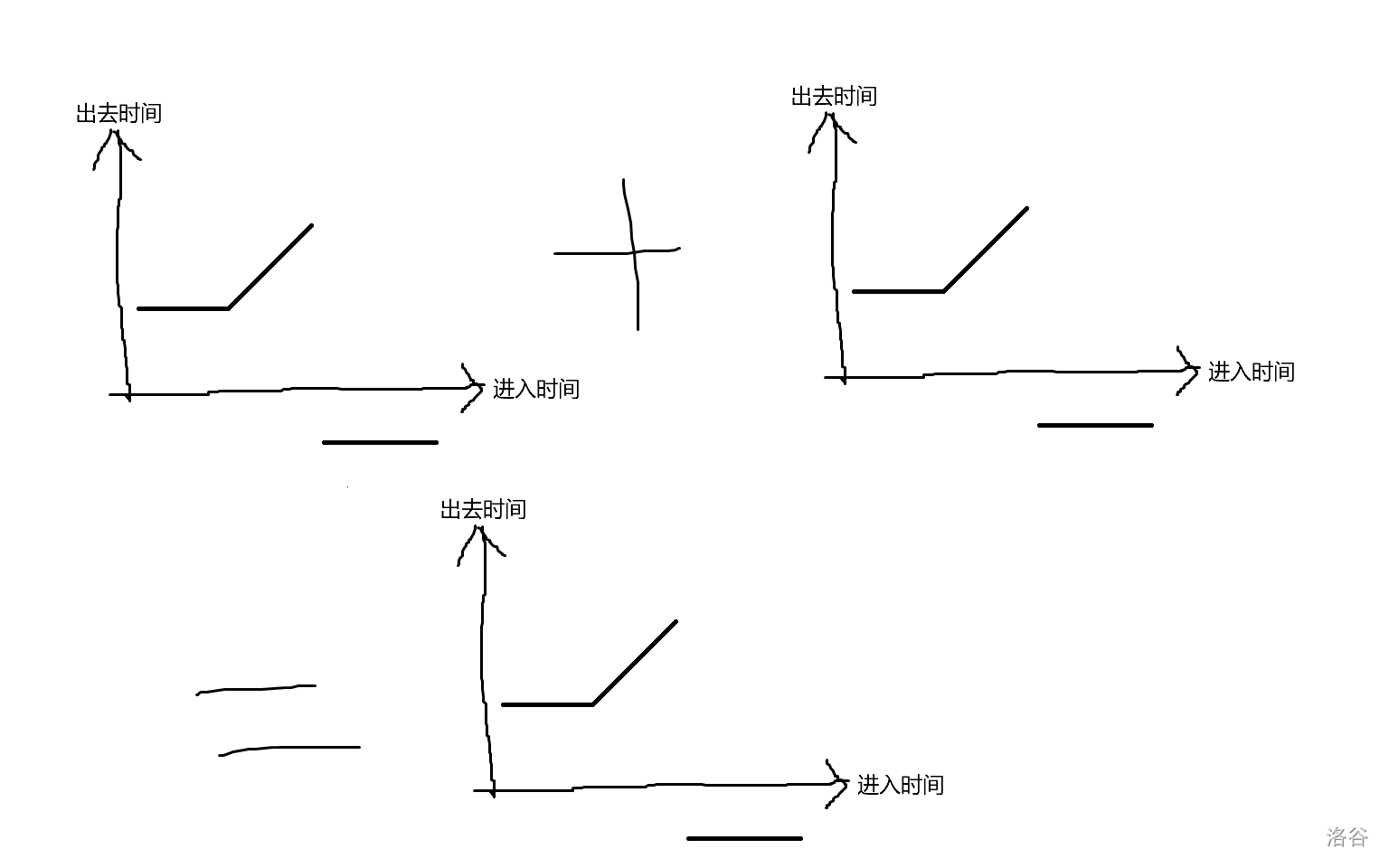
教训：B题应该手动再去思考讨论是否完备。对于 C 题的 $k\leq 17$，显然是状压 $2^k$，去思考不状压是没有前途的。D题在肯定线段树且单点修改时，应该去思考如何设置每个点表示的东西，如何push_up。

7.28
P4696：kmp 妙妙变形题。发现就是让你求有多少个子串和 $p$ 的大小关系是一样的，因为是子串匹配，考虑 kmp。考虑如何判断两个串的大小关系一样，其实就是前面第一个比他小的位置和大的位置相对相同？？？？？？？？？？？？？？？？？

这题还有疑问，为何不能是前面比他小的有几个，大的有几个！！！！

CF1874C：首先遇到概率 dp 题，
CF1458B：简单复杂题。发现如果知道选的杯子的容量和，就比较好做了。所以考虑一个背包，$f_{i,j}$ 表示选了 $i$ 个杯子，容量和为 $j$，这些选了的杯子中已有水量最多是多少。这下最后我们把剩下的除以 $2$，然后相加取 $\max$ 即可。注意做背包一定要倒着做！！！！！

7.29

E - ReTravel

CF1324E：简单题。

CF2000F：简单题，dp+贪心即可。

CF1557D：先离散化，用线段树维护区间极值，然后查询区间极值是自然的想法。但我们若维护题目要求的最小删了多少个，则每轮都要进行一次区间加，这样和区间取min合起来很恶行。于是正难则反，我们求最多保留多少个，那这样我们只需要维护区间max，然后找到后+1即可。
注意：pair<int,int> 的 max/min 并不是每个位置取max/min，而是根据第一/二关键字类似排序后选择，即不会打乱原来 pair 中的东西。

CF780F：dp 好题。像这种两个拼串的应该要想到二进制的拼接，那其实我们只要预处理 $2^i$ 的可行性，就可以像快速幂一样得到最大值。考虑 $f_{i,0/1,u,v}$ 表示从 $u$ 到 $v$ 是否有以 $0/1$ 为开头，长度为 $2^i$ 的路径，转移是容易的，得到结果也是容易的。

QOJ9879(E - ReTravel)：对于走的路线，我们会往上/右走，然后再回退回来，我们发现这个路径一定是类似一个树（有环一定不优）。而对于每个交点，它会向两个方向延伸，然后回来，而左右两个方向会是两个区间的点，这启发我们进行区间类型的dp（$n=500$ 也启发我们进行 $n^3$ 的算法）。那么我们发现对于每个区间，我们的起点应该是 $(\min(x),\min(y))$，然后我们进行简单区间dp即可。

未证明为何从该起点开始！！！！

CF1601D：贪心观察（注意）题。发现以 $\max(s_i,a_i)$ 为第一关键字，$s_i$ 为第二关键字排序即可。

Gym105139D（P10861）：做过。决策单调性简单题。

CF311B：斜率优化简单题。

7.30

模拟赛
A：简单题。

B：高维后缀和（SOS dp）板题，可以稍作复习。

//遍历x的所有子集，O(3^N)，其中N为log x
for(int i=x;i;i=x&(i-1)) 
//高维后缀和，注意转移顺序，但本题求max，即使重复计算也无所谓
for(int i=0;i<20;i++)
	for(int j=0;j<n;j++)
		if(!((i>>j)&1)) chkmx(f[j],f[j^(1<<i)]);

C：注意到，我们先不考虑要怎么选择一次操作的 $l,r$，我们先考虑要在哪些地方断开。发现如果将某个区间断开，我们可以将这个区间加上一个极大值，使这个区间永远和其他区间不一样。所以不难发现一种策略，即贪心的断开区间，能不断就不断，直到必须要断的时候，最后判断一下首尾两个区间是否有重复，然后除以 $2$ 即可。但这个做法是错误的（我也不太知道为什么），因为其实首尾两个区间如果相同是要多一次操作的，所以我们并不能贪心的选择第一个区间。所以我们考虑枚举第一次断开的位置 $l$，使用双指针维护 $r$，使得 $1\sim l$ 和 $r\sim n$ 中无重复元素。再预处理一个数组，记录 $i$ 至少要跳（断）多少次才能到 $n$，并记录最后一个跳（断）的位置。然后开始做，我们发现，如果从 $l+1$ 开始跳的最后一个跳的位置 $<r$，说明这个首位是有重复的，要多跳一次。否则就无所谓。所有结果取 $\min$ 即可。

D：两种做法。
方法一：

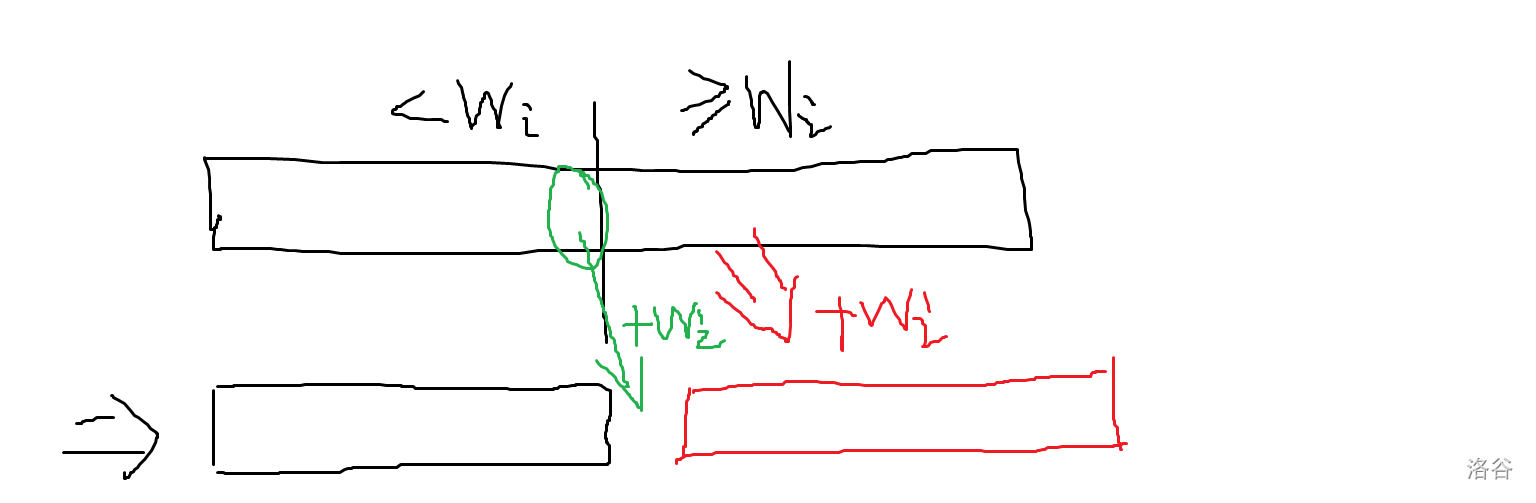
注意到答案一定是递增的（证明不难）。首先正着做 dp 是不可做的，考虑倒着做。$f_{i,j}$ 表示考虑 $i$ 到 $n$ 的所有物品，拿了 $j$ 个出来，的最小初始重量（即若以该重量从 $i$ 开始拿物品可以拿 $j$ 个）。考虑转移，如果 $f_{i+1,j}<w_i$，那么即使多出 $i$ 这个物品我们也拿不了，故 $f_{i,j}=f_{i+1,j}$ ；如果 $f_{i+1,j}\ge w_i$，那么我们就必须拿这个物品，故 $f_{i,j+1}=f_{i+1,j}+w_i$. 而这个 dp 我们可以用平衡树维护。具体的，每次按照 $w_i$ split，对于 $\ge w_i$ 的部分打上 $w_i$ 的 tag标记，然后我们会空缺一个位置，把前面的数拉过来补全即可。

方法二：

显然每次的答案是一堆货物相加的总和，那我们考虑对于每次 $i\rightarrow i-1$，会减少哪些货物。我们不妨构造一个序列，倒序插入，每次 $a_i$ 插入的位置是前缀和小于它的最后一个位置。
以样例 10 8 3 30 5 10 举例：$[10]\rightarrow[5,10]\rightarrow[5,10,30]\rightarrow[3,5,10,30]\rightarrow[3,8,5,10,30]\rightarrow[3,10,8,5,10,30]$.
然后就发现 $ans_i-ans_{i-1}=b_i$. 考虑为何。
如果某个数大于一个后缀中的某些数，则如果想选择这一个后缀中的数，则必须要先把这个数选上，而把这个数删除，后面就能正常选择了。（感觉证明很差）
考虑维护，首先插入的话很难做，不妨直接用线段树维护自己和后缀的差，每次在线段树上找第一个大于 $0$ 的位置即可，然后将改点设为无穷小。

CF1096D：简单题。
P10156：发现如果每次枚举哪两个人同时踢走，会是 $O(N^3)$ 的。考虑我们能否简单的从 $i-1$ 进行转移，这时我们发现可以拆贡献，对于奇数位置，我们加上负的贡献；偶数位置，加上正的贡献。最后处理一下团体与团体之间的关系即可。
CF1336C：好题。发现可以看做一个区间在前或后增加一个字符变成一个新区间，考虑区间 dp。所以考虑 $f_{i,j}$ 表示 $s_1$ 到 $s_{j-i+1}$ 与 $t_i$ 到 $t_j$ 匹配。这样每次只用考虑把这个字符加在前面还是后面。至于前缀，把 $t$ 后面加上通配符即可。
Gym104128B：好题。如果没有修改操作，dp 加上单调队列是容易的。发现一个位置的答案可以拆成两部分，即从 $0$ 到它，和从它到 $n+1$，不妨记录前者为 $f_i$ 后者为 $g_i$，可以使用单调队列预处理。考虑如何修改，若对 $i$ 修改，$i-1$ 之前的答案并不受影响，同理我们的后缀 $g$ 也是不受影响的，又发现其实对于一个点 $j$，$[j,j+k)$ 区间内必有一个点转移出去，所以我们每次修改只需要暴力更新 $O(k)$ 个区间，然后用更新的 $f(i)$ 加上后缀 $g(i)$ 求出该点的值。总时间复杂度：$O(n+qk)$。
>思路：发现每次修改会导致后面所用东西重算，这个我们无法承受，但是我们发现 $[j,j+k)$ 必有一个点转移出去，所以我们就考虑把答案拆成区间点贡献 $\max$，点贡献又可以拆成前后两部分，而暴力维护 $O(k)$ 个位置我们是可以接受的。

7.31

CF1436C：简单题。

P9306：简单题。

CF571A：正难则反。发现我们并不好同时维护 $a+b>c,a+c>b,b+c>a$ 这几个条件，则考虑找出不符合要求的。首先总共情况有 $\binom{l+2}{2}$ 种

关于 $O(N)$ 递推求逆元的证明：

求 $i$ 的逆元。设 $p=[\frac{M}{i}],q=M-pi$。其中 $M$ 为模数
则有：$$ip+q\equiv 0 \pmod{M} $$
两边同除 $iq$：$$pq^{-1}+i\equiv 0\pmod{M}$$
移项：$$i^{-1}\equiv -pq^{-1}\pmod{M}$$
综上，$inv[i]=-(M/i)inv[M\%i]=(M-M/i)inv[M\%i]$。

8.2
模拟赛
A：首先显然无单调性，无法二分。发现好像根本无法优化，因为只能暴力枚举每个可能值，然后跑一次暴力模拟选取器材。所以考虑证明时间复杂度，发现体积 $W$ 的下限，显然是 $\left \lceil \frac{sum}{k}\right \rceil$。再思考上界，发现下界的问题是有时候会空出导致浪费，所以我们不妨加上一个 $maxn$（$v_i$ 中的最大值）。这个时候我们无论如何都可以多拿一个进来，显然是可以满足要求的。其中模拟过程可以使用 set 优化至 $O(n\log_{}{n})$。所以时间复杂度为 $O(n\log_{}{n}|V|)$。

B：确实是简单题。先把所有 ? 设为 $0$。我们考虑连续 ? 串左边和右边的数字，如果是 0...1 或 1...0 我们改变 $0$ 变成 $1$ 是有办法使答案不增加的，记为类型1；如果是 1...1，则在我们改变 $len$ 次后可以使答案减少 $2$，记为类型2；如果是 0...0，则在我们改变中间一次后就会使答案增加 $2$，记为类型3。那贪心策略其实比较显然，先做类型2，按 $len$ 从小到大排序；再做类型1，顺序无所谓；最后做类型3，按 $len$ 从大到小排序。

C（I - XOR Reachable）：发现光是想统计答案已经会爆时间，似乎只有在维护并查集时同步更新答案才能够维护。多次询问，每次有一些边是符合的，求方案数，甚至还有并查集，很明显的线段树分治思想。所以考虑把边权建 trie，把询问挂在 trie 的叶子上，然后遍历整个 trie 统计答案即可。
具体地，我们考虑 $k$ 的第 $i$ 位：如果为 $0$，那么当 $d$ 为 $1$ 时，我们要往 $1$ 走（这要异或起来才行），$d$ 为 $0$，就往 $0$ 走；如果为 $1$，那么当 $d$ 为 $0$ 时，$0$ 那边所有数都是可行的，应该全部加入并查集（因为异或这一位已经小于了，后面无所谓），然后往 $1$ 那边走，而为了方便操作，我们应该在加入边操作时如果 $k$ 这一位为 $1$ 时交换左右子树（这样才能左边往左边走），$d$ 为 $1$ 同理。
考虑证明时间复杂度，首先加边和加询问是单次是 $O(\log_{}{n})$ 的，而做查询时正常 $k$ 为 $0$ 时走复杂度显然无问题，考虑是 $1$ 时因为一次要加一个子树的边，然后删掉。考虑一个点被加入次数，只有可能在他的所有直系祖先上，而这样的祖先只有 $O(\log_{}{n})$ 个。总时间：加边，$O(n\log_{}{n})$；遍历整个 trie 树 $O(n\log_{}{n})$，加边操作总共最多有 $O(n\log_{}{n})$ 次，加上并查集无法压缩路径考虑启发式合并的 $O(\log_{}{n})$，总时间复杂度为 $O(n\log^2_{}{n})$。

应该是的，时间复杂度没证错吧？？？？？

D：Editorial - UTPC 2024

8.4

模拟赛
A：对每种宝石单独考虑，显然它的情况数先要乘上其他随便选的方案，即：$2^{sum-c_i}$。然后考虑同种宝石，发现是一个：

\[C_{c_i}^{1}\times v_i+C_{c_i}^{2}\times v_i^2+...+C_{c_i}^{c_i}\times v_i^{c_i} \]

这是显然是一个二项式定理的展开形式（但是少了第一项），原式应为：

\[(v_i+1)^{c_i} \]

算出这个式子后减去一个 $1$ 即可。

B：

C：看出是 dp 并不难，但是问题是如何设置状态和转移。其实我们发现，把所有 $B$ 集合中最外面的连起来，应该是类似一个阶梯状的东西，其中这个东西的右下角必须全部是 $B$ 集合的。所以我们考虑 dp 这个外轮廓。我们先钦定所有数字在 $A$ 集合，则每个数代价变为 $b_i-a_i$，我们需要求代价最大值。设 $f_i$ 表示点 $i$ 放入 $B$ 集合代价最大值。发现 $f_i$ 只有可能从 $y$ 小于等于它的位置转移，否则就不是外轮廓；在考虑这个点如果不在外轮廓上，会对哪些点做出贡献，发现 $y$ 比它大的都会做出贡献，然后这个 dp 显然可以用线段树维护。
具体地，

补图！！！

D：不知道自己做法是否正确，是否是数据过水导致AC。这题100%正确做法应该是删边最短路。
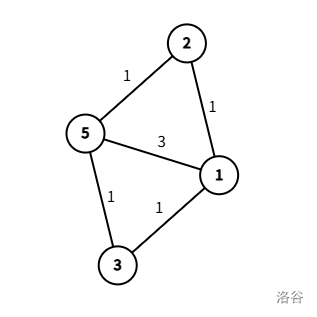
自己做法：首先一条边 +2 和删去这条边无区别。发现删去的边一定在所有从 $1$ 到 $n$ 最短路的交集里，我们现建出最短路径生成树，而答案边一定在里面，我们不会算少。然后我们发现，次短路应该只会有一条路不在最短路径树里，否则肯定会有更优的路径（证明不难）。所以我们考虑从 $n$ 一直往 $fa$ 跳跳到 $1$，枚举每一条可以删去的边 $x\rightarrow fa_x$，此时树被分成了两个集合，由于两个集合一个只增加，一个只减少，我们可以快速的维护是否出现了从上面集合走一条非树边到下面集合且比最短路恰好多 $1$ 的方案数。但是这样我们会计算多的答案，思考：从 $1$ 到 $n$ 不仅只有一条最短路，如果虽然在我们删边后确实会有比答案恰好多 $1$ 的路径，但有可能还有第 $2$ 条从 $1$ 到 $n$ 不经过这条边的最短路。所以我们考虑把最短路径图建出来，找出里面所有的割边（桥），然后扔到一个 map 里。每次找到答案去 map 里找这是不是割边，如果是才计入答案。

原方法hack如下：如图，我们建出的最短路径树可能是 $1\rightarrow 2\rightarrow 5$，我们删掉 $1\rightarrow 2$ 的边也确实会有一条比最短路径大 $1$ 的路径，但是显然 $1\rightarrow 3\rightarrow 5$ 是另一条最短路径。

posted @ 2025-09-06 12:23 ziyistudy 阅读(5) 评论(0) 收藏举报

刷新页面返回顶部

ziyistudy

训练

这题还有疑问，为何不能是前面比他小的有几个，大的有几个！！！！

未证明为何从该起点开始！！！！

应该是的，时间复杂度没证错吧？？？？？

补图！！！

公告