算法基础之动态规划法
本文将详细介绍动态规划法的基本原理和适用条件，并通过经典例题辅助读者理解动态规划法的思想、掌握动态规划法的使用。本文给出的例题包括：多段图问题、矩阵连乘问题、最长公共子序列问题。
本文将详细介绍动态规划法的基本原理和适用条件，并通过经典例题辅助读者理解动态规划法的思想、掌握动态规划法的使用。本文给出的例题包括：多段图问题、矩阵连乘问题、最长公共子序列问题。
算法原理
动态规划是一种解决多阶段决策问题的优化方法，把多阶段过程转化为一系列单阶段问题，利用各个阶段之间的关系逐个求解。与分治法类似，动态规划法也是将待求解的问题分解为若干个子问题（阶段），但分治法中各子问题相互独立，而动态规划法适用于子问题重叠的情况，也即各子问题包含公共的子子问题。与贪心法类似，动态规划法可将一个问题的解决方案视为一系列决策的结果，但动态规划可以处理不满足贪心准则的问题。
动态规划法所能解决的问题一般需要满足以下性质：
- 最优性原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优性原理。
- 无后效性：某阶段的状态一旦确定，就不受这个状态以后决策的影响。也即，某状态以后的过程不会影响以前的状态，只与当前的状态有关。
- 有重叠子问题：子问题之间是不独立的，一个子问题在下一个阶段决策中可能被多次使用。该性质是不是动态规划法适用的必要性质，但若无该性质，则动态规划法与其它算法相比不具备优势。
动态规划法的步骤：
- 分析最优解的性质，并刻画其结构特征；
- 递归定义最优解；
- 以自底向上或自顶向下的记忆化方式计算出最优值；
- 根据计算最优值得到的信息构造问题的最优解。
多段图问题
题目描述
设图 \(G=(V,E)\) 是一个带权有向图，图中的顶点被划分成 \(k\) 个互不相交的子集 \(V_i\)，\((2≤k≤n,1≤i≤k)\)，使得 \(E\) 中任意一条边 \(<u,v>\) 必有 \(u∈V_i，v∈V_j\)，\((1≤i<k,1<j≤k)\)，则称图 \(G\) 为多段图，称 \(s∈V_1\) 为源点，\(t∈V_k\) 为汇点，\(V_1\) 和 \(V_k\) 分别只有一个顶点。多段图的最短路径问题即为求从源点到汇点的最小代价路径（顶点编号从 \(0\) 开始，默认顶点 \(0\) 为源点，顶点 \(|V|-1\) 为汇点）。
输入输出
输入：先输入顶点个数 \(V\) 和边数 \(E\)，接着 \(E\) 行输入 \(E\) 条边及边的权值 \((u,v,w)\)。
输出：第一行输出最短路径（用→连接），第二行输出最短路径的长度。
向后处理
以下图所示带权有向图为例（记为 \(G\)），解释如何通过“向后处理”求解最短路径以及最短路径的长度。
\(n\) 个顶点依次编号为 \(0,1,...,n-1\)，设 \(d[i]\) = 源点 \(s\) 到顶点 \(i\) 的最短路径的长度，则有 \(d[j]=min\{d[i]|∃<i,j>∈E\}\)。具体做法：
- 将 \(d[0..n-1]\) 置为 \(INF\)，设当前段所有点的集合为 \(Vcur\)，下一段所有点的集合为 \(Vnext\)，源点 \(s\) 所在段的顶点的集合为 \(Vs\)，汇点t所在段的顶点的集合为 \(Vt\)，\(Vcur\) 初始置为 \(Vs\)，\(Vnext\) 由 \(Vcur\) 和边相关信息推出；
- 根据 \(Vcur\) 中的每一个顶点 \(i\) 尝试去更新 \(Vnext\) 中的每一个顶点j对应的 \(d[j]\)，即，若 \(d[j]>d[i]+cost[i][j]\)，则 \(d[j]=d[i]+cost[i][j]\)，并记录j的前驱 \(pre[j]\) 为 \(i\)，否则，不作处理；
- \(Vcur=Vnext\)，\(Vnext\) 通过 \(Vcur\) 和边相关信息推出；
- 若 \(Vcur!=Vt\)，则重复步骤 \(2\) 和 \(3\)，否则，程序结束，\(d[t]\) 即为源点 \(s\) 到汇点 \(t\) 的最短路径的长度，\(pre\) 记录了最短路径上每个顶点的前驱。
// 准备工作
#define INF (INT_MAX/2-1)
typedef vector<int> vi;
int V, E; // 点数 边数
struct edge { int to, w; }; // 边
vector<vector<edge>> es; // es[i] 以i为起始点的边的集合
vi d; // 各点到源点s的最短距离，初始化为INF
vi pre; // pre[i] 最短路径上顶点i的前驱，初始化为-1
int main() {
// 输入
cin >> V >> E;
es.resize(V), d.resize(V, INF), pre.resize(V, -1);
for (int i = 0, u, v, w; i < E; ++i) {
cin >> u >> v >> w;
es[u].push_back({v, w});
}
// 求解
mulSegGraph(0);
vi path = getPath(V-1);
// 输出
printf("%d", path[0]);
for (int i = 1; i < path.size(); ++i)cout << "->" << path[i];
printf("\n%d", d[t]);
}
/**
* 求多段图问题
* @param s 源点
*/
void mulSegGraph(int s) {
queue<int> seg; // 段
seg.push(s), d[s] = 0; // 源点入队列，起点到起点的距离设为0
while (!seg.empty()) {
int i = seg.front();
seg.pop();
// 更新所有以i为起始点的边的终点到起点s的最短距离
for (auto &e: es[i]) {
if (d[e.to] > d[i] + e.w) {
d[e.to] = d[i] + e.w;
pre[e.to] = i;
seg.push(e.to);
}
}
}
}
/**
* 求源点s到汇点t的最短路径
* @param t 汇点
* @return 最短路径
*/
vi getPath(int t) {
vector<int> path;
for (; t != -1; t = pre[t])path.push_back(t);
reverse(path.begin(), path.end());
return path;
}
时间复杂度：\(O(E+K)\)，其中，\(E\) 表示多段图的边数，\(K\) 表示多段图的段数。
空间复杂度：\(O(V+E)\)，其中，\(V\) 为多段图的顶点数。
向前处理
向后处理即从源点 \(s\) 出发，向汇点 \(t\) 迈进，向前处理则是从汇点 \(t\) 倒推回源点 \(s\)，处理方法与向后处理类似。\(n\) 个顶点依次编号为 \(0,1,...n-1\)，设 \(d[i]\) = 顶点 \(i\) 到汇点 \(t\) 的最短路径的长度，则有 \(d[i]=min\{d[j]|∃<i,j>∈E\}\)。具体做法：
- 将 \(d[0..n-1]\) 置为 \(INF\)，设当前段所有点的集合为 \(Vcur\)，上一段所有点的集合为 \(Vpre\)，源点 \(s\) 所在段的顶点的集合为 \(Vs\)，汇点 \(t\) 所在段的顶点的集合为 \(Vt\)，\(Vcur\) 初始置为 \(Vt\)，\(Vpre\) 由 \(Vcur\) 和边相关信息推出；
- 根据 \(Vcur\) 中的每一个顶点 \(j\) 尝试去更新 \(Vpre\) 中的每一个顶点 \(i\) 对应的 \(d[i]\)，即，若 \(d[i] > d[j] + cost[i][j]\)，则 \(d[i] = d[j] + cost[i][j]\)，并记录 \(i\) 的后继 \(nex[i]\) 为 \(j\)，否则，不作处理；
- \(Vcur = Vpre\)，\(Vpre\) 通过 \(Vcur\) 和边相关信息推出；
- 若 \(Vcur != Vs\)，则重复步骤 \(2\) 和 \(3\)，否则，程序结束，\(d[s]\) 即为源点 \(s\) 到汇点 \(t\) 的最短路径的长度，\(nex\) 记录了最短路径上每个顶点的后继。
// 准备工作
#define INF (INT_MAX/2-1)
typedef vector<int> vi;
int V, E; // 点数 边数
struct edge { int from, w; }; // 边
vector<vector<edge>> es; // es[i] 以i为终点的边的集合
vi d; // 各点到汇点t的最短距离，初始化为INF
vi nex; // nex[i] 最短路径上顶点i的后继，初始化为-1
int main() {
// 输入
cin >> V >> E;
es.resize(V), d.resize(V, INF), nex.resize(V, -1);
for (int i = 0, u, v, w; i < E; ++i) {
cin >> u >> v >> w;
es[v].push_back({u, w});
}
// 求解
mulSegGraph(V-1);
vi path = getPath(0);
// 输出
cout << path[0];
for (int i = 1; i < path.size(); ++i)cout << "->" << path[i];
cout << '\n' << d[s];
}
/**
* 求多段图问题
* @param t 汇点
*/
void mulSegGraph(int t) {
queue<int> seg; // 段
seg.push(t), d[t] = 0; // 汇点t入队列，汇点t到汇点t的距离设为0
while (!seg.empty()) {
int i = seg.front();
seg.pop();
// 更新所有以i为终点的边的起始点到汇点t的最短距离
for (auto &e: es[i]) {
if (d[e.from] > d[i] + e.w) {
d[e.from] = d[i] + e.w;
nex[e.from] = i;
seg.push(e.from);
}
}
}
}
/**
* 求源点s到汇点t的最短路径
* @param s 源点
* @return 最短路径
*/
vi getPath(int s) {
vi path;
for (; s != -1; s = nex[s])path.push_back(s);
return path;
}
时间复杂度：\(O(E+K)\)，其中，\(E\) 表示多段图的边数，\(K\) 表示多段图的段数。
空间复杂度：\(O(V+E)\)，其中，\(V\) 为多段图的顶点数。
优化处理
观察向前处理和向后处理两种方案的输出结果发现，对于同一个多段图，二者给出的最短路径并不相同，但最短路径的长度是相同的。这是因为，当前多段图存在多条最短路径，而两个方案中存储最短路径的数组均为一维数组，只能记录一条最短路径。
为此，以向后处理为例，修改记录最短路径的数组 \(pre\) 为二维数组，\(pre[i]\) 用于记录每一条最短路径上节点 \(i\) 的前驱，即 \(pre[i]\) 为节点 \(i\) 的前驱的集合。在向后处理的的基础上做如下修改（与向前处理类似）。
...
vector<set<int>> pre; // pre[i] 最短路径上顶点i的前驱的集合
...
int main() {
...
pre.resize(V), pre[0].insert(-1);
...
// 读取最短路径
vector<vi> paths;
vi path;
getPaths(t, paths, path);
// 输出
for (const auto &ph: paths) {
cout << ph[0];
for (int i = 1; i < ph.size(); ++i)cout << "->" << ph[i];
}
...
}
void mulSegGraph(int s) {
...
while (!seg.empty()) {
...
for (auto &e: es[i]) {
if (d[e.to] >= d[i] + e.w) {
// 记录多条路径
if (d[e.to] > d[i] + e.w) {
// 找到到e.to更短的路径则清除e.to原来记录的前驱
pre[e.to].clear();
pre[e.to].insert(i);
d[e.to] = d[i] + e.w;
}
// 找到与目前到e.to的最短路径长度相同的路径则记录
else pre[e.to].insert(i);
seg.push(e.to);
}
}
}
}
/**
* 求源点s到汇点t的所有最短路径
* @param t 汇点
* @param paths 所有路径
* @param path 已搜索到的路径
*/
void getPaths(int t, vector<vi> &paths, vi path) {
if (t == -1) { // 当前最短路径搜索完毕
reverse(path.begin(), path.end());
paths.push_back(path);
return;
} else path.push_back(t);
for (auto &p: pre[t])getPaths(p, paths, path);
}
时间复杂度：\(O(E+MK)\)，其中，\(E\) 表示多段图的边数，\(M\) 表示最短路径的数目，\(K\) 表示多段图的段数。
空间复杂度：\(O(V+E)\)，其中，\(V\) 为多段图的顶点数。
矩阵连乘问题
题目描述
给定 \(n\) 个矩阵 \(A_0,A_1,…,A_{n-1}\)，其中 \(A_i\) 的维数为 \(p_i × p_{i+1}\)，并且 \(A_i\) 与 \(A_{i+1}\) 是可乘的。考察这 \(n\) 个矩阵的连乘积 \(A_0 × A_1 ×…× A_{n-1}\)，由于矩阵乘法满足结合律，所以计算矩阵的连乘可有许多不同的计算次序。矩阵连乘问题是确定计算矩阵连乘积的计算次序，使得按照这一次序计算矩阵连乘积，需要的“数乘”次数最少。
输入输出
输入：第一行输入 \(n\) 的值，第二行输入 \(n\) 个矩阵的维数 \(p_i\)。
输出：最少数乘次数以及对应的计算次序。
基础实现
设 \(m[i][j]=A_i...A_j\) 的最小数乘次数 \((0≤i≤j≤n-1)\)，\(p[i]\) = 矩阵 \(A_i\) 的行数，\(p[i+1]\) = 矩阵 \(A_i\) 的列数 = 矩阵 \(A_{i+1}\) 的行数 \((0≤i≤n-1)\)，则有 \(m[i][j] = min\{m[i][k] + m[k+1][j] + p[i] × p[k+1] × p[j+1]\ |\ i<k<j\}\)，当 \(i=j\) 时，有 \(m[i][j]=0\)，也即 \(m[i][i]=0\)。为了后续输出对应的计算次序，增加数组 \(b\) 用于记录划分点，\(b[i][j]=A_i...A_j\) 的划分点，划分点属于左侧。
typedef vector<int> vi;
int N; // 矩阵数
vi p; // p[i] 矩阵Ai的行数，同时也是举证Ai+1的列数
vector<vi> m; // m[i][j] Ai...Aj的最小数乘次数
vector<vi> b; // b[i][j] Ai...Aj的划分点，划分点属于左侧
int main() {
// 输入
cin >> N;
p.resize(N + 1, 0), m.resize(N, vi(N, 0)), b.resize(N, vi(N, -1));
for (int i = 0; i <= N; ++i)cin >> p[i];
// 求解
minNumMul();
// 输出
cout << m[0][N - 1] << endl;
bracket(0, N - 1);
}
/**
* 计算A0A1...An-1的最少数乘次数
*/
void minNumMul() {
int i, j, k;
// 求k个矩阵相乘时的最少数乘次数
for (k = 2; k <= N; k++)
// 求每个长度为k子序列(i,j)的子序列的划分点（划分点属于左侧）
for (i = 0; i < N - k + 1; i++) {
j = i + k - 1;
// 以i为划分点赋初值，省略+m[i][i]，因为m[i][i]=0
m[i][j] = m[i + 1][j] + p[i] * p[i + 1] * p[j + 1];
b[i][j] = i;
// 尝试每个可能的划分
for (int r = i + 1, t; r < j; r++) {
t = m[i][r] + m[r + 1][j] + p[i] * p[r + 1] * p[j + 1];
if (t < m[i][j]) {
m[i][j] = t; // 记录数乘数
b[i][j] = r; // 记录划分点
}
}
}
}
/**
* 显示Ai...Aj数乘次数最少时对应的计算次序
*/
void bracket(int i, int j) {
cout << "(";
if(i == b[i][j])printf("A%d", i); // 划分点b[i][j]左侧没有划分点
else bracket(i, b[i][j]);
if (b[i][j] + 1 == j) // 划分点b[i][j]右侧没有划分点
for (int k = b[i][j] + 1; k <= j; ++k) printf("A%d", k);
else bracket(b[i][j] + 1, j);
cout << ")";
}
时间复杂度：\(O(n^3)\)。
空间复杂度：\(O(n^2)\)。
优化处理
观察 \(minNumMul()\) 函数发现，二维数组 \(m\) 只利用了下标 \(i≤j\) 的空间，二维数组 \(b\) 只利用了下标 \(i<j\) 的空间，而且二者大小均为 \(N×N\) 。因此，为了节约空间，可以将两个二维数组合并，具体做法就是用 \(m[j\)][i] 直接替换掉原来的 \(b[i][j]\)，其中 \(i<j\)。在基础实现的基础上做如下修改：
void minNumMul() {
...
for (k = 2; k <= N; k++)
for (i = 0; i < N - k + 1; i++) {
...
// b[i][j] = i;
m[j][i] = i;
for (int r = i + 1, t; r < j; r++) {
...
if (t < m[i][j]) {
...
// b[i][j] = r;
m[j][i] = r;
}
}
}
}
void bracket(int i, int j) {
cout << "(";
if (i == m[j][i])printf("A%d", i); // 划分点b[i][j]左侧没有划分点
else bracket(i, m[j][i]);
if (m[j][i] + 1 == j) // 划分点b[i][j]右侧没有划分点
for (int k = m[j][i] + 1; k <= j; ++k) printf("A%d", k);
else bracket(m[j][i] + 1, j);
cout << ")";
}
时间复杂度：\(O(n^3)\)。
空间复杂度：\(O(n^2)\)。
最长公共子序列问题
题目描述
给定两个序列 \(X=\{x_1,x_2,…,x_m\}\) 和 \(Y=\{y_1,y_2,…,y_n\}\)，找出 \(X\) 和 \(Y\) 的最长公共子序列。
输入输出
输入：第一行输入序列 \(X\)，第二行输入序列 \(Y\)。
输出：\(X\) 和 \(Y\) 的最长公共子序列和最长公共子序列的长度
基础实现
设 \(L[i][j]\) 为 \(x_1...x_i\) 与 \(y_1...y_j\) 的最长公共子序列（设为 \(Z\) ）的长度，则有
- ① \(i=0\) 或 \(j=0\) 时，\(l[i][j]=0\)；
- ② 当 \(Z\) 末位不为 \(x_i\) 不为 \(y_j\) 时，\(L[i][j]= L[i-1][j-1]\)；
- ③ 当 \(Z\) 末位不为 \(x_i\)为 \(y_j\) 时，\(L[i][j]= L[i-1][j]\)；
- ④ 当 \(Z\) 末位为 \(x_i\) 不为 \(y_j\) 时，\(L[i][j]= L[i][j-1]\)；
- ⑤ 当 \(Z\) 末位为 \(x_i\) 且为 \(y_j\) 时（此时 \(x_i\) 与 \(y_j\) 必相等），\(L[i][j]= L[i-1][j-1]+1\)。
综上，若 \(x_i=y_j\)，\(L[i][j]= L[i-1][j-1]+1\)，否则 \(L[i][j]=max(L[i-1][j-1], L[i-1][j], L[i][j-1])\)。
需要注意，③中 \(L[i-1][j]\) 实际表示 \(Z\) 末位不为 \(x_i\) 的情况，比②中前提表示范围要大，但包含了③中前提表示范围，④和⑤中也是类似。虽然如此，但并不影响结果的正确性。①到⑤的前提表示范围可以覆盖所有情况，③④⑤实际表示范围均包含了各自前提表示范围，只不过各自均考虑了一些前提以外的情况，这些情况仍在整体待考虑的范围之内，由于求“最长”，即使重复考虑了某些情况，也并不影响最值。
以字符串 \(abad\) 和 \(baade\) 为例，构造二维数组 \(L\) 如下图所示。
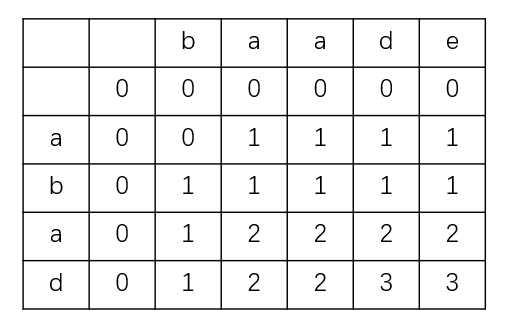
应用上述规则，通过对二维数组 \(L\) 反向搜索，便可以得到最长公共子序列。为了在反向搜索时更加方便地直到 \(L[i][j]\) 究竟来自 \(L[i-1][j]\)、\(L[i][j-1]\)、\(L[i-1][j-1]\) 中的哪一个，可以增设数组 \(W[i][j]\)，在构造二维数组L的同时对 \(L[i][j]\) 来自哪里进行记录。
// L[i][j]: x1x2...xi与y1y2...yj的最长公共子序列的长度
vector<vector<int>> L;
// W[i][j]: L[i][j]的值是通过l[i-1][j]、L[i][j-1]、L[i-1][j-1]中的哪一个得到的
// 用于还原最长公共子序列
vector<vector<int>> W;
// W[i][j]的三个值，分别对应l[i-1][j-1]、L[i-1][j]、L[i][j-1]
int LU = 1, LEFT = 2, UP = 3;
string X, Y; // 字符串
int main() {
// 输入
cin >> X >> Y;
int m = X.length(), n = Y.length();
L.resize(m + 1, vector<int>(n + 1, 0));
W.resize(m + 1, vector<int>(n + 1, 0));
// 求解
lonComSub();
string s = sub();
// 输出
cout << s << '\n' << L[m][n];
}
/**
* 求最长公共子序列即其长度，也即填充l和w
*/
void lonComSub() {
int i, j;
for (i = 0; i < X.length(); ++i) {
for (j = 0; j < Y.length(); ++j) {
if (X[i] == Y[j]) {
L[i + 1][j + 1] = L[i][j] + 1;
W[i + 1][j + 1] = LU; // (i,j)是左上方来的
} else if (L[i + 1][j] > L[i][j + 1]) {
L[i + 1][j + 1] = L[i + 1][j];
W[i + 1][j + 1] = LEFT; // (i,j)是从左边来的
} else {
L[i + 1][j + 1] = L[i][j + 1];
W[i + 1][j + 1] = UP; // (i,j)是从上边来的
}
}
}
}
/**
* 以字符串的形式返回最长公共子序列
*/
string sub() {
string s;
int i = X.length(), j = Y.length();
while (i > 0 && j > 0) {
if (W[i][j] == LU) { // 从左上来的
s = X[i - 1] + s;
i--, j--;
} else if (W[i][j] == LEFT) j--; // 从左边来的
else i--; // 从上面来的
}
return s;
}
时间复杂度：\(O(mn)\)。
空间复杂度：\(O(mn)\)。
优化处理
观察基础实现的测试结果不难发现，当 \(X\) 和 \(Y\) 存在多个最长公共子序列时，程序只输出了其中一个，为此，需要修改获取最长公共子序列的函数，即 \(sub()\) 函数。在基础实现的基础上做如下修改：
int main() {
// 初始化
cin >> X >> Y;
int m = X.length(), n = Y.length();
L.resize(m + 1, vector<int>(n + 1, 0));
W.resize(m + 1, vector<int>(n + 1, 0));
// 求解
lonComSub();
vector<string> ss;
string s;
sub(m, n, ss, s);
// 输出
for (auto &it: ss)cout << it << endl;
cout << L[m][n];
}
/**
* 获取最长公共子序列
* @param i,j 坐标
* @param ss 所有公共子序列
* @param s 目前已搜索到的最长公共子序列
*/
void sub(int i, int j, vector<string> &ss, string s) {
if (i < 1 || j < 1) { // 找到一条路径
ss.push_back(s);
return;
}
if (X[i - 1] == Y[j - 1]) // 左上来的
sub(i - 1, j - 1, ss, X[i - 1] + s);
else if (L[i][j - 1] > L[i - 1][j]) // 左边来的
sub(i, j - 1, ss, s);
else if (L[i][j - 1] < L[i - 1][j]) // 上面来的
sub(i - 1, j, ss, s);
else sub(i, j - 1, ss, s), sub(i - 1, j, ss, s); // 左和上均可能
}
此外，用于记录 \(L[i][j]\) 来自哪的二维数组 \(W\) 并非是必须的，二维数组 \(W\) 存储的信息可以从 \(L\)、\(X\)、\(Y\) 中推导出来，如果从节省空间的角度考虑，可以撤去二维数组 \(W\)（优化后用于获取所有最长公共子序列的函数 \(sub()\) 便没有用到 \(W\)）。
当不需要输出具体的最长公共子序列，而只需要求最长公共子序列的长度时，可用一滑动数组 \(v\) 替换掉数组 \(L\)。主要代码实现如下：
int main() {
// 输入
cin >> X >> Y;
// 求解并输出
cout << lonComSubSimply();
}
/**
* 使用滑动数组求最长公共子序列长度
* @return 最长公共子序列长度
*/
int lonComSubSimply() {
// 滑动数组v记录当前行，用当前行依次更新下一行的每个单元，当前行初始为v[0...n]=0
int m = X.length(), n = Y.length();
vector<int> v(n + 1, 0);
int lu, left, up; // 下一行单元j的左上、左边、上面单元
for (int i = 0; i < m; ++i) {
lu = left = v[0]; // 下一行单元j的左上和左边初始为v[0]，即0
up = v[1]; // 上边为v[1]
for (int j = 0; j < n; ++j) {
// 更新v
if (X[i] == Y[j])v[j + 1] = lu + 1;
else if (left > up) v[j + 1] = left;
else v[j + 1] = up;
// 更新游标
lu = up, up = v[j + 2], left = v[j + 1];
}
}
return v[n];
}
时间复杂度：\(O(mn)\)。
空间复杂度：\(O(n)\)。
经验总结
动态规划法适用于子问题重叠的情况，即适合解决冗余，并且可以处理不满足贪心准则的问题，一般而言，采用动态规划法解决问题只需要多项式时间复杂度。但是，动态规划法没有统一的标准模型，需要根据问题具有的性质来进行处理，因此，不同问题得到的模型可能不太一样。并且，动态规划法需要存储在求解过程中得到的各种状态信息，因而需要占用较大的存储空间，空间复杂度较之于其它算法较高。动态规划法实质上是一种以空间换时间的技术。
虽然动态规划没有统一的标准模型，但是仍有一些固定的套路。动态规划问题通常有一个 \(dp\) 数组，用来表示所有状态即对应的值，于是，求解动态规划问题就转为定义 \(dp\) 数组和填充 \(dp\) 数组。
定义 \(dp\) 数组需要考虑维度和值。通常 \(dp\) 数组维度与表示一个状态所需变量个数相同，维度应该尽可能少，\(dp\) 数组的值通常为题目所求，如最大值、最小值、计数。
填充 \(dp\) 数组（假设二维，方便后面描述）需要考虑状态转移方程和边界值。得出状态转移方程前，需要分类讨论，即考虑在一般情况下（此时先不要管特殊情况，如边界值）的某个状态 \(dp[i][j]\)，可以通过哪些状态转换而来，分类依据通常可以考虑“包含和不包含”、“包含多少”、“方向”等，分类需要做到不遗漏、不重复（最值问题一般可以重复、计数问题一般不能重复），每种情况均需对应一个 \(dp[x][y]\)，最后根据 \(dp[i][j]\) 与 \(dp[x][y]\) 的关系写出状态转移方程。边界值需要视情况而定，但通常用下标 \(0\) 来存放（一维的 \(dp[0]\)、二维的 \(dp[0][i]\) 和 \(dp[i][0]\)、…），因而填充 \(dp\) 数组时从下标 \(1\) 开始。
对于 \(dp\) 数组，以二维为例，若计算第 \(i\) 行时，只用到 \(dp\) 数组的第 \(i-1\) 行和 \(i\) 行的值，则该二维数组可去掉第一维，转为一维数组。一般而言，填充 \(dp\) 数组需要用到两层循环，计算 \(dp[i][j]\)，\(i\) 从小到大，\(j\) 从小到大，转换之后，\(j\) 可能需要改为从大到小，这从状态转移方程很容易看出需不需要改变方向。
此外，对于不同类型的动态规划问题，也有一些针对性的“经验”。对于线性 \(DP\)，如最长公共子序列问题，划分时通常考虑“前多少”。对于区间 \(DP\)，如矩阵连乘问题，填充 \(dp\) 数组时，第一层循环通常用于枚举长度。对于计数类 \(DP\)，如整数划分问题，分类讨论时，必须做到各情况之间没有交集。对于树形 \(DP\)，如没有上司的舞会问题，通常使用递归。背包问题也是一类经典的DP问题，整数划分问题便可转为完全背包问题求解。
由于动态规划问题没有统一的标准模型，因此求解问题时更依赖于“经验”，所以更需要多看多练多总结，不断地增加“经验”，这样，在处理动态规划问题时才不会无从下手。
END
文章文档：公众号 字节幺零二四 回复关键字可获取本文文档。
浙公网安备 33010602011771号