k-means算法

k：初始中心点个数，计划聚类树 ---->想聚集的个数，中心点也可叫做质点，可以任意选择点数
means:求中心点到其他数据点距离的平均值 ---->采用欧氏距离

方法：
1.确定K，选择k个质心，求每个点到各个质心的距离，判断离哪个最近就归到哪一个


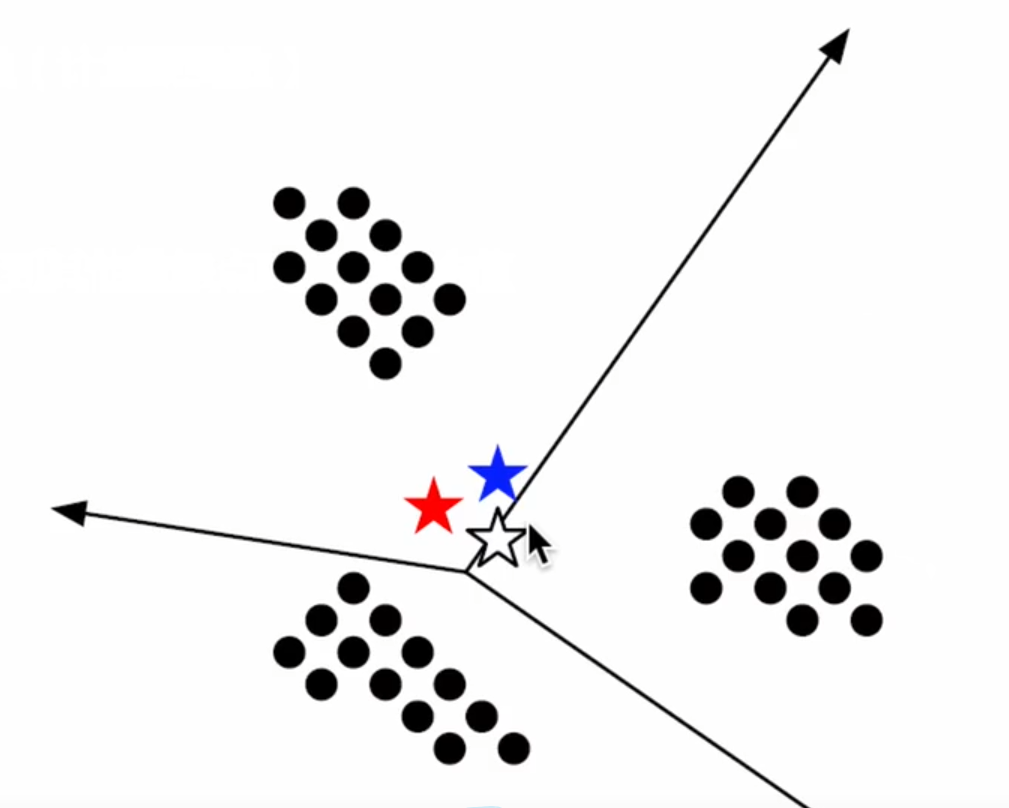
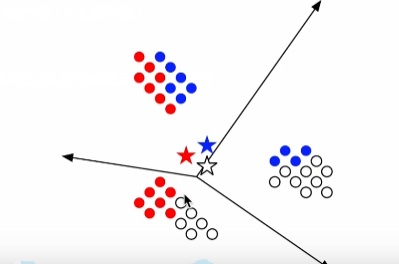
如俩图所示，呈现第一次做完之后的结果，与我们想象的聚类不太一样，效果不太好，是否可以考虑换个质心？

2.将一簇（如红色队列）中的所有点都算一遍，求平均值，将质心可确定为其平均点位置。其他类也按相同处理。

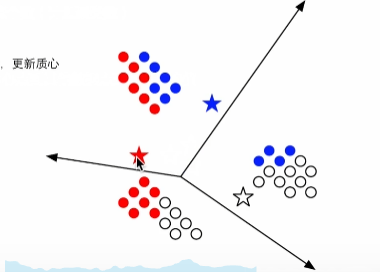
3.更新质心后，重新判断离哪一个质心进，迭代聚类

。
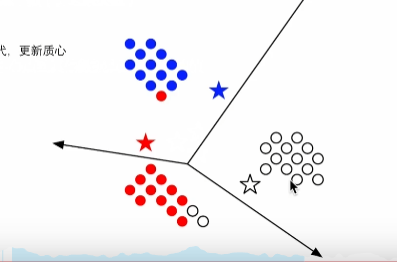
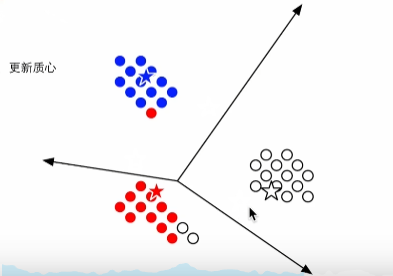4.重复第四步满足收敛要求，直到样本中心点不改变.

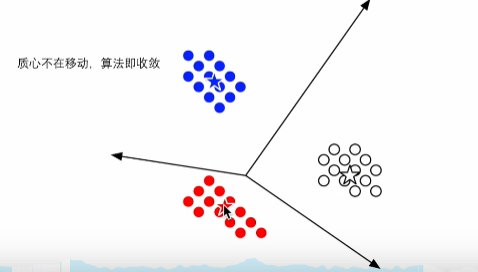
总结算法：
K-Means算法的步骤为：

步骤一：选择任意K个数据，作为各个聚类的质心。
步骤二：对每个样本进行分类，将样本划分到最近的质心所在的类别，执行步骤三。
步骤三：取各个聚类的中心点作为新的质心，执行步骤二进行迭代。

迭代的结束条件：
当新的迭代后的聚类结果没有发生变化。
当迭代次数达到预设的值。

疑问：如果范围比较大，而刚开始有两个中心点选的比较近，可能以后的结果会出现一个中心点逐渐往外移动，有没有一种算法能够第一次就提前将中心点选的比较靠近最终距离？也就是不采取随机选定初始中心点？
其次，感觉效率比较慢，每次都要计算和迭代。