Deepseek核心算法GPRO以及传统算法PPO
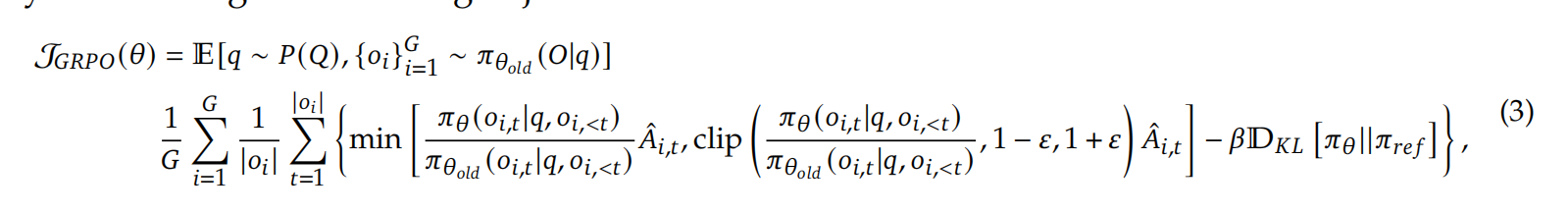

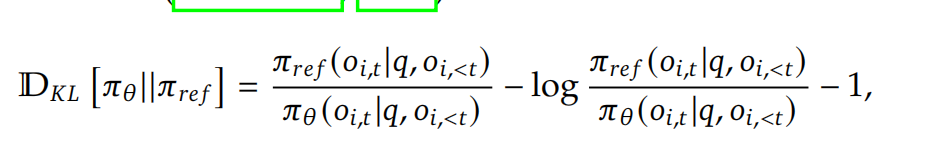
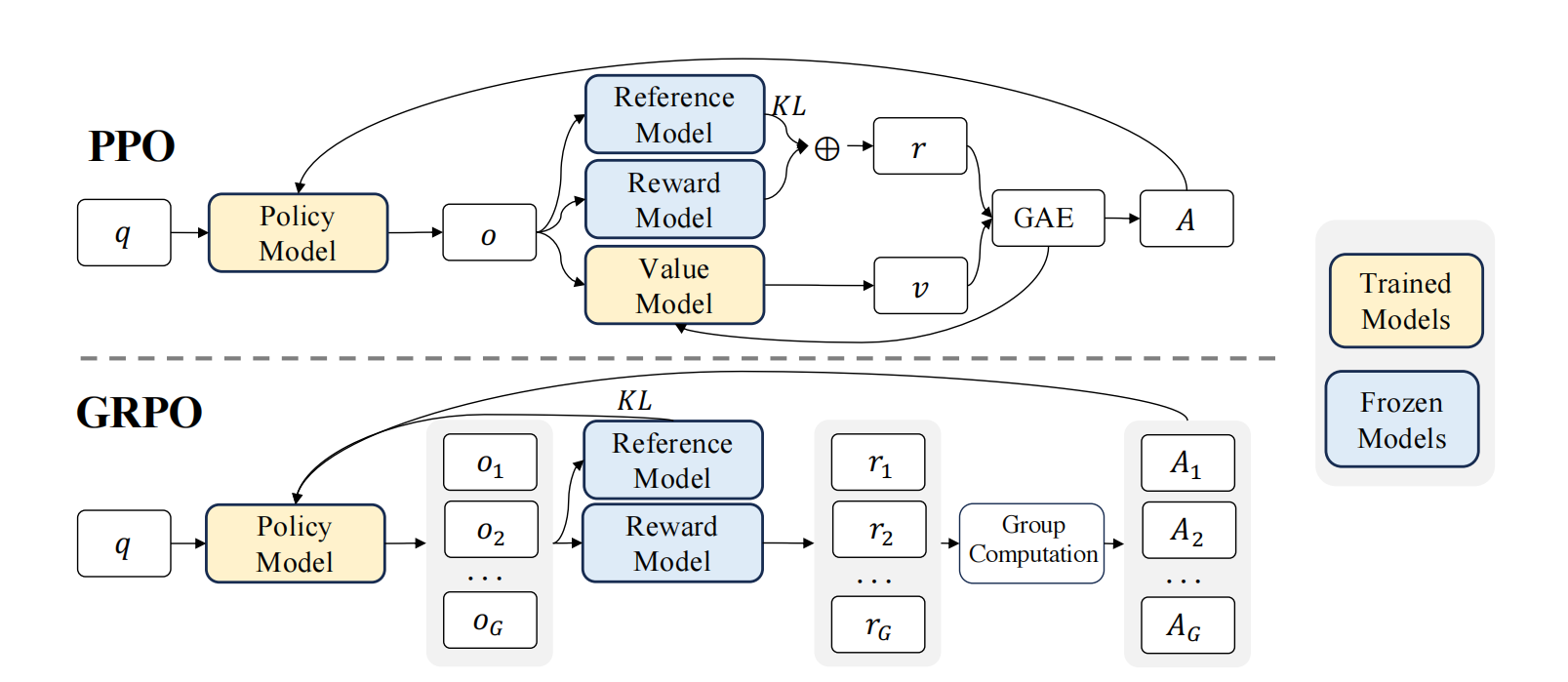
下面是PPO算法:

现在开始讲解GRPO:
1: policy model π_θ ← π_{θ_init}
2: for iteration = 1, ..., I do
3: reference model π_ref ← π_θ
初始策略模型可以是没训练的语言模型。将该模型作为当前的策略模型
4: for step = 1, ..., M do
5: Sample a batch D_b from D 从任务集中随机抽取一批问题
6: Update the old policy model π_{θ_old} ← π_θ 旧策略更新:将当前策略设为旧策略(用于生成参考样本)
7: Sample G outputs {o_i}^G_{i=1} ~ π_{θ_old}(· | q) for each question q ∈ D_b
对每个问题,用旧策略生成 G 个不同的回答
8: Compute rewards {r_i}^G_{i=1} for each sampled output o_i by running r_φ
用奖励模型(自己设计的奖励函数)为每个生成的回答打分.得到r
9: Compute Â_{i,t} for the t-th token of o_i through group relative advantage estimation.
计算每个 token 的组相对优势A(i,t)
采样任务提示:从任务集中随机抽取一批问题。
旧策略更新:将当前策略设为旧策略(用于生成参考样本)。
组采样:对每个问题,用旧策略生成 G 个不同的回答(形成一个 “组”)。
奖励计算:用奖励模型(自己设计的奖励函数)为每个生成的回答打分。
优势估计:计算每个 token 的组相对优势(对比同组内其他回答的平均表现)就是A(i,t)
10: for GRPO iteration = 1, ..., μ do
11: Update the policy model π_θ by maximizing the GRPO objective (Equation 21)
12:Update r_φ through continuous training using a replay mechanism.
策略更新:通过最大化以下目标函数更新策略
奖励模型更新:使用历史样本(经验回放)持续优化奖励模型,提高评估准确性
对于A旁边的β项是为了防止策略变化过大,如果新策略变化更大,该值为负数。奖励值总体变小,防止梯度过大。反之策略变化小则该值变大,总奖励变大,防止梯度下降过多。新旧策略相等则该值为0,不做影响。
最大化奖励,求导就是梯度。
重要理解:1.所谓策略Π实际就是softmax函数,参数就是神经网络的参数。
RL的训练流程为,假设模型生成100个token,对完整的100个token计算获得的奖励R(通过奖励函数)。然后会对每一个token计算到该token获得的奖励Ai+β项,然后求策略梯度梯度(即对神经网络参数求log的导数,再乘softmax导数,在乘神经网络每一层的多项式导数(链式法则)),对每个token的策略梯度乘以完整100token的奖励R作为最后的梯度进行传播。
通俗理解:通过训练条件神经网络的参数,让符合奖励函数中规则的token生成的概率增加。
KL 散度(Kullback-Leibler Divergence),又称相对熵,是衡量两个概率分布之间差异的指标。它在机器学习
PPO与GRPO对比
GRPO简化了PPO中的价值模型,价值模型通常与策略模型规模相当。而grpo通过计算一个问题的多个回答的均值作为奖励模型减少了计算量
PPO中每次输出都会计算参考模型与奖励模型的KL散度,grpo直接将kl散度加入到奖励函数中来减少了模型复杂性。
- old_policy(states)
old_policy 一般是一个自定义的神经网络模型,或者是一个函数,其作用是根据输入的状态 states 输出相应的策略(policy)。
states 是一个输入张量,代表了环境中的状态信息。在强化学习场景中,状态可以是智能体所处环境的各种特征,例如游戏画面的像素值、机器人的关节角度等。
调用 old_policy(states) 会让 old_policy 模型对 states 进行前向传播计算,返回一个输出张量。这个输出张量可能代表了在不同状态下采取各个动作的概率分布等信息。 - .gather
gather 是 PyTorch 张量的一个方法,用于从张量中收集特定索引位置的元素。其函数签名为 torch.gather(input, dim, index, out=None) 。
input:即 old_policy(states) 的输出结果,是要从中收集元素的源张量。
dim:指定要沿着哪个维度进行收集操作。
index:一个与 input 部分维度匹配的索引张量,用于指定要收集的元素的位置。
out(可选):用于存储结果的张量。
DeepSeek的GRPO论文
摘要
由于其复杂且结构化的本质,数学推理对于语言模型来说是一项重大挑战。在本文中,我们介绍了深度求索数学模型70亿参数版本(DeepSeekMath 7B),它基于深度求索代码基础模型v1.5 70亿参数版本(DeepSeek-Coder-Base-v1.5 7B)继续进行预训练,使用了从“常见爬虫数据集”(Common Crawl)中获取的1200亿个与数学相关的词元,同时还结合了自然语言和代码数据。深度求索数学模型70亿参数版本在竞争级别的MATH基准测试中取得了令人印象深刻的51.7%的分数,且不依赖外部工具包和投票技术,接近了谷歌的双子星超大规模模型(Gemini-Ultra)和OpenAI的GPT-4的性能水平。对深度求索数学模型70亿参数版本生成的64个样本进行自一致性处理后,在MATH基准测试中达到了60.9%的分数。深度求索数学模型的数学推理能力归因于两个关键因素:首先,我们通过精心设计的数据选择流程,挖掘了公开可用的网络数据的巨大潜力。其次,我们引入了组相对策略优化算法(Group Relative Policy Optimization,简称GRPO),这是近端策略优化算法(Proximal Policy Optimization,简称PPO)的一种变体,它在优化近端策略优化算法内存使用情况的同时,增强了数学推理能力。
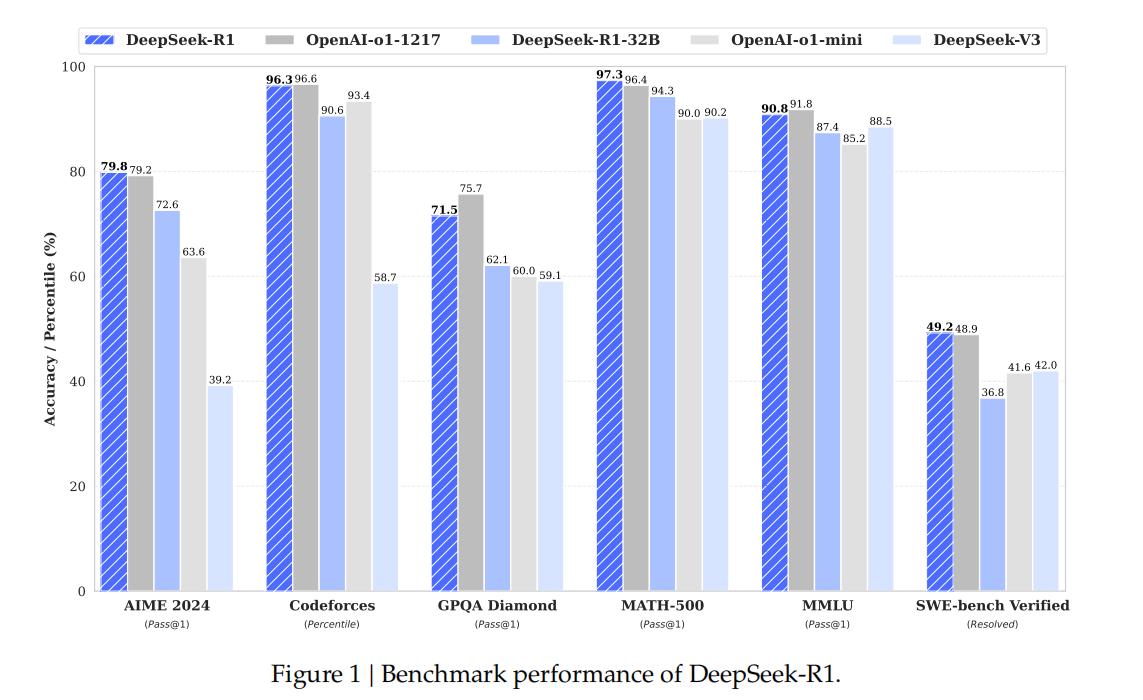
- 引言
大语言模型(LLM)彻底革新了人工智能中数学推理的方法,在定量推理基准测试(亨德里克斯等人,2021年)和几何推理基准测试(特里恩等人,2024年)方面都推动了重大进展。此外,这些模型已被证明在帮助人类解决复杂数学问题方面发挥了重要作用(陶,2023年)。然而,像GPT-4(OpenAI,2023年)和双子星超大规模模型(Gemini-Ultra)(阿尼尔等人,2023年)这样的前沿模型并未公开,而目前可获取的开源模型在性能上远远落后。
在这项研究中,我们介绍了深度求索数学模型(DeepSeekMath),这是一个特定领域的语言模型,它在数学能力方面显著优于开源模型,并且在学术基准测试中接近GPT-4的性能水平。为了实现这一目标,我们创建了深度求索数学语料库(DeepSeekMath Corpus),这是一个大规模的高质量预训练语料库,包含1200亿个数学词元。这个数据集是使用基于快速文本(fastText)的分类器(茹兰等人,2016年)从 “常见爬虫数据集”(Common Crawl,简称CC)中提取的。在初始阶段,使用来自开放网络数学数据集(OpenWebMath)(帕斯特等人,2023年)的实例作为正例来训练分类器,同时纳入各种其他网页作为反例。随后,我们使用该分类器从 “常见爬虫数据集” 中挖掘更多正例,并通过人工标注进一步优化。然后,用这个增强后的数据集更新分类器以提高其性能。评估结果表明,这个大规模语料库质量很高,因为我们的基础模型深度求索数学基础模型70亿参数版本(DeepSeekMath-Base 7B)在GSM8K数据集(科布等人,2021年)上达到了64.2%的成绩,在竞争级别的MATH数据集(亨德里克斯等人,2021年)上达到了36.2%的成绩,超过了米纳erva 5400亿参数模型(Minerva 540B)(莱夫科维茨等人,2022a)。此外,深度求索数学语料库是多语言的,所以我们注意到它在中国的数学基准测试(魏等人,2023年;钟等人,2023年)中也有性能提升。我们认为,我们在数学数据处理方面的经验是研究界的一个起点,并且在未来还有很大的改进空间。
深度求索数学基础模型(DeepSeekMath-Base)以深度求索代码基础模型v1.5 70亿参数版本(DeepSeek-Coder-Base-v1.5 7B)(郭等人,2024年)为初始化模型,因为我们发现,与通用大语言模型相比,从一个代码训练模型开始是更好的选择。此外,我们观察到数学训练也提高了模型在大规模多任务语言理解基准测试(MMLU)(亨德里克斯等人,2020年)和BBH基准测试(苏兹贡等人,2022年)中的能力,这表明它不仅增强了模型的数学能力,还提升了通用推理能力。
在预训练之后,我们使用思维链(Wei等人,2022年)、程序思维(Chen等人,2022年;高等人,2023年)以及工具集成推理(Gou等人,2023年)的数据对深度求索数学基础模型进行数学指令微调。得到的模型深度求索数学指令模型70亿参数版本(DeepSeekMath-Instruct 7B)击败了所有70亿参数的同类模型,并且可与700亿参数的开源指令微调模型相媲美。
此外,我们引入了组相对策略优化算法(Group Relative Policy Optimization,简称GRPO),这是近端策略优化算法(Proximal Policy Optimization,简称PPO)(舒尔曼等人,2017年)的一种强化学习(RL)变体算法。组相对策略优化算法(GRPO)舍弃了评判模型,而是从组分数中估计基线,显著减少了训练资源。通过仅使用英语指令微调数据的一个子集,组相对策略优化算法(GRPO)在强化学习阶段相比强大的深度求索数学指令模型(DeepSeekMath-Instruct)取得了大幅提升,包括在领域内任务(GSM8K数据集:从82.9%提升到88.2%,MATH数据集:从46.8%提升到51.7%)和领域外数学任务(例如,CMATH数据集:从84.6%提升到88.8%)中。我们还提供了一个统一的范式来理解不同的方法,例如拒绝采样微调(Rejection Sampling Fine-Tuning,简称RFT)(袁等人,2023a)、直接偏好优化(Direct Preference Optimization,简称DPO)(拉法伊洛夫等人,2023年)、近端策略优化算法(PPO)和组相对策略优化算法(GRPO)。基于这样一个统一的范式,我们发现所有这些方法都可以被概念化为直接或简化的强化学习技术。我们还进行了广泛的实验,例如在线训练与离线训练对比、结果监督与过程监督对比、单轮强化学习与迭代强化学习对比等等,以深入研究这个范式的关键要素。最后,我们解释了为什么我们的强化学习提升了指令微调模型的性能,并进一步总结了基于这个统一范式实现更有效强化学习的潜在方向。
1.1. 研究贡献
我们的贡献包括可扩展的数学预训练,以及对强化学习的探索和分析。
大规模数学预训练
• 我们的研究提供了有力的证据,表明公开可用的 “常见爬虫数据集”(Common Crawl)数据包含对数学研究有价值的信息。通过实施精心设计的数据选择流程,我们成功构建了深度求索数学语料库(DeepSeekMath Corpus),这是一个高质量的数据集,包含从经过数学内容筛选的网页中提取的1200亿个词元,其规模几乎是米纳erva模型(Minerva)(莱夫科维茨等人,2022a)所使用的数学网页数据规模的7倍,是最近发布的开放网络数学数据集(OpenWebMath)(帕斯特等人,2023年)规模的9倍。
• 我们的预训练基础模型深度求索数学基础模型70亿参数版本(DeepSeekMath-Base 7B)取得了与米纳erva 5400亿参数模型(Minerva 540B)(莱夫科维茨等人,2022a)相当的性能,这表明参数数量并非数学推理能力的唯一关键因素。在高质量数据上进行预训练的较小规模模型也能取得强大的性能。
• 我们分享了数学训练实验的发现。在进行数学训练之前先进行代码训练,提高了模型在使用工具和不使用工具两种情况下解决数学问题的能力。这部分回答了一个长期存在的问题:代码训练能提高推理能力吗?我们认为答案是肯定的,至少对于数学推理是如此。
• 尽管在arXiv论文上进行训练很常见,尤其是在许多与数学相关的研究中,但在本文采用的所有数学基准测试中,这种训练方式并没有带来显著的性能提升。
强化学习的探索与分析
• 我们引入了组相对策略优化算法(Group Relative Policy Optimization,简称GRPO),这是一种高效且有效的强化学习算法。组相对策略优化算法(GRPO)舍弃了评判模型,而是从组分数中估计基线,与近端策略优化算法(Proximal Policy Optimization,简称PPO)相比,显著减少了训练资源。
• 我们证明了组相对策略优化算法(GRPO)仅通过使用指令微调数据,就能显著提升我们的指令微调模型深度求索数学指令模型(DeepSeekMath-Instruct)的性能。此外,我们观察到在强化学习过程中,模型在领域外任务的性能也得到了提升。
• 我们提供了一个统一的范式来理解不同的方法,例如拒绝采样微调(Rejection Sampling Fine-Tuning,简称RFT)、直接偏好优化(Direct Preference Optimization,简称DPO)、近端策略优化算法(PPO)和组相对策略优化算法(GRPO)。我们还进行了广泛的实验,例如在线训练与离线训练对比、结果监督与过程监督对比、单轮强化学习与迭代强化学习对比等等,以深入研究这个范式的关键要素。
• 基于我们的统一范式,我们探究了强化学习有效的背后原因,并总结了几个潜在的方向,以实现对大语言模型更有效的强化学习。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号