数学建模---层次分析法

评价类问题

1、评价目标

2、评价准则

3、有哪些方案

层次分析法

层次分析法 (Analytic Hierarchy Process, 简称 AHP) 是一种将定性分析与定量分析相结合的、系统化的多目标决策分析方法。

简单来说，它的核心思想是： “分而治之” 。当面对一个复杂的、难以直接量化的问题（比如“选哪个城市旅游”、“如何评价员工绩效”）时，AHP 将问题分解为不同的层次（目标、准则、方案），通过两两比较的方式确定权重，最后计算出各个方案的综合得分。

核心逻辑：AHP 的基本架构

在介绍具体流程前，你需要理解 AHP 的“金字塔”结构。

1. 目标层 (Goal): 你的最终目的是什么？（例如：选择最佳旅游地）
2. 准则层 (Criteria): 你判断的标准是什么？（例如：景色、费用、交通、居住环境）
3. 方案层 (Alternatives): 你有哪些选择？（例如：苏杭、云南、西藏）

评价类问题的 AHP 实操流程 (四步法)

如果你正在处理数学建模或实际业务中的评价问题，请严格遵循以下四个步骤：

第一步：建立层次结构模型 (Model Construction)

这是最关键的一步，你需要理清思路，画出层次结构图。

• 确定 目标 （最高层）。
• 确定 评价指标 （中间层）。如果有必要，指标还可以细分为子指标。
• 确定 备选方案 （最低层）。

注意： 这一步通常需要参考相关文献或专家意见来选取合理的指标。

第二步：构造判断矩阵 (Construct Judgment Matrices)

在这个阶段，我们不直接给出权重，而是对指标进行“两两比较”。
我们使用 Saaty 的 1-9 标度法 来量化重要性：

标度	含义
1	两个因素相比，具有同样重要性
3	两个因素相比，前者比后者****稍微重要
5	两个因素相比，前者比后者****明显重要
7	两个因素相比，前者比后者****强烈重要
9	两个因素相比，前者比后者****极端重要
2,4,6,8	上述相邻判断的中间值
倒数	若 A 比 B 重要 3，则 B 比 A 重要 1/3

操作： 针对每一层，构造一个正互反矩阵 。例如，在准则层，我们需要比较“景色”和“费用”哪个更重要，以此类推。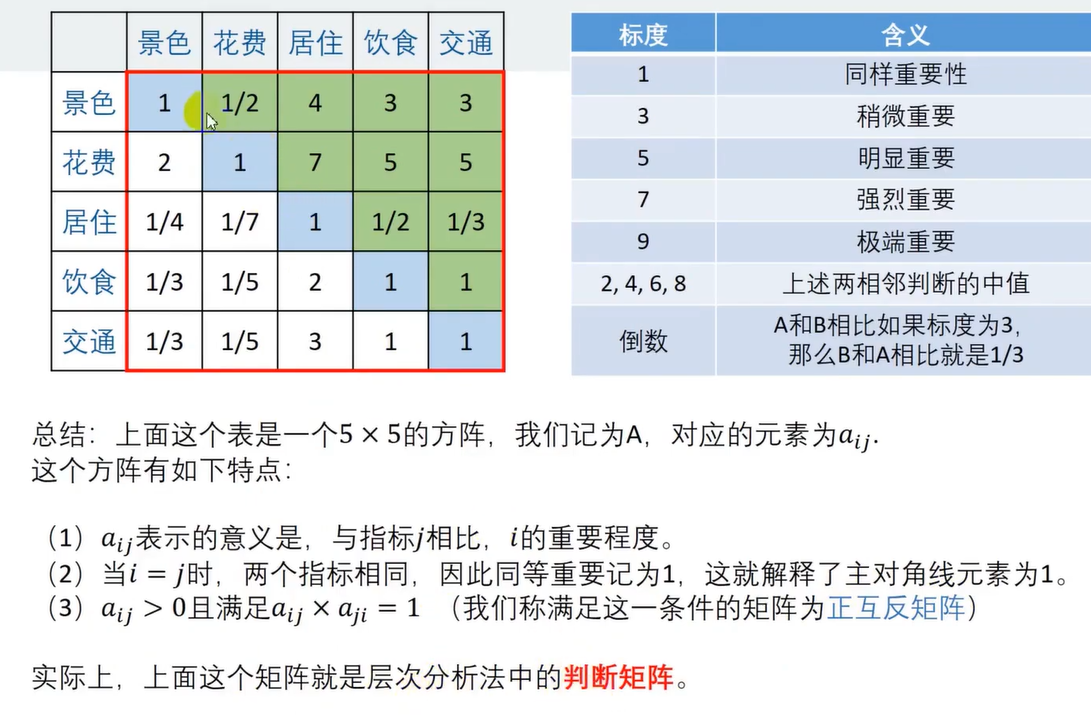

第三步：一致性检验 (Consistency Test)

这是 AHP 中必须要做的一步，否则结果无效。
人类的判断往往是有逻辑漏洞的（例如：认为 A 比 B 好，B 比 C 好，结果又觉得 C 比 A 好）。我们需要通过数学方法检验你的判断矩阵是否存在严重的逻辑矛盾。

流程如下：

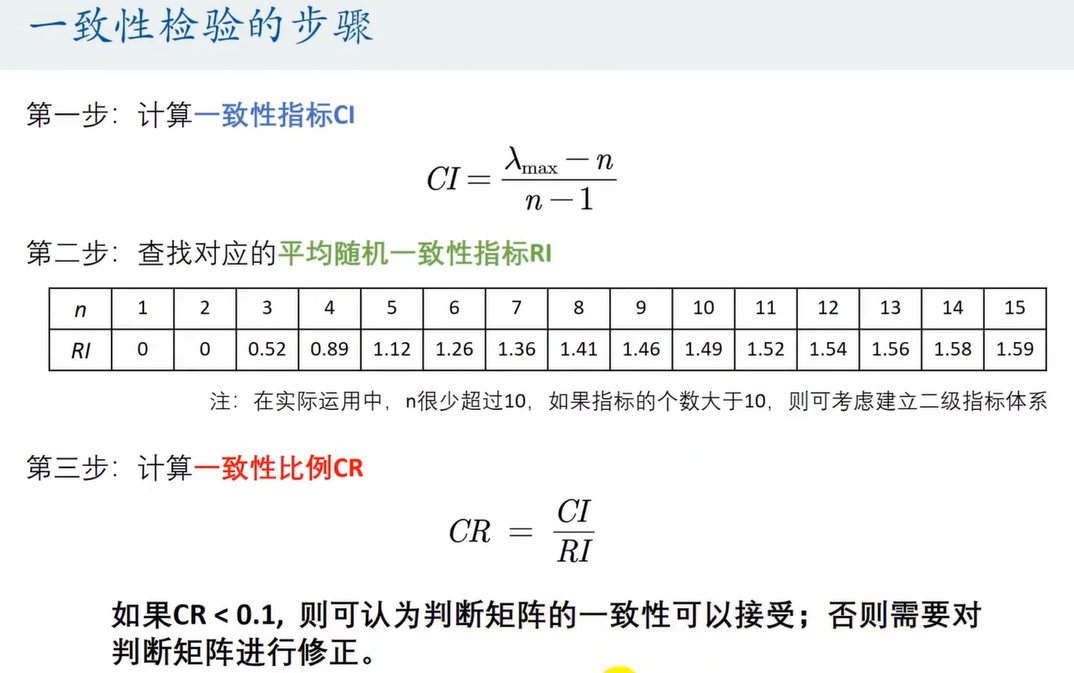
判定标准：

• 若 ，则认为判断矩阵的一致性可以接受。
• 若 ，则需要对判断矩阵进行修正（调整 1-9 的打分）。

第四步：计算权重与得分 (Calculate Weights & Score)

通过一致性检验后，就可以计算权重了。常用的方法有三种（算术平均法、几何平均法、特征值法），其中****特征值法最为常用。

1. 计算准则权重： 根据准则层的判断矩阵，计算出各指标占总目标的权重向量 。
2. 计算方案权重： 针对每一个准则，计算各方案在该准则下的得分。
3. 综合评分： 将（方案在各准则下的得分）乘以（各准则的权重），最后求和。

总结与建议

• 优点： 逻辑清晰，将主观判断数学化，适合缺乏历史数据的问题。
• 缺点： 主观性较强（1-9 打分依赖专家或个人经验），指标过多时计算量大且容易通不过一致性检验（建议指标不超过 9 个）。

---