Codeforces Round 1069 (Div. 2)

因为各种原因，最近几天的做题量与强度有所下降，时间不多了希望未来可以更加努力，以此为戒

B

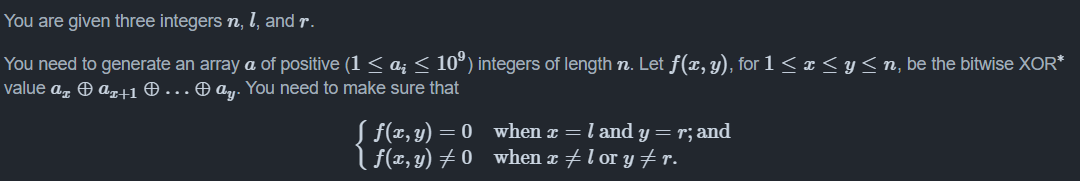
 这一套的难度感觉划分的不太对，这个B题反而比C题难得多

这个B题的思维还是挺巧妙的，显然是个构造，我竟然没有想出来

异或这个知识点有时候和前缀和，后缀和联系挺紧密

构造规则是造一个数组1-n，ai

给出两个端点l，r在l，l+1，l+2，r这个区间里面，异或和为0，其余都不准为0

如果思考一个前缀和异或

F(a,b)=pre[a-1]^pre[b]

也就有

F(l,r)=pre[l-1]^pre[r]=0,也就是pre[l-1]=pre[r]

然后就没有了，我们强制规则一下这两个pre相等即可，然后pre[i]=i就可以解决问题，好巧妙

C

读题到Accepted只用了20分钟，这才是合格的acmer（虽然题目很水）

 两个字符串你要把t排序一下，然后让t中存在子序列=s

你有两种选择往当前ans里面push S字符串的当前位置，或者push进去当前最小的其他不重要的字符

当时思考到问题就是在s字符穿内部把t的字符都插入进去，贪心一下即可

void solve(){
    string t,s,ans;cin>>s>>t;
    map<char,int>mp;
    for(auto it:t)mp[it]++;
    for(auto it:s){
        mp[it]--;
        if(mp[it]<0){
            cout<<"Impossible"<<endl;
            return ;
        }
    }
    vector<char>st;
    for(auto i='a';i<='z';i++)for(int j=1;j<=mp[i];j++)st.push_back(i);
    int stl=0,sl=0;
    while(ans.size()<t.size()){
        if(stl==st.size()){
            ans.push_back(s[sl++]);
        }
        else if(sl==s.size()){
            ans.push_back(st[stl++]);
        }else{
            if(st[stl]<s[sl]){
                ans.push_back(st[stl++]);
            }else{
                ans.push_back(s[sl++]);
            }
        }
    }
    cout<<ans<<endl;
    return ;
}

D 已补

这个题感觉难度好大，超出了我的能力范围

首先读完题后的构思中，没有深刻理解到k取值范围的含义(k<=360)没有想k的次方思考，一直在思考如何用O(N*K)来完成，虽然看起来比较蠢

题目看起来很典型，题意很清晰所以没有观察到内在规律，终没战胜，看了dalao的代码之后才后知后觉

首先给了ai为每一位的上限，所以我们构造的a数组最好是一个单调递增的

所以根据一条规则我们可以得到一个变化而来的数组，我们考虑用一个pos数组来存i位数字最早出现的位置，比如说

1 3 2 5 1

pos[1]=1,  pos[2]=2,  pos[3]=2, pos[4]=4, pos[5]=4  (因为最大是ai所以类似于3，就可以让他等于2或者3来更新pos)

然后考虑如何在规定时间复杂度下把每一个状态都保存下来，和如何计算幸福值

幸福值：

这是一个阶梯状态的值，所以我们可以倒推

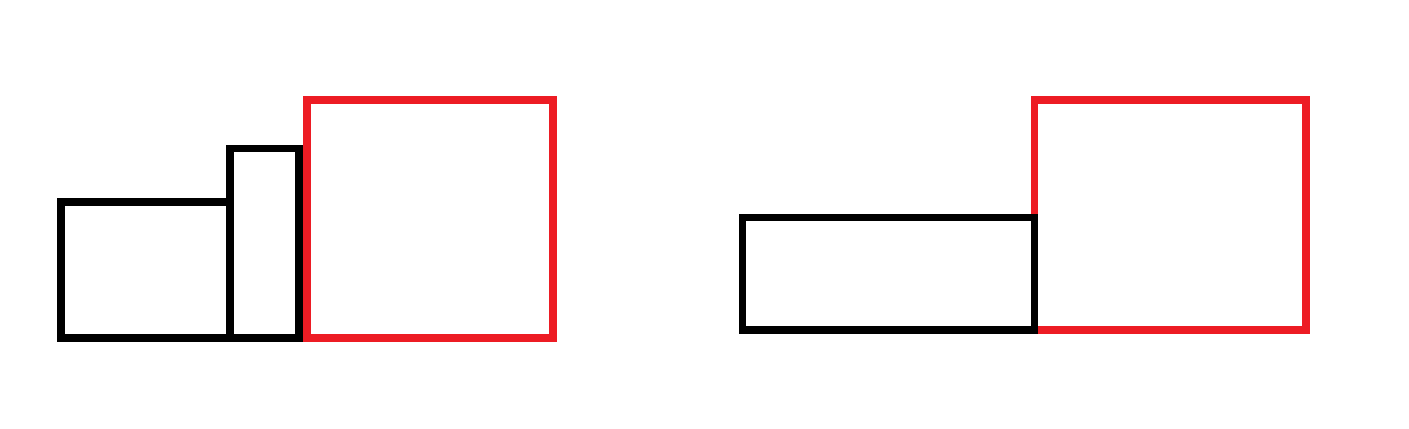
我们观察这两个图像，可以知道如果我们确定了当前数列的最大值，他后面不会有比他更大的值了，所以说他可以提供的幸福值就是红色方块

我们现在只需要知道前面黑色方块的最大面积就好了，黑色的最大面积可以这样来算

我们设当前最大值为u，我们去遍历最大值v=[0,u)，然后面积就等于到达v的面积加上v*(pos[u]-pos[v]),也就是图下绿色的面积

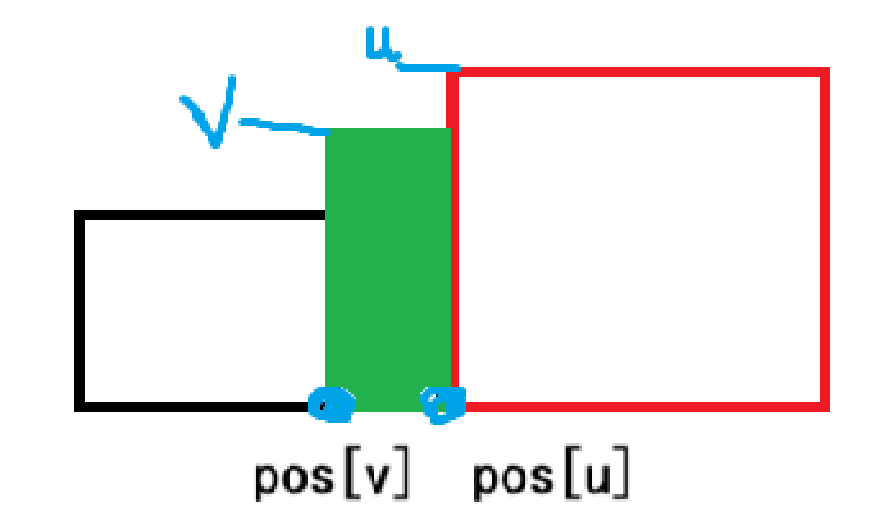
 这样遍历完所有可能的黑色面积之后，我们取最大的作为dp，然后幸福值：dp+u*(n-pos[u]+1)，然后我们取最大的那一个幸福值就好了

理论是这样的，然后我们构造dp数组，对于一个dp[i][j]

我们让i为当前的最大值，j为构成这个数组所消耗的个数

而且dp[i][j]存的内容就是从1-pos[i]的最大面积，也就是最大的黑色面积

对于一个dp[i][j]我们都可以去找一个v=[0,i) 以及消耗use=j-i （为什么前一个的状态是j-i，是因为我们要在不变动前面黑色状态的前提下再消耗i个，来构成当前的最大值）

所以得到地推公式dp[i][j]=MAX(dp[i][j],   dp[v][use]+v*(pos[u]-pos[v])  );

当然这个v*(pos[u]-pos[v])就是我们上图那一个绿色的部分他是前状态到当前状态新增加的价值

我们只需要得到最大的dp[i][j]后，然后再加上红色方块的面积，就可以得到当前最大值为i，消耗格子总数为j的时候的幸福值

ans=max(ans, dp[i][j]+u*(n-pos[u]+1)  )

然后通过这种方式我们就遍历完成了所有情况复杂度O(k^3)

void solve(){
    int n,k;cin>>n>>k;
    vector<int>sh(n+1),pos(k+1,-1);
    int mx=0;
    for(int i=1;i<=n;i++){
        cin>>sh[i];
        while(sh[i]>mx)pos[++mx]=i;
    }
    int ans=0;
    vector<vector<int>>dp(k+1,vector<int>(k+1,-1));
    dp[0][0]=0;
    for(int v=1;v<=k;v++){
        if(pos[v]==-1)break;
        for(int j=v;j<=k;j++){
            for(int u=0;u<v;u++){
                int fa=j-v;
                if(dp[u][fa]==-1)continue;
                int temp=dp[u][fa]+u*(pos[v]-pos[u]);
                dp[v][j]=max(dp[v][j],temp);
            }
            ans=max(ans,dp[v][j]+v*(n-pos[v]+1));
        }
    }
    cout<<ans<<"\n";
    return ;
}

E （前面的区域等以后再来探索吧）