（动态规划）剑指 Offer 14- II. 剪绳子 II

题目描述：

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m - 1] 。

请问 k[0]*k[1]*...*k[m - 1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

 

 

 

提示：

• 2 <= n <= 1000

 

 

 

 

 

 

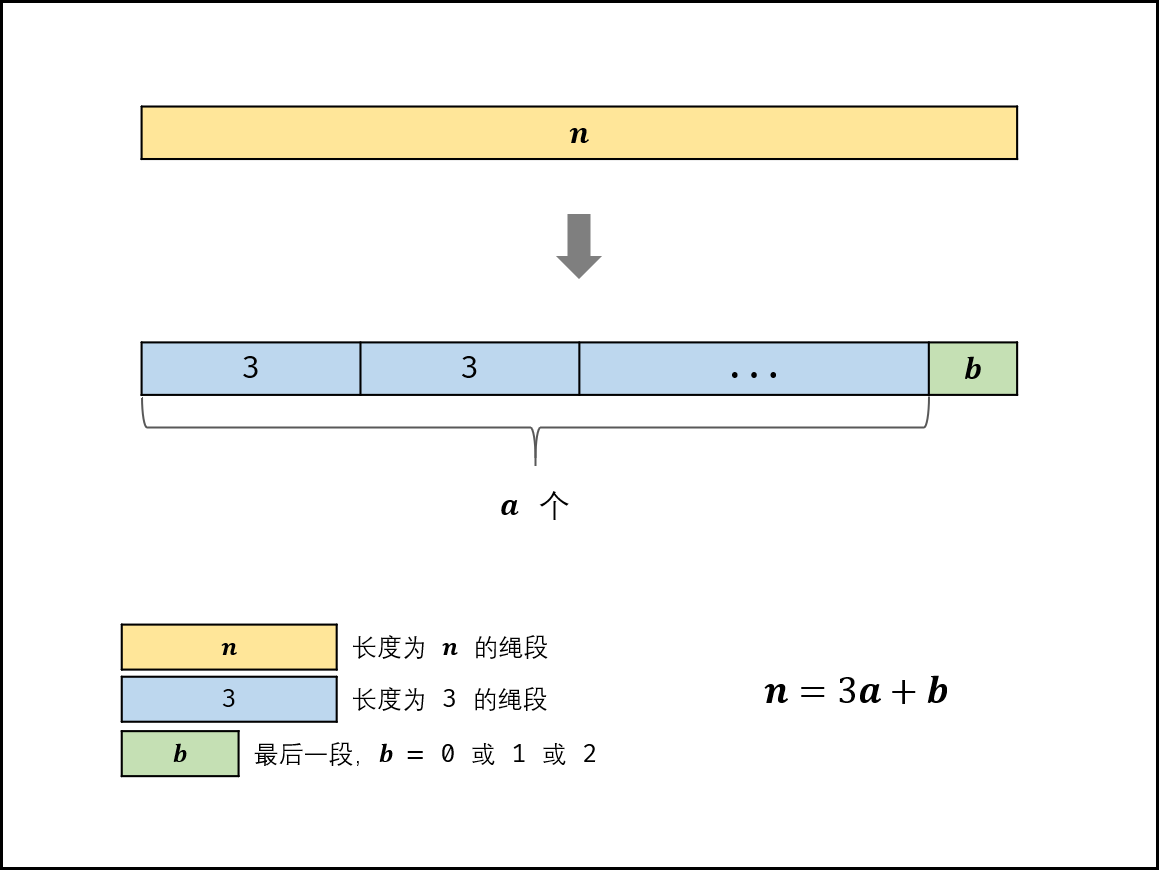
class Solution {
    public int cuttingRope(int n) {
        if(n <= 3) return n - 1;
        long res=1L;
        int p=(int)1e9+7;
        //贪心算法，优先切三，其次切二
        while(n>4){
            res=res*3%p;
            n-=3;
        }
        //出来循环只有三种情况，分别是n=2、3、4
        return (int)(res*n%p);
    }
}