树：剑指 Offer 27. 二叉树的镜像

题目描述：

请完成一个函数，输入一个二叉树，该函数输出它的镜像。

 

例如输入：

     4
   /   \
  2     7
 / \   / \
1   3 6   9
镜像输出：

     4
   /   \
  7     2
 / \   / \
9   6 3   1

 

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

 

限制：

　　0 <= 节点个数 <= 1000

 

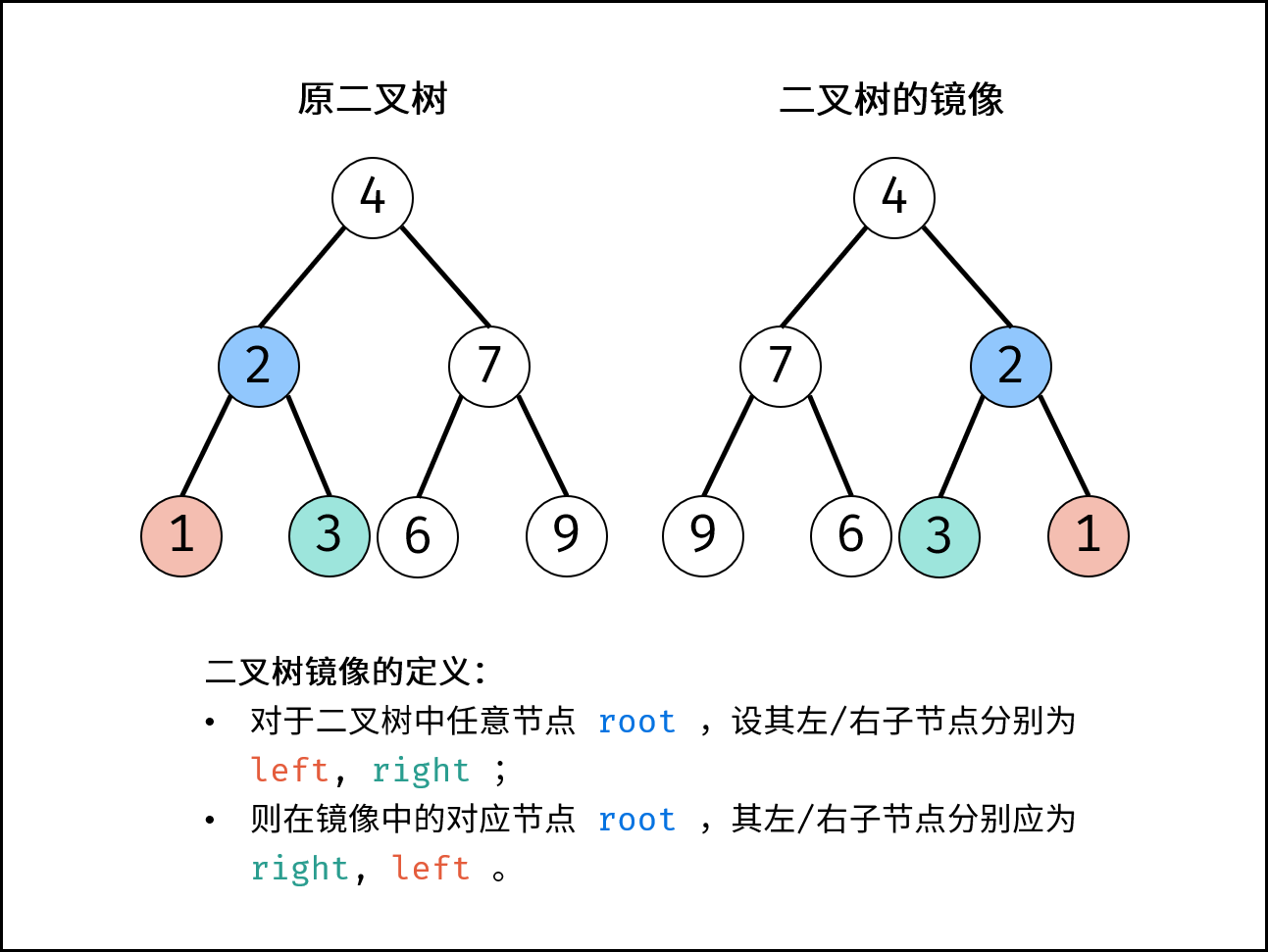
二叉树镜像定义： 对于二叉树中任意节点 root ，设其左 / 右子节点分别为 left, right ；

则在二叉树的镜像中的对应 root 节点，其左 / 右子节点分别为 right, left 。

 

递归法

• 根据二叉树镜像的定义，考虑递归遍历（dfs）二叉树，交换每个节点的左 / 右子节点，即可生成二叉树的镜像。

 

递归解析：
1.终止条件： 当节点 root 为空时（即越过叶节点），则返回 null ；
2.递推工作：
　　1).初始化节点 tmp ，用于暂存 root 的左子节点；
　　2).开启递归 右子节点 mirrorTree(root.right) ，并将返回值作为 root 的 左子节点 。
　　3).开启递归 左子节点mirrorTree(tmp) ，并将返回值作为 root 的 右子节点 。
3.返回值： 返回当前节点 root ；

 

Q： 为何需要暂存 rootroot 的左子节点？
A： 在递归右子节点 “root.left = mirrorTree(root.right);” 执行完毕后， root.left 的值已经发生改变，此时递归左子节点 mirrorTree(root.left) 则会出问题。

复杂度分析：
　　时间复杂度 O(N) ： 其中 N 为二叉树的节点数量，建立二叉树镜像需要遍历树的所有节点，占用O(N) 时间。
　　空间复杂度 O(N) ： 最差情况下（当二叉树退化为链表），递归时系统需使用 O(N) 大小的栈空间。

 

class TreeNode{
    int val;
    TreeNode left;
    TreeNode right;
    public TreeNode(int x) {
        val = x;
    }
}

 

class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        if(root == null) return null;
        TreeNode tmp = root.left;
        root.left = mirrorTree(root.right);
        root.right = mirrorTree(tmp);
        return root;
    }
}

 

另解：

class Solution{
    public TreeNode mirrorTree(TreeNode root){
        if(root==null) return null;
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
        mirrorTree(root.left);
        mirrorTree(root.right);
        return root;
    }
}