栈&队列：剑指 Offer 59 - I. 滑动窗口的最大值

题目描述：

给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。

 

示例:

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7] 
解释: 

  滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

 

提示：

你可以假设 k 总是有效的，在输入数组 不为空 的情况下，1 ≤ k ≤ nums.length。

 

解题思路：

 

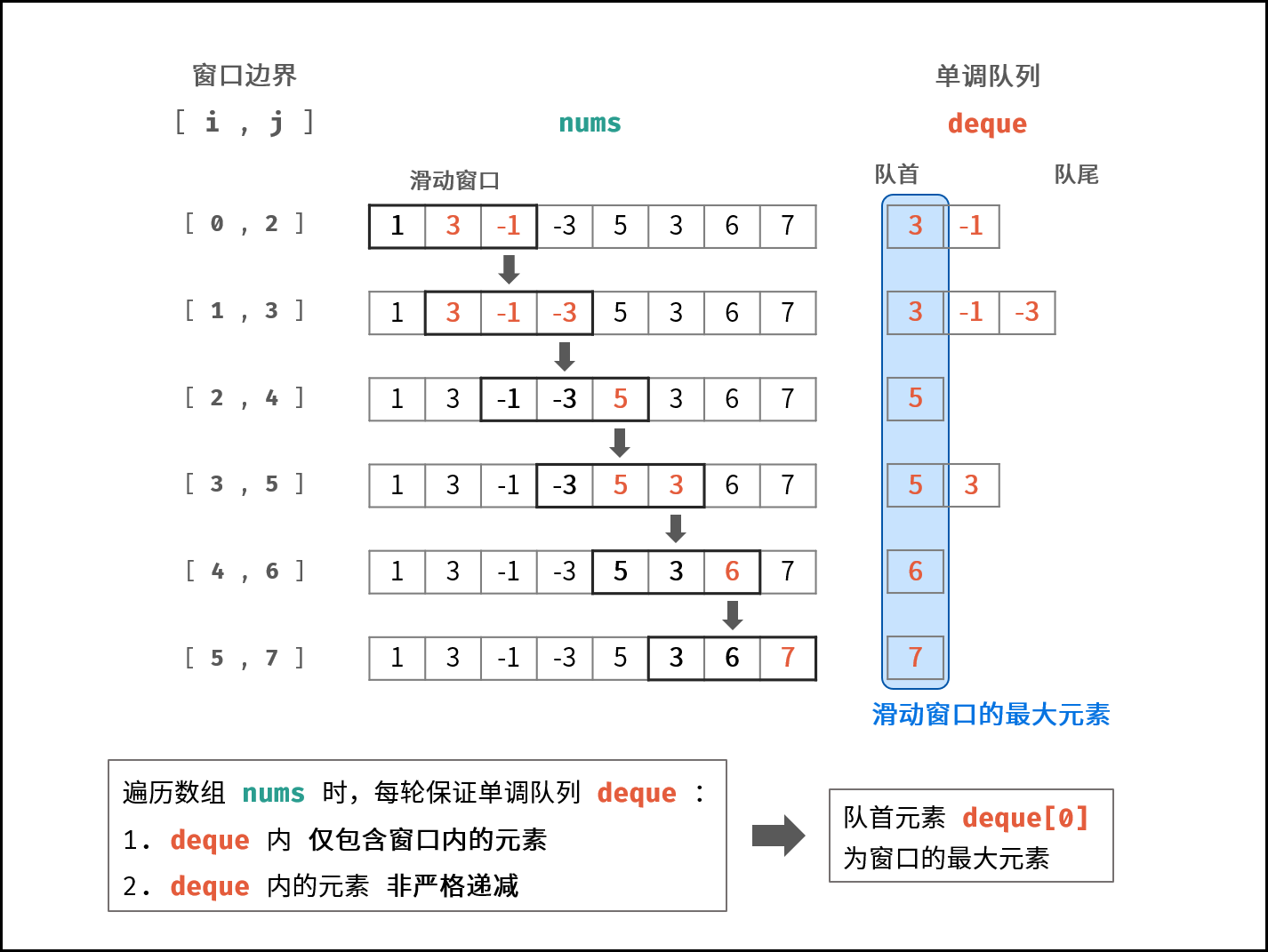
窗口对应的数据结构为 双端队列 ，本题使用 单调队列 即可解决以上问题。遍历数组时，每轮保证单调队列 deque ：

　　1.deque 内 仅包含窗口内的元素 ⇒ 每轮窗口滑动移除了元素 nums[i−1] ，需将 deque 内的对应元素一起删除。
　　2.deque 内的元素 非严格递减 ⇒ 每轮窗口滑动添加了元素 nums[j+1] ，需将 deque 内所有 <nums[j+1] 的元素删除。

 

算法流程：
1.初始化： 双端队列 deque ，结果列表 res，数组长度 n ；
2.滑动窗口： 左边界范围i∈[1−k,n−k] ，右边界范围j∈[0,n−1] ；
　　1).若 i>0 且 队首元素 deque[0] = 被删除元素 nums[i - 1]：则队首元素出队；
　　2).删除 deque内所有 <nums[j] 的元素，以保持 deque 递减；
　　3).将 nums[j] 添加至 deque 尾部；
　　4).若已形成窗口（即 i≥0 ）：将窗口最大值（即队首元素 deque[0] ）添加至列表 res ；
返回值： 返回结果列表 res ；

复杂度分析：
　　时间复杂度 O(n) ： 其中 n 为数组 nums 长度；线性遍历 nums 占用 O(n) ；每个元素最多仅入队和出队一次，因此单调队列 deque 占用 O(2n)。
　　空间复杂度 O(k) ： 双端队列 deque 中最多同时存储 k 个元素（即窗口大小）。

 

class Solution{
    public int[] maxSlidingWindow(int nums[],int k){
        if(nums.length==0||k==0) return new int[0];
        Deque<Integer> deque = new LinkedList<>();//
        int res[] = new int[nums.length-k+1];
        int index=0;//res数组计数
        //未形成窗口区间
        for(int i=0;i<k;i++){
            //队列不为空时，当前值与队列尾部值比较，如果大于，删除队列尾部值
            //一直循环删除到队列中的值都大于当前值，或者删到队列为空
            while(!deque.isEmpty()&&deque.peekLast()<nums[i]){
                deque.removeLast();
            }
            //执行完上面的循环后，队列中要么为空，要么值都比当前值大，然后就把当前值添加到队列中
            deque.addLast(nums[i]);
        }
        //窗口区间刚形成后，把队列首位值添加到队列中
        //因为窗口形成后，就需要把队列首位添加到数组中，而下面的循环是直接跳过这一步的，所以需要我们直接添加
        res[index++] = deque.peekFirst();
        //形成滑动窗口
        for (int i=k;i<nums.length;i++){
            //i-k是已经在区间外了，如果首位等于nums[i-k]，那么说明此时首位值已经不再区间内了，需要删除
            if(deque.peekFirst()==nums[i-k]){
                deque.removeFirst();
            }
            //删除队列中比当前值大的值
            while (!deque.isEmpty()&&deque.peekLast()<nums[i]){

                deque.removeLast();
            }
            //把当前值添加到队列中
            deque.addLast(nums[i]);
            //把队列的首位值添加到arr数组中
            res[index++] = deque.peekFirst();
        }
        return res;
    }
}