【笔记】机器学习基础 - Ch6.1-4 Kernel Methods

6.1 Introduction

继续从二分类模型出发，实际情况中样本通常不是线性可分的
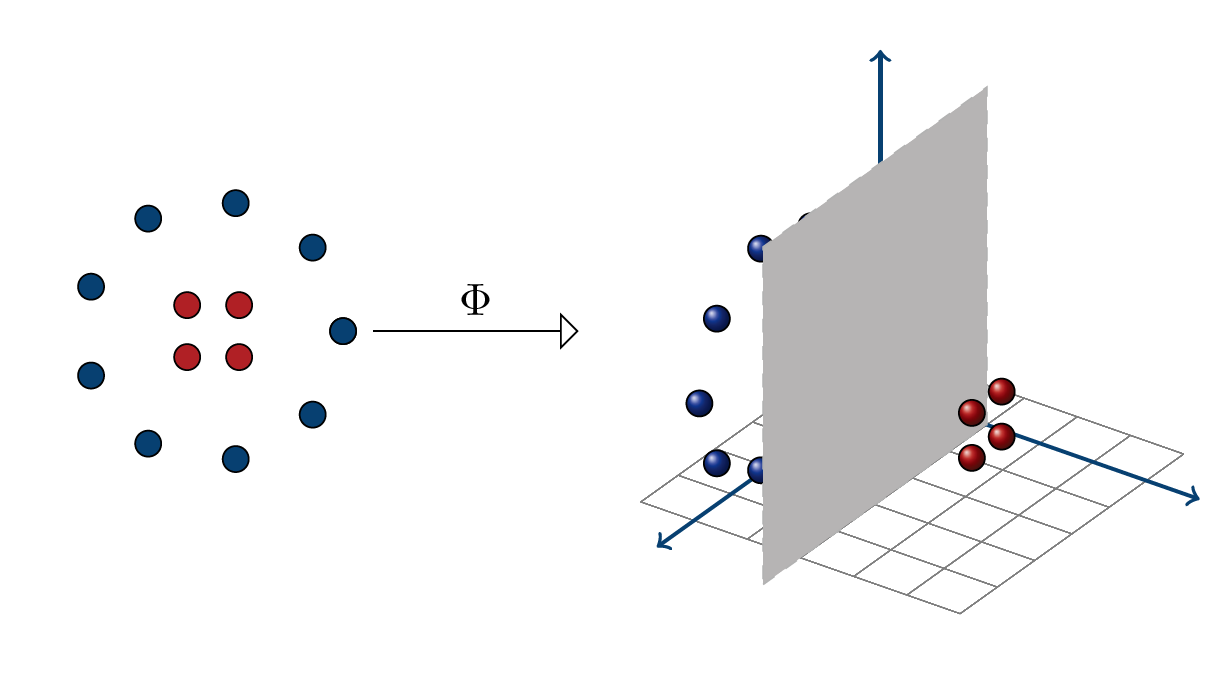
一种思路是增大特征空间的维度，也就是加入原本特征的组合，即一个从 \(\cal X\) 到更高维 \(\mathbb{H}\) 的非线性映射 \(\Phi:\cal X\to \mathbb{H}\)，从而在 \(\mathbb{H}\) 可能变得线性可分；尽管 SVM 对有界向量提出的上界和特征空间的维度无关，但是内积的计算量会增大；
改进之，注意到一些算法只用到向量内积，因此可以跳过映射 \(\Phi\) 一步到位，因此引入核方法 kernel methods

Def. Kernels
函数 \(K:{\cal X\times X}\to \mathbb{R}\) 称为 \(\cal X\) 上的核 kernel

引入核的思想，是为了在内积上等价于某个映射 \(\Phi:\cal X\to \mathbb{H}\)；且 \(K\) 的计算量要小于映射+高维空间内积（例如 \(O(N),O(\dim(\mathbb{H}))\)，甚至 \(\dim(\mathbb{H})\) 无穷大）

\[\forall x, y\in {\cal X},\quad K(x, y)=\lang \Phi(x), \Phi(y)\rang \]

设计核 \(K\) 时，我们只要能够保证对应有那么个 \(\Phi\) 存在就行了，比如 \(K\) 满足 Mercer's condition，或者更一般地，\(K\) 满足正定对称 positive definite symmetric (PDS)

6.2 Positive definite symmetric kernels

Def. Positive definite symmetric kernels (PDS kernels)
核 \(K:{\cal X\times X}\to \mathbb{R}\) 称为正定对称的 positive definite symmetric (PDS)，若对于任意样本 \(S=(x _1,\dotsb, x _m)\sube\cal X\)，矩阵 \({\bf K}=[K(x _i, x _j)] _{ij}\) 是对称半正定的 symmetric positive semidefinite (SPSD)，即 \(\bf K\) 对称，且满足以下两者之一：

• \(\bf K\) 的特征值都非负
• 任意向量 \({\bf c}\in \mathbb{R} ^{m}\)，有二次型 \({\bf c'Kc}=\sum _{i,j}K(x _i, x _j) c _i c _j\ge 0\)

此时 \(\bf K\) 也称为样本 \(S\) 的核矩阵 kernel matrix 或者 Gram matrix
观察，实际上从等价内积看，记 \(\Phi(S) _{m\times \dim(\mathbb{H})}=[\Phi(x _1)',\dotsb, \Phi(x _m)']'\)，有 \({\bf K}=\Phi(S)\Phi(S) ^T\)，从而二次型 \({\bf c'Kc}=\lang\Phi(S)'{\bf c},\Phi(S)'{\bf c}\rang\ge 0\)；更确切的原因在之后的 RKHS 会给出
常见 PDS kernel 有：

Polynomial kernels 多项式核

对任意 \(c>0\)，\(\mathbb{R} ^N\) 上的度为 \(d\in \mathbb{N}\) 的多项式核 \(K\)，形如

\[\forall {\bf x, y}\in \mathbb{R} ^N,\quad K({\bf x, y}) = ({\bf x\cdot y} + c) ^d \]

这是什么？展开一下：

\[\begin{aligned} ({\bf x\cdot y} + c) ^d &=(x _1 y _1+\dotsb + x _N y _N+c) ^d \\ &=\sum _{\sum k=d} C _{d} ^{k _0} C _{d-k _0} ^{k _1}\dotsb C _{d-\sum ^{N-1} k} ^{k _N}\cdot c ^{k _0}(x _1 y _1) ^{k _1}\dotsb(x _N y _N) ^{k _N} \\ &=\sum _{\sum k=d}\frac{d!}{k _0!k _1!\dotsb k _N !}\cdot \left(\sqrt{c} ^{k _0} x _1 ^{k _1} \dotsb x _N ^{k _N} \right)\cdot \left(\sqrt{c} ^{k _0} y _1 ^{k _1} \dotsb y _N ^{k _N} \right) \\ &=\begin{bmatrix}\vdots \\ \sqrt{\frac{d!}{k _0!k _1!\dotsb k _N !}}\sqrt{c} ^{k _0} x _1 ^{k _1} \dotsb x _N ^{k _N} \\ \vdots \end{bmatrix} _{C _{N+d} ^d \times 1} \cdot \begin{bmatrix} \vdots \\ \sqrt{\frac{d!}{k _0!k _1!\dotsb k _N !}}\sqrt{c} ^{k _0} y _1 ^{k _1} \dotsb y _N ^{k _N} \\ \vdots \end{bmatrix} _{C _{N+d} ^d \times 1} \\ &= \lang\Phi _{c, d}({\bf x}),\Phi _{c, d}({\bf y})\rang \end{aligned} \]

可见，度为 \(d\) 的核 \(K\)，对应 \(N\) 维到 \(C _{N+d} ^d\) 维的映射 \(\Phi _{c, d}\)，且新的特征为原本特征的所有阶至多为 \(d\) 的单项式 monomials
例如，对于四个点 \((\pm 1,\pm 1)\) 线性不可分的亦或函数，只需要取 \(d=2\)，然后就存在分界面 \(x _1x _2=0\) 了

Gaussian kernels 高斯核

对任意 \(\sigma>0\)，\(\mathbb{R} ^N\) 上的高斯核或称 radial basis function (RBF) \(K\)，形如

\[\forall {\bf x, y}\in \mathbb{R} ^N,\quad K({\bf x, y})=\exp\left( -\frac{\Vert {\bf x-y}\Vert ^2}{2\sigma ^2} \right) \]

可以证明，它们是 PDS 核，且可由核 \(K':({\bf x, y})\mapsto\exp(\frac{\bf x\cdot y}{\sigma ^2})\) 通过规范化 normalization 导出
而 \(K'\) 可展开为幂级数：\(K'({\bf x, y})=\sum _{n=0} ^{\infty}\frac{({\bf x\cdot y}) ^n}{n!\sigma ^{2n}}\)，可见 \(K'\) 和高斯核可以代表一些无穷阶的多项式，因此也是最常用的核

核 \(K\) 规范化 normalization 得到 \(K _\text{norm}\)，定义为

\[\forall{\bf x, y}\in {\cal X},\quad K _\text{norm}({\bf x, y})=\begin{cases} 0 & K({\bf x, x})K({\bf y, y})=0 \\ \frac{K({\bf x, y})}{\sqrt{K({\bf x, x})K({\bf y, y})}} & \text{otherwise}\end{cases} \]

后面会证明，PDS 核规范化后也是 PDS 核
且核 \(K':({\bf x, y})\mapsto\exp(\frac{\bf x\cdot y}{\sigma ^2})\) 是 PDS 核（因为是 PDS 核的幂级数，见后），其规范化后就是高斯核

\[\frac{K'({\bf x, y})}{\sqrt{K'({\bf x, x})K'({\bf y, y})}}=\frac{\exp(\frac{\bf x\cdot y}{\sigma ^2})}{\exp(\frac{\Vert\bf x\Vert ^2}{2\sigma ^2})\exp(\frac{\Vert\bf y\Vert ^2}{2\sigma ^2})}=\exp\left( -\frac{\Vert {\bf x-y}\Vert ^2}{2\sigma ^2} \right) \]

Sigmoid kernels

对任意 \(a,b\ge 0\)，\(\mathbb{R} ^N\) 上的 sigmoid 核 \(K\)，形如

\[\forall {\bf x, y}\in \mathbb{R} ^N,\quad K({\bf x, y})=\tanh(a({\bf x\cdot y})+b) \]

SVM + sigmoid 核，也可用该式定义简单神经网络，两者有所关联。当 \(a<0\vee b<0\) 时该核就不是 PDS 核，对应的神经网络也不再有凸优化收敛的保证。

再生核希尔伯特空间，Reproducing kernel Hilbert space (RKHS)

Hilbert 空间可以参考文末附
给出 PDS 核的一些重要性质，并借此说明它类比于 Hilbert 空间的内积

Lemma. Cauchy-Schwarz inequality for PDS kernels
PDS 核 \(K:{\cal X\times X}\to \mathbb{R}\)，则

\[\forall {\bf x, y}\in {\cal X},\quad K({\bf x, y}) ^2\le K({\bf x, x})K({\bf y, y}) \]

这个式子可以方便我们感受一下 PDS，比如根据定义有 \(K({\bf x,x})\ge 0\)，若 \(K({\bf x,x})= 0\)，则任意 \(\bf y\) 都有 \(K({\bf x,y})=0\)

证明，注意到 PDS 核定义，样本 \(S=({\bf x, y})\) 的核矩阵 \({\bf K}\) 的特征值非负，即特征值乘积 \(\det({\bf K})\) 非负，也就是 \(K({\bf x, x})K({\bf y, y})-K({\bf x, y}) ^2\ge 0\)，得证

Th. Reproducing kernel Hilbert space (RKHS)，再生核希尔伯特空间
PDS 核 \(K:{\cal X\times X}\to \mathbb{R}\)，则存在一个元素为 \({\cal X}\to\mathbb{R}\) 的映射的 Hilbert 空间 \(\mathbb{H}\) 和映射 \(\Phi:\cal X\to\mathbb{H}\)，使得内积为

\[\forall {x, y}\in {\cal X},\quad \lang \Phi({ x}), \Phi({ y})\rang=K({x, y}) \]

例如，我们可以取映射 \(\Phi(x):x'\mapsto K(x,x')\)，则集合 \(\mathbb{H}=\{\Phi(x):x\in\cal X\}\) 为 Hilbert 空间，且 \(\mathbb{H}\) 上的内积如上；
并且 \(\mathbb{H}\) 具有如下性质，称为再生性质 reproducing property（其实就是定义的衍生物）：

\[\forall h\in \mathbb{H},\forall {x}\in {\cal X},\quad h(x)=\lang h,K(x,\cdot)\rang=\lang h,\Phi(x)\rang \]

从而称 \(\mathbb{H}\) 是关于 \(K\) 的再生核希尔伯特空间 Reproducing kernel Hilbert space (RKHS)，即是我们核方法新的特征空间，尽管它很可能对于一个 \(K\) 并不唯一。这个定理允许我们在处理 \(K(x,y)\) 时，可以将其写成 \(\mathbb{H}\) 上的内积；此外可以在此基础上定义 \(\mathbb{H}\) 上的范数为 \(\Vert h\Vert _{\mathbb{H}}=\sqrt{\lang h,h\rang}\)
总之，有了这个保证，我们寻找特征空间的任务就变为寻找一个合适的 PDS 核

给出一种推导思路：
我们手头只有一个 \(K:\cal X\times X\to\mathbb{R}\) 且暂时不具备任何性质，我们最终的目的是构造出 \(K(x,y)=\lang\Phi(x),\Phi(y)\rang\)，也就是构造一个 \(\Phi\) 并说明 \(\lang\Phi(x),\Phi(y)\rang\triangleq K(x,y)\) 是 \(\{\Phi\}\) 上的内积，因此需要为其引入一些条件（其实就是之前提到的 PDS）
首先令 \(K(\cdot,\cdot)\) 满足对称性，然后拆成一项关于另一项的函数 \(K(x,y)=\Phi(x)(y)=\Phi(y)(x)\)，现在我们希望这个 \(\Phi:\cal X\to\mathbb{R}\) 就是我们想要的
为了证明 \(\lang\Phi(x),\Phi(y)\rang\) 是 \(\mathbb{H}=\{\Phi(x):x\in{\cal X}\}\) 上的内积，我们还要说明它具有双线性和正定性；双线性，即 \(\lang\sum \alpha _i \Phi(x _i),\Phi(y)\rang\)，由于目前 \(\mathbb{H}\) 对线性运算不保证封闭，该式缺少定义，所以我们可以直接赋予其双线性
构造线性空间 \(\mathbb{H} _0\supe\mathbb{H}\)，为 \(\Phi\) 的有限项线性组合：\(\mathbb{H} _0=\{\sum _{i\in I}a _i \Phi(x _i): a _i\in\mathbb{R},x _i\in{\cal X},|I|<\infty \}\)，且具有形式一致的内积
因此，对于 \(f,g\in\mathbb{H} _0\)，\(f=\sum _{i\in I}a _i\Phi(x _i),g=\sum _{j\in J}b _j \Phi(y _j)\)，定义

\[\begin{aligned}\lang f,g\rang &=\lang\sum _{i\in I}a _i\Phi(x _i),\sum _{j\in J}b _j \Phi(y _j)\rang &;\text{回顾：$\lang\Phi(x),\Phi(y)\rang\triangleq K(x,y)$} \\ &\triangleq \sum _{i\in I,j\in J}a _j b _j K(x _i, y _j) &;\text{定义式，人为赋予 $\mathbb{H}$ 双线性} \\ &=\sum _{j\in J} b _j f(y _j)=\sum _{i\in I} a _i g(x _i) &;\text{而 $\mathbb{H} _0$ 继承了对称性和双线性} \end{aligned} \]

对于 \(\mathbb{H _0}\) 上定义的 \(\lang\cdot,\cdot\rang\)，有再生性质 \(\lang f,\Phi(x)\rang=f(x)\) 以及 \(\lang\Phi(x),\Phi(x)\rang=K(x,x)\)，其实都是继承了一开始引入 \(\Phi\) 这个设计后自然而然的结果
现在 \(\mathbb{H _0}\) 上定义的 \(\lang\cdot,\cdot\rang\) 具有对称性和双线性，还差正定性
因此，对任意 \(f\in\mathbb{H} _0\)，应当有 \(\lang f,f\rang=\sum _{i,j\in I}a _i a _j K(x _i, x _j)\ge 0\)，那我们就让它成立，\(K\) 作为 PDS 核的条件就是这么来的
实际上，\(\mathbb{H} _0\) 上的 \(\lang\cdot,\cdot\rang\) 也是 PDS 核，因为 \(\mathbb{H} _0\) 是线性空间，总有 \(\sum _{i,j\in I} c _i c _j\lang f _i, f _j\rang=\lang\sum _{i\in I}c _i f _i,\sum _{j\in I}c _j f _j \rang\ge 0\)；对于 PDS 核，我们推出上面的柯西不等式，可以把它用在 \(\mathbb{H} _0\) 上
为了证明非退化性：\(\lang f,f\rang=0\lrArr f=0\)；解铃还须系铃人，请出再生性质，代入柯西不等式的，得到 \([f(x)] ^2=\lang f,\Phi(x)\rang ^2\le \lang f,f\rang\lang \Phi(x),\Phi(x)\rang=\lang f,f\rang K(x,x)\)，从而若 \(\lang f,f\rang=0\)，则 \(f(x)=0\) 对任意 \(x\) 成立，从而 \(f=0\)，反之亦然
于是 \(\lang\cdot,\cdot\rang\) 是 \(\mathbb{H} _0\) 上的内积
由于 \(\mathbb{H}\sube\mathbb{H} _0\)，为了证明 \(\lang\cdot,\cdot\rang\) 也是 \(\mathbb{H}\) 的内积，只需要证明 \(\mathbb{H} _0\) is dense in \(\mathbb{H}\)，从而再生性质对 \(\mathbb{H}\) 同样适用

Properties of PDS kernels

现在让我们研究一下 PDS 核的性质，尤其是对于某些运算的封闭性，从而帮助我们构造出更复杂的核

规范化 normalization

上文提过，核 \(K\) 规范化 normalization 得到 \(K _\text{norm}\)，定义为

\[\forall{\bf x, y}\in {\cal X},\quad K _\text{norm}({\bf x, y})=\begin{cases} 0 & K({\bf x, x})K({\bf y, y})=0 \\ \frac{K({\bf x, y})}{\sqrt{K({\bf x, x})K({\bf y, y})}} & \text{otherwise}\end{cases} \]

规范化后，有 \(K({\bf x,x})\ne 0\rArr K _\text{norm}({\bf x,x})=1\)；且 \(K _\text{norm}({\bf x,y})\) 为两者的“夹角余弦”
此外有定理：PDS 核规范化后依然是 PDS
证明只需代入定义，写成 \(\mathbb{H}\) 的内积形式，利用一下线性性就行

Empirical kernel map

尽管我们能根据 \(K\) 构造出 \(\mathbb{H}\)，但它还是太抽象了，有些时候我们需要一个确切的特征空间映射 \(\Phi\) 方便处理优化问题
根据 \(K\) 近似求一个 \(\Phi\)，称为 Empirical kernel map，但是先跳过

Closure properties of PDS kernels

Th. Closure properties of PDS kernels
PDS 核 \(K:{\cal X \times X}\to\mathbb{R}\) 对如下运算封闭：加法，乘法，张量乘法 tensor product，序列的逐点收敛 pointwise limit，幂级数
其中

• PDS 核 \(K,K'\) 的张量乘法 \(K\otimes K':{\cal X} ^2\times {\cal X} ^2\to\mathbb{R}\)，定义为（既然称作张量，应该是这么理解的吧）
  \[\forall x _1, x _2, x _1', x _2'\in{\cal X},\quad (K\otimes K')((x _1, x _1'), (x _2, x _2'))=K(x _1, x _2)K'(x _1', x _2') \]

• PDS 核的序列 \((K _n)\) 的逐点收敛 pointwise limit，定义为 \(\lim _{n\to\infty} K _n = K\)
• PDS 核 \(K\) 的幂级数，定义为 \(\sum _{n=0} ^{\infty} a _n K ^n, a _n\ge 0\)

证明
考虑 PDS 核 \(K,K'\) 关于样本的核矩阵 \(\bf K, K'\)，对于任意 \(\bf c\)，有 \({\bf c^\top Kc}\ge 0,{\bf c ^\top K'c}\ge 0\)，则 \({\bf c^\top (K+K')c}\ge 0\)，故加法成立
对任意对称半正定矩阵 SPSD 总能分解为 \(\bf K=MM^\top\)；\(KK'\) 的核矩阵为 \([{\bf K} _{ij}{\bf K'} _{ij}] _{ij}\)，则 \(\sum c _i c _j({\bf K} _{ij}{\bf K'} _{ij})\) 可以写成新的向量 \({\bf z}\) 关于 \(\bf K'\) 的二次型，从而大等于零
易知核 \(((x _1, x _1'), (x _2, x _2'))\mapsto K(x _1, x _2)\) 和 \(((x _1, x _1'), (x _2, x _2'))\mapsto K(x _1', x _2')\) 是 PDS 核，则张量乘为这两个 PDS 核的乘积，从而为 PDS 核
记 PDS 核的序列 \((K _n)\) 逐点收敛于 pointwise limit \(K\)，则有 \({\bf c^\top K c}=\lim _{n\to\infty}{\bf c ^\top K} _n{\bf c}\ge 0\)，故 \(K\) 也为 PDS 核
幂级数即核的乘法、数乘和加法，和正整数数乘显然保留了 PDS，故得（需保证 \(K\) 在该幂级数的收敛半径内）

例如，根据这个定理，取 \(\exp(K)\) 即可展开为幂级数形式（收敛半径为无穷），从而能保留 PDS；由于 \(({\bf x, y})\mapsto \frac{\bf x\cdot y}{\sigma ^2}\) 是 PDS，故 \(({\bf x, y})\mapsto\exp(\frac{\bf x\cdot y}{\sigma ^2})\) 是 PDS，故其规范化后的高斯核也是 PDS

6.3 Kernel-based algorithms - SVM

回到 SVM，把样本看作先通过一遍 \(\Phi\) 映射，然后求解方法与原本相同，最后再将沿途的内积换回核函数
求解关于 \(\boldsymbol{\alpha}\) 的对偶问题，变为：

\[\max _{\boldsymbol{\alpha}} {\cal L}=\max _{\boldsymbol{\alpha}}\left[ \sum _{i=1} ^m \alpha _i - \frac{1}{2}\sum _{i=1} ^m \sum _{j=1} ^m \alpha _i y _i \alpha _j y _j K({\bf x} _i, {\bf x} _j)\right] \\ subject\ to: {\bf 0}\le{\boldsymbol{\alpha}}\le{\bf C}\wedge \Sigma _{i=1} ^{m}\alpha _i y _i = 0 \]

解得 \(\boldsymbol{\alpha}\) 后，原本有 \({\bf w}=\sum _{i=1} ^{m}\alpha _i y _i {\bf x} _i, b=y _{sv} - {\bf w \cdot x} _{sv}\)，现在变为：

\[h({\bf x})=\text{sgn}\left(\sum _{i=1} ^m \alpha _i y _i K({\bf x} _i, {\bf x}) + b\right)\\ b=y _i - \sum _{j=1} ^{m}\alpha _j y _j K({\bf x} _j, {\bf x} _i), \forall i\in[m] \]

此外，还有些领域，比如回归、排名、降维、聚类，都可以类似地使用核方法，我们之后会学到

Representer theorem 表示定理

回顾核方法下的 SVM，我们可以将对偶问题视作关于函数 \(h:\cal X\to\mathbb{R}\) 的优化问题；对很大一类优化问题（如下），它们的解 \(h ^ *\) 都可写作 \(K(x _i,\cdot)\) 的线性组合，称为表示定理

Th. 表示定理
PDS 核 \(K:\cal X\times X\to \mathbb{R}\)，其 RKHS 为 \(\mathbb{H}=\{\Phi(x):{\cal X}\to\mathbb{R}:x\in\cal X\}\)；则对任意单调不降函数 \(G:\mathbb{R\to R}\) 和任意损失函数 \(L:\mathbb{R} ^m \to \mathbb{R}∪\{\infty\}\)，优化问题

\[\underset{h\in\mathbb{H}}{\text{argmin }} F(h)= \underset{h\in\mathbb{H}}{\text{argmin }} G\Big(\Vert h \Vert _{\mathbb{H}}\Big) + L\Big(h(x _1), \dotsb, h(x _m)\Big) \]

总具有一个该形式的解：\(h ^ * = \sum _{i=1} ^m \alpha _i K(x _i, \cdot)\)
进一步地，若 \(G\) 单调升，则该问题的任意解都有该形式

证明
思路：考虑再生性质 \(h(x)=\lang h,K(x,\cdot)\rang=\lang h _{\text{proj to } K},K(x,\cdot)\rang\)，这启发我们考虑将 \(h\) 投影到 \(K\) 张成的空间里，是否仍然是原问题的解；这就是此定理的来由；投影到若干元素张成的空间，从而将解归为这些形式的线性组合，这个想法倒是挺有意思
记 \(\mathbb{H} _1=\text{span}(\{K(x _i,\cdot):i\in [m]\})\)，将 \(\mathbb{H}\) 分解为 \(\mathbb{H} _1\) 和其垂直分量 \(\mathbb{H} _1 ^⊥\)，对 \(\mathbb{H}\) 的元素同理；我们只要证明 \(F(h _1)\le F(h)\) 就证明了上述定理；
由于 \(h(x _i)=\lang h,K(x _i,\cdot)\rang=\lang h _1,K(x _i,\cdot)\rang = h _1(x _i)\)，故 \(L(h _1)=L(h)\)
并且有 \(G(\Vert h _1\Vert _{\mathbb{H}})\le G(\sqrt{\Vert h _1\Vert _{\mathbb{H}} ^2 + \Vert h ^⊥\Vert _{\mathbb{H}} ^2})=G(\Vert h\Vert _{\mathbb{H}})\)，故得证
若 \(G\) 单调增，则若 \(h ^ *\notin \mathbb{H} _1\)，则有 \(\Vert h ^⊥\Vert _{\mathbb{H}}> 0\)，于是 \(F(h _1 ^*)< F (h ^*)\)，\(h ^ *\) 不会是解；故也得证

Learning guarantees

回到假设，引入 PDS 核 \(K\) 和对应的 RKHS \(\mathbb{H}\) 和 \(\Phi\) 这些概念，发现假设 \(h:{\cal X}\to\mathbb{R}\) 属于 \(\mathbb{H}\)，且有 \(x\mapsto h(x)=\lang h,\Phi(x)\rang\)
考虑有界情况：\({\cal H}=\{h\in\mathbb{H}:\Vert h\Vert _{\mathbb{H}}\le\Lambda \},\Lambda \ge 0\)：

Th. Rademacher complexity of kernel-based hypotheses
在上述情况下，对于样本 \(S\sube\{x:K(x,x)\le r ^2\}\)，有

\[\widehat{\frak{R}} _S({\cal H})\le \frac{\Lambda\sqrt{\text{Tr}[{\bf K}]}}{m}\le \sqrt{\frac{r ^2\Lambda ^2}{m}} \]

证明，原式 \(=\frac{1}{m}\mathbb{E} _{\boldsymbol{\sigma}}[\sup _{\Vert {\bf w}\Vert \le\Lambda}\lang {\bf w},\sum _{i=1} ^{m}\sigma _i \Phi(x _i) \rang]\)，之后就和原来一样

可见核矩阵的迹 \(\text{Tr}(\bf K)\) 对上界很重要；这个定理表明，只要我们有一个合适的核（满足上述限制，而且核矩阵的迹尽量小），我们就能有效地将 \(\widehat{\frak{R}} _S({\cal H})\) 用此上界限住
例如，我们有如下定理：

Th. Margin bound for kernel-based hypotheses
对于样本集 \(\cal X\)，取 PDS 核 \(K:\cal X\times X\to\mathbb{R}\) 使得 \(r ^2=\sup _{x\in\cal X}K(x,x)<\infty\)，对应有 \(\mathbb{H}\) 和 \(\Phi:\cal X\to\mathbb{H}\)
取假设集合 \({\cal H}=\{x\mapsto{\bf w}\cdot\Phi(x):\Vert{\bf w}\Vert _{\mathbb{H}}\le\Lambda\},\Lambda\ge 0\)；则：
固定 \(\rho>0\)，则以至少 \(1-\delta\) 的概率，对任意 \(h\in\cal H\)，有

\[\begin{aligned} R(h)&\le \widehat{R} _{S,\rho}(h) + 2\sqrt{\frac{r ^2\Lambda ^2/\rho ^2}{m}} +\sqrt{\frac{\log \frac{1}{\delta}}{2m}} \\ R(h)&\le \widehat{R} _{S,\rho}(h) + 2\frac{\sqrt{\text{Tr}[{\bf K}]\Lambda ^2/\rho ^2}}{m} +3\sqrt{\frac{\log \frac{2}{\delta}}{2m}} \end{aligned} \]

6.4 Negative definite symmetric kernels

类似搞一个内积，现在我们想用核方法整一个度量 metric，也就是映射 \(K\) 使得 \(K(x,y)=\Vert \Phi(x)-\Phi(y)\Vert ^2\)，该怎么做呢？
很自然地，我们可以先利用 PDS 核造一个：对于 PDS 核 \(K'\) 与对应的 \(\Phi,\mathbb{H}\)，令：

\[K(x,y)\triangleq\Vert \Phi(x)-\Phi(y)\Vert ^2=K'(x,x)+K'(y,y)-2K'(x,y) \]

此时我们研究一下 \(K\) 的性质，对任意样本 \(S=(x _1,\dotsb,x _m)\) 和 \({\bf c}\in \mathbb{R} ^{m\times 1}\)，有：

\[\begin{aligned} {\bf c ^\top K c} &= \sum _{i=1} ^m \sum _{j=1} ^m c _i c _j K(x _i, x _j) \\ &= 2\sum _{i=1} ^m c _i K'(x _i, x _i) \sum _{j=1} ^m c _j - 2\sum _{i=1} ^m \sum _{j=1} ^m c _i c _j K'(x _i, x _j) \\ &= -2\sum _{i=1} ^m \sum _{j=1} ^m c _i c _j K'(x _i, x _j) \le 0 \qquad;\text{令 $\sum _{i=1} ^m c _i=0$} \end{aligned} \]

由此，我们定义 negative definite symmetric (NDS) kernel，为：

Def. Negative definite symmetric (NDS) kernels
称映射 \(K:\cal X\times X\to\mathbb{R}\) 为负定对称核 NDS，若它满足对称性，且对任意 \(S=(x _1,\dotsb,x _m)\sube \cal X\) 和 \({\bf c}\in \mathbb{R} ^{m\times 1},{\bf 1 ^\top c}=0\)，有：

\[{\bf c ^\top K c}\le 0 \]

例如，\((x,y)\mapsto\Vert x-y\Vert ^2\) 就是一个 NDS 核；实际上，它对应最简单的恒等映射 \(\Phi:x\mapsto x\)

由上，我们只要有一个 PDS 核 \(K'\)，就能构造出一个 NDS 核 \(K\)（事实上 \(-K'\) 就是 NDS 核，但是 \(-K\) 不一定是 PDS 核）；那么能否通过 NDS 核构造 PDS 核、从而存在一个 metric 呢？
更具体地考虑：\(2{\bf xy}=\Vert{\bf x}\Vert ^2+\Vert{\bf y}\Vert ^2 -\Vert {\bf x-y}\Vert ^2\)，后者只有 \(\Vert {\bf x-y}\Vert ^2\) 符合度量形式，我们可以考虑参考一个固定点 \(\bf z\)，变为 \(2{\bf (x-z)(y-z)}=\Vert{\bf x-z}\Vert ^2+\Vert{\bf y-z}\Vert ^2 -\Vert {\bf x-y}\Vert ^2\)，也就构造出了 PDS 核
所以，固定任意 \(z\in\cal X\)，可令 \(K'\) 为：

\[K'(x,y)\triangleq \frac{1}{2}\Big[ K(x,z) + K(y, z)-K(x,y) \Big] \]

之后的定理会用到它；受其启发，有如下定理：

Th. PDS ↔ NDS
映射 \(K,K':\cal X\times X\to \mathbb{R}\)，固定任意 \(z\in\cal X\)，若有：

\[K'(x,y)= K(x,z) + K(y, z)-K(x,y)-K(z,z) \]

则 \(K\) 是 NDS 核，等价于 \(K'\) 是 PDS 核

和上述式子比起来，去掉系数保持 PDS 性可以理解，那为什么会多了个似乎总是为零的项 \(-K(z,z)\) 呢？口胡，从逻辑顺序来说，NDS 的定义里其实不包含 \(K(z,z)=0\)，但我们从具体的内积考虑时却暗示了它成立，因此两者并不是完全能够类比的；例如，前者代入 \(\bf z,y\) 有 \({\bf (z-z)(y-z)}=0\)，而后者代入为 \(K'(z,y)=K(z,z)\)；因此为了形式上统一以及证明需要，我们添加 \(-K(z,z)\) 项

证明
后推前易证，现在考虑前推后
首先注意到 \(K'(x,z)=0\)，这就是为什么要式子最后要减一个 \(K(z,z)\)
记 \(c _0=-{\bf 1 ^\top c}\)，则 \(\sum _{i=0} ^m c _i = 0\)（似乎是个小套路），对固定的 \(x _0=z\)，样本 \((x _0, x _1,\dotsb, x _m)\)，有 \(\sum _{i,j=0} ^{m}c _i c _j K(x _i, x _j)\le 0\)，展开：

\[\begin{aligned}\sum _{i=0} ^m \sum _{j=0} ^{m}c _i c _j K(x _i, x _j) &= \sum _{i=0} ^m \sum _{j=0} ^{m}c _i c _j[K(x _i, x _0) + K(x _j, x _0) - K(x _0, x _0) - K'(x _i, x _j)] \\ &= -\sum _{i=0} ^m \sum _{j=0} ^m c _i c _j K'(x _i, x _j) \\ &= -\sum _{i=1} ^m \sum _{j=1} ^m c _i c _j K'(x _i, x _j) -2 c _0\sum _{i=0} ^m c _i K'(x _i, x _0) + c _0 ^2 K'(x _0, x _0) \\ &= -\sum _{i=1} ^m \sum _{j=1} ^m c _i c _j K'(x _i, x _j) \qquad ;K(x,x _0)\equiv0 \\ &\le 0 \end{aligned}\]

由式子的最后两行，定理得证

因此，NDS 核都对应存在一个映射到 Hilbert 空间的度量，用定理描述为：

Th. Metric for NDS kernels
NDS 核 \(K\)，且满足非退化性 \(K(x,y)=0\lrArr x=y\)，则存在一个 Hilbert 空间 \(\mathbb{H}\) 和映射 \(\Phi:\cal X\to\mathbb{H}\)，使得

\[\forall x,y\in{\cal X},\quad K(x,y)=\Vert \Phi(x)-\Phi(y)\Vert ^2 \]

此时 \(\sqrt{K}\) 就是一个 metric

证明
取 \(K'(x,y)\triangleq \frac{1}{2}[ K(x,z) + K(y, z)-K(x,y)]\)，由 \(K(z,z)\equiv 0\) 和上文定理知 \(K'\) 为 PDS 核，于是取其 \(\mathbb{H},\Phi\)，则 \(\Vert \Phi(x)-\Phi(y)\Vert ^2=K'(x,x)+K'(y,y)-2K'(x,y)\)，代入后 \(=K(x,y)\)，得证

---

附：关于希尔伯特空间和 RKHS

https://zhuanlan.zhihu.com/p/527182282

希尔伯特空间 := 线性空间，且定义内积 \(\to\) 范数 \(\to\) 距离 \(\to\) 完备

空间即集合，且具有某些结构/性质

• 距离，具有该定义称为度量空间
  定义为映射 \(d:{\cal X\times X}\to \mathbb{R}\)，满足
  • 正定性：\(d(x, y)\ge 0\)，且 \(d(x,y)=0\lrArr x=y\)
  • 对称性：\(d(x,y)=d(y,x)\)
  • 三角不等式：\(d(x,y)\le d(x, z)+d(z, y)\)
• 向量，具有该性质称为向量空间（线性空间）
  若其元素（称为向量）对加法和数乘满足
  • 加法交换律：\(\vec{x}+\vec{y} = \vec{y}+\vec{x}\)
  • 加法结合律：\((\vec{x}+\vec{y})+\vec{z}=\vec{x}+(\vec{y}+\vec{z})\)
  • 向量单位元：存在唯一的 \(\vec{0}\) 使得 \(\vec{x}+\vec{0}=\vec{x}\)
  • 加法逆元：存在唯一的 \(-\vec{x}\) 使得 \(\vec{x}+(-\vec{x})=\vec{0}\)
  • 向量分配律：\((\alpha + \beta)\vec{x} = \alpha \vec{x} + \beta \vec{x}\)
  • 标量分配律：\(\alpha(\vec{x} + \vec{y}) = \alpha \vec{x} + \alpha \vec{y}\)
  • 结合律：\((\alpha \beta)\vec{x} = \alpha(\beta \vec{x})\)
  • 标量单位元：\(1\cdot \vec{x} = \vec{x}\)
• 范数，具有该定义的线性空间称为线性赋范空间
  定义为映射 \(\Vert\cdot\Vert:{\cal X}\to \mathbb{R}\)，满足
  • 正定性：\(\Vert \vec{x}\Vert\ge 0\)，且 \(\Vert \vec{x}\Vert=0\lrArr \vec{x}=\vec{0}\)
  • 齐次性：\(\Vert\alpha \vec{x}\Vert=\Vert \alpha\Vert\Vert \vec{x}\Vert\)
  • 三角不等式：\(\Vert \vec{x}+\vec{y}\Vert\le \Vert \vec{x}\Vert+\Vert \vec{y}\Vert\)
• 内积，具有该定义的向量空间称为内积空间
  定义为映射 \(\lang\cdot,\cdot\rang:{\cal X\times X}\to \mathbb{C}\)，满足
  • 正定性：\(\lang \vec x, \vec x \rang \ge 0\)，且 \(\lang \vec x,\vec x \rang = 0 \Leftrightarrow \vec x=\vec 0\)
  • 线性：\(\lang \alpha \vec x+ \beta \vec y,\vec z\rang = \alpha \lang \vec x, \vec z \rang +\beta \lang\vec y,\vec z \rang\)
  • 共轭线性：\(\lang \vec z, \alpha \vec x+ \beta \vec y\rang = \bar\alpha \lang \vec z, \vec x \rang +\bar\beta \lang \vec z, \vec y \rang\)，由线性+共轭对称推出，与线性共称为双线性
  • 共轭对称：\(\lang \vec x, \vec y \rang = \overline{\lang \vec y, \vec x \rang}\)
• 完备性，具有该性质的度量空间称为完备度量空间
  定义为任意柯西列的极限仍然在这个空间中
  • 柯西列为这个空间的元素构成的序列 \(\{x _n\}\)，满足在无穷远处两个元素之间的距离趋于零 \(\lim _{n,m\to\infty}d(x _n, x _m)=0\)
  • 感性理解，即该集合内部、边界不缺点，柯西序列只是提供了一种逼近的刻画方式
• 巴拿赫空间
  若用范数定义距离 \(d(x,y)=\Vert x-y\Vert\)，且在该距离下完备
• 希尔伯特空间
  若用内积定义范数 \(\Vert x\Vert=\sqrt{\lang x, x\rang}\)，且在该范数下的赋范线性空间是巴拿赫空间

再生核希尔伯特空间
称一个希尔伯特空间是再生核希尔伯特空间 \(\mathbb{H}\)，若：

• 该希尔伯特空间 \(\mathbb{H}\) 由定义在集合 \(\cal X\) 上的所有实值函数组成 \(\mathbb{H}=\{ h:{\cal X}\to \mathbb{R}\}\)
• 在该希尔伯特空间 \(\mathbb{H}\) 上，对任意 \(x\in\cal X\)，定义泛函 \(L _x(h)=h(x),h\in \mathbb{H}\)，则满足该泛函连续（回顾：连续 \(\larr\) 收敛 \(\larr\) 距离）

该定义之所以称为“再生核”，是因为满足性质：

Th. “再生 Reproducing”
在再生希尔伯特空间 \(\mathbb{H}\) 上，对于任意 \(x\in\cal X\)，定义泛函 \(L _x(h)=h(x),h\in \mathbb{H}\)，根据里斯定理，存在唯一的 \(K _x\in\mathbb{H}\)，使得 \(h(x)=L _x(h)=\lang h, K _x\rang\)
也就是说，\(h(x)\) 可由 \(h\) 和 \(K _x\) “再生”

进一步地，对于 \(x, y\) 和对应的 \(K _x, K _y\)，有 \(K _x(y)=K _y(x)=\lang K _x, K _y\rang\)，故可定义核函数 \(K(x, y)=\lang K _x, K _y\rang\)，该核函数为 PDS 核