【笔记】近世代数 - 群的同态基本定理
近世代数学的那些东西，感觉挺有意思，说不定以后有点用
这里非常挑剔（懒）地选了一小部分
群
非空集合 \(G\)
定义在 \(G\) 上的一个二元代数运算 \(\circ\) 是一个映射 \(G\times G\to G\)
称 \(G\) 对它的乘法运算 \(\circ\) 构成一个群 (group)，当且仅当：
- \(\circ\) 满足结合律（从而是半群）
- 存在单位元 \(e\)（从而是幺半群）
- \(G\) 中任意元素都存在逆元
记作群 \((G, \circ)\)
子群
群 \(G\) 的非空子集 \(S\) 称为 \(G\) 的子群，若 \(S\) 对 \(\circ\) 也构成一个群，又即 \(S\) 对 \(\circ\) 封闭，又即 \(SS=S\)
子群陪集
设 \(H\) 是群 \(G\) 的子群，\(a\) 为 \(G\) 任一元素
集合 \(aH\) 称为子群 \(H\) 的一个左陪集（同理有右陪集，两者定理相同）
Th1. \(aH=H\iff a\in H\)
Th2. \(aH=bH\iff a^{-1}b\in H\)
Th3. \(\forall a,b\in G, aH=bH\ or\ aH\cap bH=\emptyset\)
Th4. \(\forall a,b\in G, |aH|=|bH|\)
可见可以根据子群 \(H\) 的陪集对 \(G\) 做一个划分
根据这个对 \(G\) 的划分，可以定义等价关系 \(\cong\)：
\(a\cong b\iff aH=bH \iff ab^{-1}\in H\)
Th5. 拉格朗日，Lagrange
有限群 \(G\) 的阶为 \(N\)，\(H\) 是 \(G\) 的一个 \(n\) 阶子群，则：\(N=n\cdot [G:H]\)
\([G:H]\) 称为 \(H\) 在 \(G\) 中的指数，等于 \(H\) 的所有不同的左陪集的个数
推论：有限群每个元素的阶都能整除该有限群的阶；有限群的阶是质数→其为循环群
正规子群
设 \(H\) 是群 \(G\) 的子群，称 \(H\) 为 \(G\) 的正规子群，若
\(\forall a\in G, aH=Ha\)
Th6. 正规子群 \(H\) 的所有左陪集构成集族 \(S_l\) 对群子集乘法构成一个群
群子集乘法：\(AB=\lbrace a\circ b|a\in A, b\in B\rbrace\)
商群：正规子群 \(H\) 的所有左陪集构成集族 \(S_l\) 对群子集乘法构成的群，记为 \(G/H\)
上述定义得到的等价关系 \(\cong\)，此时也是同余关系
同余关系：\(a\cong a', b\cong b'\implies a\circ b = a'\circ b'\)，又即“对乘法不变”
于是我们也可以这么理解定理 6：
Th7. 设 \(\cong\) 对应的划分 \(\psi\)，元素 \(x\) 所在类 \([x]\)，在 \(\psi\) 上定义乘法：
\([x][y]=[x\circ y]\)
则其是 \(\psi\) 上的二元代数运算，且 \([e]=eH=H\)
同态基本定理
同态：设群 \((G, \circ), (G', \cdot)\)，若存在一个映射 \(\phi:G\to G'\)，满足：
\(\forall a,b\in G, \phi(a\circ b)=\phi(a)\cdot \phi(b)\)
则称 \(\phi\) 是一个 \(G\) 到 \(G'\) 的同态，从而称 \(G\) 和 \(G'\) 同态
若 \(\phi\) 是满射，则称 \(\phi\) 是满同态，记为 \(G\backsim G'\)，以下我们都认为是满同态
当 \(\phi\) 为一一对应时，称为同构，记为 \(G\cong G'\)
满同态具有几个性质：
Th8. \(\phi(a^{-1})=[\phi(a)]^{-1}, \phi(e)=e'\)
Th9. 若 \(H\) 是 \(G\) 的（正规）子群，则 \(\phi(H)\) 是 \(G'\) 的（正规）子群
Th10. 若 \(H'\) 是 \(G'\) 的（正规）子群，则 \(\phi^{-1}(H')\) 是 \(G\) 的（正规）子群
同时考虑上述的商群概念 \(G/H\)，可知 \(G\backsim G/H\)，记该同态为 \(\gamma\)，称为自然同态，即有
\(\gamma(a)=aH\)，且 \([a\circ b]=\gamma(a\circ b)=\gamma(a)\gamma(b)=[a][b]\)
接下来给出正规子群与同态的又一个关系：
Th11. 设 \(G\backsim G'\)，则 \(\phi^{-1}(e')\) 是 \(G\) 的正规子群，记为 \(Ker\ \phi\)，称为同态 \(\phi\) 的核
Th12. 群的同态基本定理
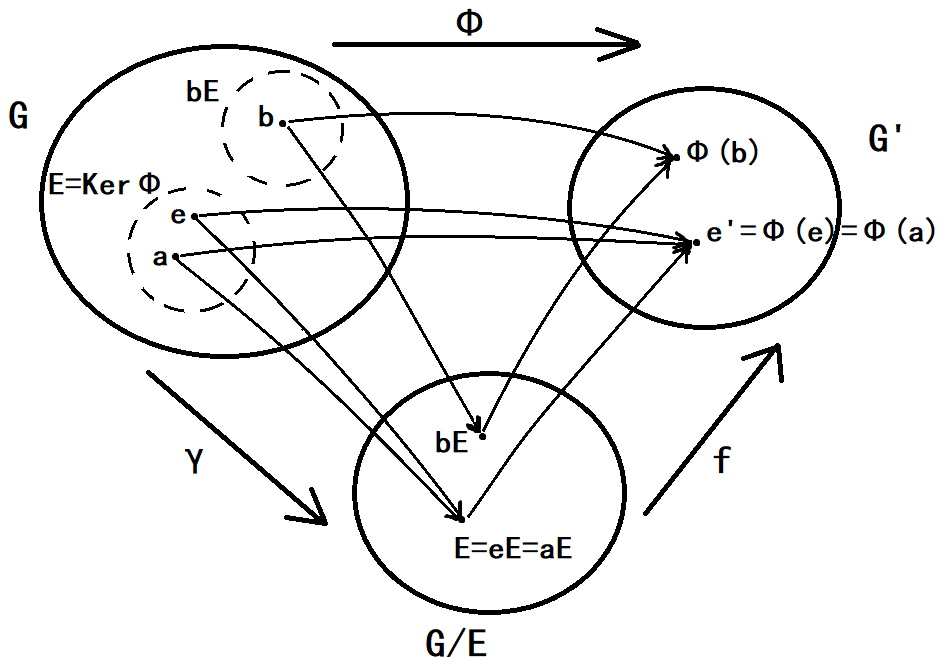
设 \(\phi\) 是群 \(G\) 到 \(G'\) 的满同态，\(E=Ker\ \phi\)，则 \(G/E\cong G'\)
于是群 \(G\) 的任一满同态 \(\phi\) 都可分解称一个自然同态 \(\gamma\) 和一个同构 \(f\) 的合成，即 \(\phi=\gamma\circ f\)
