【题解】Codeforces Round #767 (Div. 2 + Div. 1 E)

D

只需注意到对于一个符合题意的回文串，当两侧的两个字符串长为2和3时，也可以拿来组成一个新的回文串
让人场上懵逼25分钟不知道WA在什么地方最后爆炸的原因是——
hash弄了个零！h = h*26+(s[i]-'a') 是错的！不能有零！！！前导零在哈希里是体现不出来的！！！
赛后才反应过来...感觉降智..

E

方向：考虑选一些格子，其异或和即为所有格子的异或和
考虑每个格子如何被贡献？与其相邻的格子被选中了奇数个
于是问题等价于，构造一种格子的选法，使得每个格子相邻的格子被选了奇数个
画图找规律（从上到下一行一行地考虑，首先(1, 2)肯定有，从左往右..）：

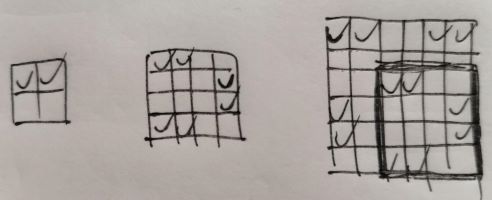
发现6X6里有个4X4，顺着往外扩圈的思路想：

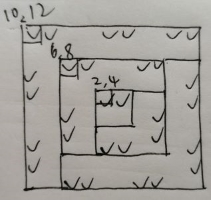
F1, F2

我们很容易可以想到一个状态：设 f[i][j] 表示前 i 轮，有 j 次add的最小得分
那么有 f[i][j] = min{f[i-1][j-1]+x, f[i-1][j]-x}，x是Alice根据当前的状态(i,j)选择的，且满足x属于[0, k]，并使等式右边尽量大
可以想到两个特殊情况：若 f[i-1][j-1]>f[i-1][j]，x取0；若两者之差超过2k，x最多也只能取到k...而且在模意义下还有判断大小...
我们猜测或者其他什么方式，假设上面两个情况不存在，即 \(0\leq f[i][j]-f[i][j-1]\leq 2k\) 恒成立，则将会有递推式：
\(f[i][j] = (f[i-1][j-1] + f[i-1][j]) / 2\)
且 \(f[i][0] = 0, f[i][i] = iK\)（为方便写，以下直接省略K）
那么我们数学归纳法地证明这个性质：假设对于 a < b < c，满足相邻之差小等于 2，容易得到 (a+b)/2 < (b+c)/2 也满足之差小等于 2
此外还要证明 \(f[i][i]-f[i][i-1]\leq 2\)，且 f[i][i] = i，即证 f[i][i-1] >= i-2；考虑其实际意义，只需Alice所有回合都取K，此时的答案就是(i-1-1=)i-2

接下来考虑方程式怎么O(n)处理，即（这一类类似杨辉三角的东西）：
\(f[i][j] = (f[i-1][j-1] + f[i-1][j]) / 2\)，且 \(f[i][0] = 0, f[i][i] = i\)
方法就是直接考虑每个 f[i][i] 的贡献，(i, i) 到达 (n, m) 的所有可能路径数就是贡献的倍数，即 \(C_{n-i-1}^{m-i}\)，（第一次只能向下走）

div1 E

考虑最大边，其两端的两个联通块，若其一连通块内有open的，则另一个联通块内的所有点的答案就是这个最大边权，若无，则递归为两个连通块内各自的子问题
可以考虑对每一条边都建一个点，左右儿子分别对应两个连通块；叶子节点为原有节点；注意这是一个二叉树
这样我们建的树就刻画了 以边权大小 的这种“可达性”的连通块题，实际建树时可以用并查集（其实以前见过这类建树...不过是以点权大小考虑的
接着我们考虑一个open节点对一个询问节点的贡献：我们发现答案即为两者的lca（代表的边的边权）
那么对于多个open节点对一个询问节点的贡献，就是所有点的lca
我们怎么快速求多个节点的lca呢？注意到这是一个二叉树，我们考虑其中序遍历，那么多个节点的lca，就是中序遍历序号最小和最大的两个节点的lca！
那么我们只需要维护序号最小和最大的两个节点就行了，上线段树
图示和代码：

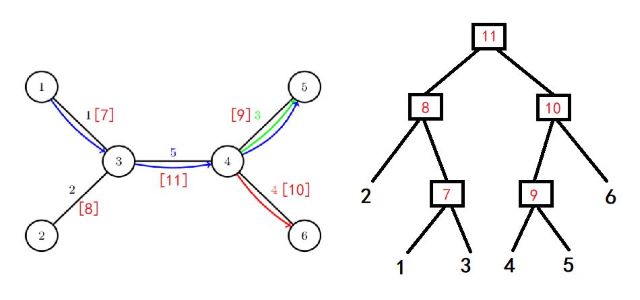
// coding: 23:17 ~ 00:24(ac)
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 1500006;
int N, Q, fst[MAXN];
int fa[MAXN];
int tot, W[MAXN], ls[MAXN], rs[MAXN], id[MAXN], S[MAXN];
int dp[MAXN][20], lg[MAXN], dep[MAXN];
int clk;
struct edge {
	int v, w, pre;
} e[MAXN];
struct Edge {
	int u, v, w;
} P[MAXN];
int cmp(Edge x, Edge y) { return x.w < y.w; }
struct segmentTree {
	#define lson (x<<1)
	#define rson (x<<1|1)
	int left[MAXN], right[MAXN];
	int tmpl[MAXN], tmpr[MAXN], tag[MAXN];
	void pushup(int x) {
		tmpl[x] = min(tmpl[lson], tmpl[rson]);
		tmpr[x] = max(tmpr[lson], tmpr[rson]);
	}
	void pushdown(int x) {
		if (tag[x]==0) {
			tmpl[lson] = tmpl[rson] = tot+1;
			tmpr[lson] = tmpr[rson] = 0;
			tag[lson] = tag[rson] = 0, tag[x] = -1;
		} else if (tag[x]==1) {
			tmpl[lson] = left[lson], tmpr[lson] = right[lson];
			tmpl[rson] = left[rson], tmpr[rson] = right[rson];
			tag[lson] = tag[rson] = 1, tag[x] = -1;
		}
	}
	void build(int x, int l, int r) {
		tmpl[x] = tot+1, tmpr[x] = 0, tag[x] = -1;
		if (l==r) left[x] = right[x] = id[l];
		else {
			int mid = (l + r) >> 1;
			build(lson, l, mid), build(rson, mid+1, r);
			left[x] = min(left[lson], left[rson]);
			right[x] = max(right[lson], right[rson]);
		}
	}
	void update(int x, int l, int r, int _l, int _r, int t) {
		if (l>=_l && r<=_r) {
			if (t==0) tmpl[x] = tot+1, tmpr[x] = 0, tag[x] = 0;
			else tmpl[x] = left[x], tmpr[x] = right[x], tag[x] = 1;
		} else {
			pushdown(x);
			int mid = (l + r) >> 1;
			if (mid>=_l) update(lson, l, mid, _l, _r, t);
			if (mid< _r) update(rson, mid+1, r, _l, _r, t);
			pushup(x);
		}
	}
} ST;
void adde(int a, int b, int c, int k)
{
	e[k].v = b, e[k].w = c, e[k].pre = fst[a], fst[a] = k;
}
int find(int x) { return fa[x]==x ? x : fa[x]=find(fa[x]); }
void init(int x, int d)
{
//	printf("[%d, w=%d] -> (%d, %d)\n", x, W[x], ls[x], rs[x]);
	dep[x] = d;
	for (int o=1; o<=lg[d]; o++) dp[x][o] = dp[dp[x][o-1]][o-1];
	if (ls[x]) dp[ls[x]][0] = x, init(ls[x], d+1);
	S[++clk] = x, id[x] = clk;
	if (rs[x]) dp[rs[x]][0] = x, init(rs[x], d+1);
}
int lca(int a, int b)
{
	if (dep[a] < dep[b]) a ^= b ^= a ^= b;
	while (dep[a] > dep[b]) a = dp[a][lg[dep[a]-dep[b]]];
	if (a == b) return a;
	for (int i=lg[dep[a]]; i>=0; i--)
		if (dp[a][i] != dp[b][i]) a = dp[a][i], b = dp[b][i];
	return dp[a][0];
}
int main()
{
	scanf("%d%d", &N, &Q);
	for (int i=1; i< N; i++) {
		int a, b, c; scanf("%d%d%d", &a, &b, &c);
		adde(a, b, c, i), adde(b, a, c, i+N);
		P[i].u = a, P[i].v = b, P[i].w = c;
	}
	sort(P+1, P+N, cmp), tot = N;
	for (int i=1; i<=N; i++) fa[i] = i;
	for (int i=1; i< N; i++) {
		int u = P[i].u, v = P[i].v, w = P[i].w;
		int fu = find(u), fv = find(v);
		++tot, fa[tot] = tot, ls[tot] = fu, rs[tot] = fv, W[tot] = w;
		fa[fu] = tot, fa[fv] = tot;
	}
	
	for (int i=0; i< MAXN; i++) lg[i] = lg[i-1] + ((1<<(lg[i-1]+1))==i);
	init(tot, 0), ST.build(1, 1, N);
//	for (int i=1; i<=tot; i++) printf("%d ", S[i]); puts("");
//	for (int i=1; i<=N; i++) printf("id[%d] = %d\n", i, id[i]);
	
	for (; Q; Q--) {
		int opt; scanf("%d", &opt);
		if (opt==1) {
			int l, r; scanf("%d%d", &l, &r);
			ST.update(1, 1, N, l, r, 1);
		} else if (opt==2) {
			int l, r; scanf("%d%d", &l, &r);
			ST.update(1, 1, N, l, r, 0);
		} else {
			int x; scanf("%d", &x);
			int l = ST.tmpl[1], r = ST.tmpr[1];
			if (l> r) puts("-1");
			else {
				int c = lca(S[l], S[r]);
				if (c==x) puts("-1"); else printf("%d\n", W[lca(x, c)]);
			}
		}
	//	printf("(%d, %d)\n", ST.tmpl[1], ST.tmpr[1]);
	}
}