【题解】Educational Codeforces Round 121 (Rated for Div. 2)

C

栈

D

这我实在是憨憨...先是想了很多没用的东西，一点方向性都没有...
考虑枚举，哪个少就枚举哪个。所以哪个少？2 的幂。

E

挺有趣的才怪，不知道是不是做烦了
UPD：就是做烦了，草正解好漂亮，见底下

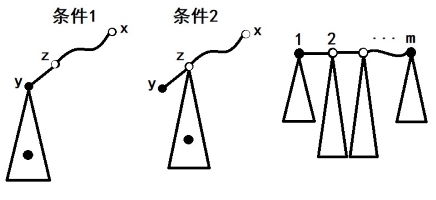
初步思考得到，白点 x 能到达黑点 y，需要满足两种条件之一：一是 y 的身后还有黑点，二是 x 往 y 的路径上的倒数第一个节点 z 的子树上（包括 z）有黑点，称之为条件 1 和条件 2（当然还要注意到 x 和 y 邻接的情况）
但是就这样还是找不到“方向性”，所以我们考虑选定一个参考，方便转化成有根树的问题
我们选取图上两个黑点之间的路径，得到如图的形式，（可以通过dfs+栈，所以之间的所有点都是白点），这里编号 1...m，称为节点 1...m，对应子树称为子树 1...m
我们接下来（胡乱）寻找一些性质：

1. 对于所有子树，内部的节点可以不断向上走到根，所以子树 1 和 m 内的所有节点已经有解；若节点 i（以下一般默认 1<i<m）有解，则其子树内节点有解
2. 若节点 i 的子树内有黑点，则节点 2...m-1（及其子树）都能走到 i
3. 若子树 1 和 m 内（不包括节点 1 和 m）有黑点，则所有点都有解
4. 若节点 i 能走到其子树内的某个黑点，则所有点都有解
5. 若节点 i 能走到其子树内的某个黑点，当且仅当节点 i 的某个儿子就是黑点，或者其子树内满足条件 1 或条件 2（含义见上）
6. 节点 2 和 m-1 有解
7. （上面我们考虑的是所有节点都有解的情况，这里考虑每个黑点各自的贡献）对于子树 2...m-1 内的某个黑点，以其父节点为根的子树内所有点都有解（此外若还有从更上方走来的节点，则需满足条件 1 或 2，上面已经讨论过）
8. 注意，我们还需要想到节点 1 和 m 的贡献，结合条件 2，即子树 2 或 m-1 内有黑点，此时所有点都有解（这条是我WA出来的...）

综上我们就可以做题了。
首先拉出一条链（dfs0），然后判断上面性质中所有可以使所有点都有解的条件：编号3（dfs1），编号5、8（dfs2）；然后单独做每个黑点的贡献：编号 6、7（dfs3）
代码：

#include <cstdio>
using namespace std;
const int MAXN = 300005;
int N, C[MAXN], fst[MAXN];
int stk[MAXN], top, f[MAXN], all;
int ansn[MAXN];
struct edge {
	int v, pre;
} e[MAXN<<1];
void adde(int a, int b, int k)
{
	e[k].v = b, e[k].pre = fst[a], fst[a] = k;
}
int dfs0(int x, int fa)
{
	for (int o=fst[x]; o; o=e[o].pre) if (e[o].v!=fa) {
		stk[++top] = e[o].v;
		if (C[e[o].v] || dfs0(e[o].v, x)) return 1;
		top--;
	}
	return 0;
}
int dfs1(int x, int fa)
{
	for (int o=fst[x]; o; o=e[o].pre) if (e[o].v!=fa)
		if (C[e[o].v] || dfs1(e[o].v, x)) return 1;
	return 0;
}
void dfs2(int x, int fa)
{
	if (C[x]) f[x] = 1;
	int cntf = 0, cntc = 0;
	for (int o=fst[x]; o; o=e[o].pre) if (e[o].v!=fa) {
		dfs2(e[o].v, x), f[x] |= f[e[o].v];
		if (C[x] && f[e[o].v]) all = 1;
		if (C[e[o].v]) cntc++;
		if (f[e[o].v]) cntf++;
	}
	if (cntc && cntf> 1) all = 1;
	if (f[x] && (fa==stk[2]||fa==stk[top-1])) all = 1;
}
void dfs3(int x, int fa, int c)
{
	if (C[x]) c = 1;
	for (int o=fst[x]; o; o=e[o].pre) if (e[o].v!=fa) c |= C[e[o].v];
	ansn[x] |= c;
	for (int o=fst[x]; o; o=e[o].pre) if (e[o].v!=fa) dfs3(e[o].v, x, c);
}
int main()
{
	scanf("%d", &N);
	for (int i=1; i<=N; i++) scanf("%d", &C[i]);
	for (int i=1; i< N; i++) {
		int a, b; scanf("%d%d", &a, &b);
		adde(a, b, i), adde(b, a, i+N);
	}
	for (int i=1; i<=N; i++) if (C[i]) {
		stk[top=1] = i, dfs0(i, 0); break;
	}
//	for (int i=1; i<=top; i++) printf("%d, ", stk[i]); puts("");
	if (dfs1(stk[1], stk[2]) || dfs1(stk[top], stk[top-1])) all = 1;
	for (int i=2; i< top; i++) {
		int x = stk[i];
		if (C[x]) all = 1;
		for (int o=fst[x]; o; o=e[o].pre)
			if (e[o].v!=stk[i-1] && e[o].v!=stk[i+1] && C[e[o].v]) all=1;
	}
	for (int i=2; i< top; i++) {
		int x = stk[i];
		for (int o=fst[x]; o; o=e[o].pre)
			if (e[o].v!=stk[i-1] && e[o].v!=stk[i+1]) dfs2(e[o].v, x);
	}
	// print black
	dfs3(stk[1], stk[2], 1), dfs3(stk[top], stk[top-1], 1);
	for (int i=2; i< top; i++) {
		int x = stk[i], c = (i==2)||(i==top-1);
		ansn[x] |= c;
		for (int o=fst[x]; o; o=e[o].pre)
			if (e[o].v!=stk[i-1] && e[o].v!=stk[i+1]) dfs3(e[o].v, x, c);
	}
	if (all) for (int i=1; i<=N; i++) ansn[i] = 1;
	for (int i=1; i<=N; i++) printf("%d ", ansn[i]);
}

好了这里是正解，我们考虑对于通过边 x→y，若下一步不用返回的条件是什么？
要么 y 是黑点，要么 y 那一边的联通块里有至少两个黑点
对于满足第二个条件的情况，我们发现此时通过边 x→y 是“自由的”，即可以通过适当安排勾引顺序，使得通过后并不会被附加什么限制
我们该怎么刻画这种“自由通过”呢？

建一条 x→y 的有向边
然后把新图取反跑一遍bfs即可
草

F

完全想不到，挺好的qwq
计算期望，可以转化成：计算所有可能的版本的贡献之和 ans
首先考虑操作 x = x - x % i，i 属于 1 到 K，设 L = LCM(1,2,...,K)；若 L|x，则 x 不会变化；更进一步，若 x%L=c，则 x 最多减至 x-c，也就是说不管 x 经历哪些操作，最后的值都不会小于 x-x%L
设 a-a%L = b，则 b 是始终会贡献到答案里的，即 ans+=\(Kb\times n^{K-1}\)，我们只需要考虑 a%L 的部分，即令 a%=L，此时每个数的大小已经被限制到了 LCM(1,2,...,K=17)
我们这么刻画所谓“所有可能版本的贡献之和”（开始以自己的方式理解题解）：
最开始只有一个数组，也即是初始版本，接下来第 1 次迭代，选择数组里的每一个位置操作，都会形成一个新的版本，所以形成了 n 个版本；这是一个标准的树结构，所以接下来继续下去，第 k 次迭代时这一层会有 \(n^k\) 个版本；然后我们怎么计算所有版本的贡献呢？设当前为第 i 次迭代，根据题目，当我们选择数组的某一个位置时，产生的答案 a 就对应了树上往那个版本发展出去的“边”，这条边会被计算多少次呢？不是一次，而是所有包含该条边的方案的个数，所谓方案就是从根到叶子的一条链，所以就是从这条边往下的叶子节点个数，也就是 \(N^{K-i-1}\)
回到怎么计算，考虑 dp，f[i][j] 表示当前为第 i 次迭代，数字 j 在这次迭代所产生的所有版本中出现的次数，显然 f[0][j] 就是初始数组的 cnt[j]，转移方程这么考虑：
我们可以利用之前的树结构来考虑，对于一层里的一个版本（即一个数组），选择某个位置，该位置会更新给下一层 a-a%(i+1)，而其他数字原封不动地复制了一遍；也就是说每个数字 a 因为被选中的那一次而更新给了下一层的 a-a%(i+1)，因为没被选中而被 (N-1) 次地更新给了下一层的 a 本身。故：

\[f[i+1][j-j\% (i+1)] += f[i][j]\\ f[i+1][j] += f[i][j]*(N-1) \]

而我们也能得到答案的计算方式：对于 0<=i< K，f[i][j] 有：ans+=\(j*f[i][j]*N^{K-i-1}\)
这样的复杂度是 \(O(N+K*LCM(1,\dots,K))\)
但是注意到，我们计算dp部分的贡献时并不会用到 K 的值，所以我们可以用 LCM(1,...,K-1) 代替之，刚好能使复杂度除以 17

#include <cstdio>
using namespace std;
typedef long long ll;
const ll mod = 998244353;
const int INF = 720777; // 2^4 * 3^2 * 5 * 7 * 11 * 13
const int MAXN = 10000007;
int N, K; ll A, X, Y, M, f[18][INF]; // [0, K)
ll pn[20]; // power of n
void add(ll &x, ll y) { x = (x + y) % mod; }
int main()
{
	scanf("%d%lld%lld%lld%d%lld", &N, &A, &X, &Y, &K, &M);
	pn[0] = 1; for (int i=1; i<=17; i++) pn[i] = pn[i-1] * N % mod;
	ll L = 720720, ans = 0;
	for (int i=0; i< N; i++) {
		ll c = A % L, b = A - c;
		add(ans, K * b % mod * pn[K-1] % mod);
		f[0][c]++;
		A = (A * X + Y) % M;
	}
	for (int i=0; i< K; i++) {
		for (int j=0; j< L; j++) {
			add(ans, j * f[i][j] % mod * pn[K-i-1]);
			add(f[i+1][j], f[i][j]*(N-1)%mod);
			add(f[i+1][j-j%(i+1)], f[i][j]);
		}
	}
	printf("%lld\n", ans);
}