【笔记】网络流S

%%%GNAQ
让我们先高喊三声：“ GNAQ 太巨啦！！！”
所以这篇算是参考资料？（

无源汇上下界可行流

首先，我们要明确什么是无源汇上下界可行流。
一个闭环环流，每条边流量满足在 \([L_i, R_i]\) 范围内，每个点出流 \(=\) 入流，求可行解（给每个边分配流量）。
在原图上添加超级源点 \(\mathbb{S}\) 和超级汇点 \(\mathbb{T}\)。
枚举每条边，记为 \(e = (u, v | L, R)\)。在新的网络流图上添加 \(e' = (u, v, R-L)\)。然后添加 \((\mathbb{S}, v, L)\) 和 \((u, \mathbb{T}, L)\)。

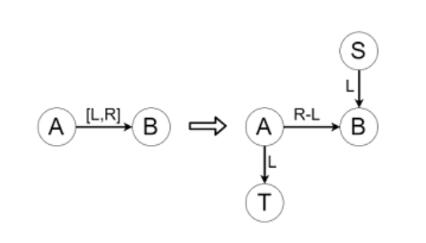
为什么要这么建流？
修改容量到 \(R_i-L_i\) 相当于先强制让每个边流 \(L_i\)，这是合法解所必须的。
在每条边流 \(L_i\) 的流量后，现在的图实际上不平衡，每个点的入流不一定等于出流。所以我们的目的，是在这个图上调整流量至平衡。

• \(u\) 被我们凭空制造了 \(L_i\) 流量，它需要从图上的某处流入 \(L_i\)，因此向超级汇点连边，容量 \(L_i\)，

为什么这么别扭？我们是在新图上跑最大流算法。算法会“认为”这个图是个空流量图。我们是要求算法给 \(u\) 塞入 \(L_i\) 流量，这样我们刚刚凭空添加的流量就有来由了。
但是这些流量实际上不需要流走，因为这些流量会在原图流走，填充边的下界。所以我们实际上是在新图中消灭这些多出来的流量。扔给我们自己建的点 \(\mathbb{T}\) 即可。
则如果这条边满流，就代表有办法从某处流入 \(u\) 点 \(L_i\) 的入流。

• \(v\) 被我们凭空减走了 \(L_i\) 流量，它需要把 \(L_i\) 流到图上的某处，因此从超级源点连边，容量 \(L_i\)，则如果这条边满流，就代表 \(v\) 点有办法向某处流走 \(L_i\) 的出流。

然后直接开跑最大流。最后需要检查 \(\mathbb{S}\) 的出边和 \(\mathbb{T}\) 的入边是不是都满流了，满了才有解。
要输出解怎么办？
根据残量网络可以获得一组合法解。其中每条边的流量就是 \(L_i\) 加上残量网络中这条边对应边的流量。

有源汇上下界可行流

先明确什么是有源汇上下界可行流。
相比上个问题，源点 \(\mathbb{S}\) 无需入流，出流量不受限制、汇点 \(\mathbb{T}\) 无需出流、入流量不受限制。其他点必须流量平衡。
我们能不能强行修改为上一个问题模型？可以。
我们让 \(\mathbb{T}\) 向 \(\mathbb{S}\) 连边，容量 \(+\infty\)，构建环流体系，使其平衡。
然后按之前的模型，新建超级源汇 \(\mathbb{SS}\) / \(\mathbb{TT}\)。
此后只需要求解上个问题。问题可能无解，注意判断。（判断方法一样）

有源汇上下界最大流

现在不单独问可行与否了，变成询问是否可行、若可行询问最大流。
我们不管别的，先按有源汇上下界可行流做一遍。
做完之后，思考一下这个残局上，各个边到底代表什么意义。
\(\mathbb{T}\) 到 \(\mathbb{S}\) 的边的反边容量即是这个可行流环流的总大小。
如果我们不看超级源点、超级汇点以及与之相关的边，只看 \(\mathbb{S} \rightarrow \mathbb{T}\) 的残量网络的话，此时图中还有部分边未满载，允许在残量网络上的部分边自由流。
此时直接从 \(\mathbb{S} \rightarrow \mathbb{T}\) （注意不是 \(\mathbb{SS}\) / \(\mathbb{TT}\)）跑最大流，则这个最大流即为答案。
理由：此最大流包括了
（1）\(\mathbb{T} \rightarrow \mathbb{S}\) 的反边容量会跑满，也即可行流环流的大小。
（2）除此之外还有 \(\mathbb{S} \rightarrow \mathbb{T}\) 的部分自由流，在可行流的基础上成为最大流。

有源汇上下界最小流

现在把最大流变成最小流，求解？
显然可以二分答案，然后跑上下界可行流，但不优美。
二分的方法是去调整那条 \(\mathbb{T} \rightarrow \mathbb{S}\) 的边的容量，然后做可行流。
那优美的做法是什么呢？
考虑最小流的本质在做什么：
最小化 \(\mathbb{T} \rightarrow \mathbb{S}\) 的边流量，那么考虑我们求解可行流的时候，本质是在跑一个 \(\mathbb{SS} \rightarrow \mathbb{TT}\) 的最大流
则这个最大流包括两部分流量，一部分经过 \(\mathbb{T} \rightarrow \mathbb{S}\) 的边，一部分不经过。我们只需要最大化不经过的部分，剩余经过的就是最小的可能流法了。
所以拆去 \(\mathbb{T} \rightarrow \mathbb{S}\) 的边，保留残量图，跑一次 \(\mathbb{T} \rightarrow \mathbb{S}\) 的最大流。也可以类比为一个强行退流操作，但保留了最低可行的方案。
为什么可行性有保障？因为这样跑最大流不会改变 \(\mathbb{S}\) 的出边和 \(\mathbb{T}\) 的入边是否满流。

• 也就是不会改变可行流的可行性。

如果有解，第一次跑算法，这些边一定会满流。第二次这些边一定不会被跑到（考虑图的样子 & 最大流通过找增广路运行）。
答案就是初次可行流的流量（也即 \(\mathbb{T} \rightarrow \mathbb{S}\) 的边流量）减去第二次最大流的流量。

• 若问题不保证有解，则还需一次有源汇上下界可行流验证。

上下界费用流

先不考虑存在负环的情况。
其实本身非常简单。
我们按题目要求建图，然后再应用之前对应的非费用流模型即可。
引入新的平衡流量的边的时候，我们为这种边设置 \(0\) 费用。
“类比网络流的建图即可” （——Leoly）

费用流消除负环

这个问题比较复杂，我们慢慢讲
在讲之前，我们先补充一个被遗漏的东西：可行流的另一种建边方式。
问题还是熟悉的无源汇上下界可行流问题。
我们先按照套路把下界去掉。然后，这次我们不连边，我们统计每个点 \(u\)：
如果有一条边 \((a, u)\) 指向这个点 \(u\)，让 \(e_u\) 加上这条边的下界。
如果有一条边 \((u, b)\) 从 \(u\) 流出，让 \(e_u\) 减去这条边的下界。
这样我们统计了每个点在原图上的盈余流量 \(e_u\)。
对于 \(e_u > 0\) 的点，它代表这个点要想办法流走这些流量。这些流量是我们强制把下界流满之后，积存在这个点的。
在新图上，和我们之前的思路一样，算法会认为这个点是没有流量的，我们需要给他直接流入 \(e_u\)，然后让算法运行，流走这些流量。
所以建边 \((\mathbb{S}, u, e_u)\) 即可。
同理，如果 \(e_u < 0\)，那么建边 \((u, \mathbb{T}, |e_u|)\) 即可。

• 为什么要讲这个东西？

考虑我们现在已经处理好了一个无源汇最小费用可行流，现在它出现了负环。
问题在于我们的费用流增广处理不了负环。
最小流实际在求一个费用最优化问题。记得上下界问题的处理，使用了一个非常好的思想：先满足别的条件，再逐步调整至流量平衡。
那如果我先让所有的只要费用为负的边都满流，然后在非负图上跑最小费用最大流，不断地调整流量，并不会改变我们在对费用做最优化的问题本质。
为什么？因为我们一开始达到了流量不平衡情况下的最优解，此后我们在选择最小费用的增广路调整流量。
我们一直维持了最优化的条件，逐步解决了平衡条件。
所以我们如果沿用上面的思路解决无源汇最小费用可行流的话，在计算完 \(e_u\) 之后，先不着急连边。
我们把所有负边满流，然后继续更新 \(e_u\)。之后我们再建图，在新图上跑最小费用最大流。
注意方案的计算，思路和之前的过程一样。
在处理上下界、消除负环的过程中，我们建的所有为了平衡流量的边（即不在原图上的边）费用都为 \(0\)。

费用流消除负环EX

进阶版
考虑我们现在已经处理好了一个有源汇最小费用可行/最大流，现在它出现了负环。
（这玩意因为会有一个 \(\mathbb{T} \rightarrow \mathbb{S}\) 的 \(0\) 费边，所以几乎一定会出负环）
你大可以对这个图再做一次上面的过程（建立源点汇点，强制把边满流……）
但是考虑我们在处理不带费用的问题的时候，已经建立了一对超级源汇了。
而且这对超级源汇与负环没有任何关系，它是平衡流量用的。
现在我们还是在平衡流量，所以复用这对源汇即可。

• 注意：如果是最大流，还是照例跑两次。

\(\mathbb{T} \rightarrow \mathbb{S}\) 连边 \((+\infty, -x)\)，其中 \(x\) 是一个大数。
之后按套路将所有的负边强制满流，建超级源汇。
直接在超级源汇上跑一次最小费用最大流，由于 \(-x\) 可以保证最优，此时原图 \(\mathbb{S} \rightarrow \mathbb{T}\) 已经达到了最大流。
计算费用中 \(−x\) 的个数，即可得到最大流的数值。抹去这些 \(-x\)，就可以得到费用答案。

经典模型：路径覆盖类问题。

Dilworth 定理

基础定义：

• 偏序集，这个大家都懂：自反性，反对称性，传递性
• 偏序集可以用 DAG 来表示，我个人比较喜欢这种形象化的东西。
• 可比：在偏序里可以比较，在 DAG 里体现为，两个元素 \(u, v\) 可比，则可以从 \(u\) 沿有向边走向 \(v\)，或从 \(v\) 到 \(u\)。
• 链：DAG 上的链，体现为任意两元素可比。
• 不可比：在 DAG 里体现为 \(u, v\) 互相走不到对方。
• 反链：一个序列 \(u_1, u_2, \cdots, u_k\)，任意两元素不可比。

定理：把一个 DAG（一个有限偏序集）完全划分成若干个不相交链的最小链个数 \(=\) 这个 DAG 上的最长反链的长度。
直接应用一般是求一些最长升降序列的问题。
间接应用很多，一般是拿这个转化问题（注意是等号，可以两个方向用）。
比如……

最小路径 / 链覆盖问题

• 最小路径覆盖：给一个 DAG，用尽量少的、点不相交的简单路径覆盖整个图的所有点。

这也就是 Dilworth 定理求的那个划分。
做法
将图中的每个点拆成两个点 \(u, u'\)。
如果原图中有 \((u, v)\)，连接 \(u \rightarrow v'\)。
这玩意是个二分图。跑个最大匹配，答案就是原图点数 \(n -\) 最大匹配数 \(z\)。
为什么？我们初始每个点各自作为一个路径。每次匹配两个点，代表把两个点的路径合并到一起。
每次匹配必然对应两条路径首尾点的合并。画图即得。
先提一嘴传递闭包。对一个图求传递闭包，本质就是求一个 \(01\) 矩阵 \(\mathbf{C}_{nm}\)。
其中 \(\mathbf{C}_{ij}\) 表示 \(i\) 点可不可以通过沿着图上的有向边走到 \(j\)。（无向边拆为两条）
这玩意很简单，用 Floyd 即可求。
最小链覆盖：最小路径覆盖的改版，这次要求不同链的点可以相交。
做法：先做传递闭包，然后根据 \(\mathbf{C}_{ij}\) 对二分图连边，答案还是那么求。
为什么对？严格证明我不会，感性理解：
用传递闭包可以跳过被已选链“占用”的点合并链（画图）。此外我们可以贪心地应合尽合，能够合并的链，都合了准没错。
不能合并的链，就算求了传递闭包，在二分图里显然也连不上边。

经典模型：最大权闭合子图

最小割问题

给你一个网络流图 \(\mathbf{G}\)，求它的最小割，就是：
选择一些边（一个边集子集） \(\mathbf{E_{\mathrm{sub}}}\)，把这些边去掉之后，原图不能从 \(\mathbb{S}\) 走到 \(\mathbb{T}\)。
求出这些边的流量和最小的边集。
这个问题怎么做？
求这个网络流图的最大流，最大流的数值即是最小割的数值。
最大流 \(=\) 最小割。
为什么？主要思路是灵活的反证法，利用残量网络的性质。

最大权闭合子图

这个问题是这样的：

• 给你一个关系：选了某 \(x\) 就必须选 \(y\)。选某些点有收益，选某些点有代价（负收益）。问你怎么选收益最大。

严谨的定义大概是：

• 一个子图（图点集的子集），如果它的所有的出边所指向的点都在这个子图当中，那么它就是闭合子图。一个图中点权和最大的闭合子图就是最大全闭合子图。

现在我们了解了它的定义，但这个问题怎么做呢？
我们把原图保留，此外新添源汇 \(\mathbb{S, T}\)。
如果 \(u\) 点权 \(w_u\) 非负，连边 \((\mathbb{S}, u, w_u)\)。
如果 \(v\) 点权 \(w_v\) 为负，连边 \((v, \mathbb{T}, |w_v|)\)。
原图上本来的边添加流量 \(+\infty\)。
然后我们求个最小割 \(z\)，所有正权值点的权值和减去 \(z\) 就是答案。

经典模型：二分图若干定理

König 定理

二分图的最小点覆盖：选取最少的点数，使这些点和所有的边都有关联（把所有的边的覆盖）。
二分图最大匹配：二分图左右两个点集中，选择有边相连的两个匹配成一对（每个点只能匹配一次），所能达到的最大匹配数。
König 定理指出：
二分图最小点覆盖 \(=\) 二分图最大匹配。
它的一些推论：
最小点覆盖 \(=\) 最大匹配。
最大独立集 \(=\) 总点数 \(-\) 最小点覆盖。
二分图最大独立集：选若干个点组成一个集合，使得这些集合的点互不相连（无向边）。
它的证明需要引用到最小割最大流定理的证明，所以也不讲了。

杂乱

一个不知道有没有用的小性质。
在一个二分图中，如果删去一条边能够使这个图的最大匹配减小 \(1\) 的话，那么这条边一定在残量网络中满流，并且它所连接的两个点一定不在同一个边双连通分量当中。
首先满流的条件一定要有，不满流则这条边不在最大匹配内。
如果在同一个边双里，删去后可以在这个连通分量的内部进行增广，也就是说可以找到另一组不需要使用当前边的最大匹配。

霍尔定理及其推论

设一个二分图 \(\mathbf{G} = \{ \mathbf{V_1}, \mathbf{V_2}, \mathbf{E} \}\)。
设 \(\mathbf{A} \subseteq \mathbf{V_1}\)，记 \(\mathbf{V_2}\) 集合中与 \(\mathbf{A}\) 相连的点为 \(N(\mathbf{A})\)。
如果这个图有完美匹配（即大小等于 \(\min(|\mathbf{V_1}|, |\mathbf{V_2}|)\) 的匹配），则：

\[\forall \mathbf{A} \subseteq \mathbf{V_1}, |\mathbf{A}| \leqslant |N(\mathbf{A})| \]

推论：
假设 \(|\mathbf{V_1}| \leqslant |\mathbf{V_2}|\)，最大匹配的大小为：

\[|\mathbf{V_1}| - \underset{\mathbf{A} \subseteq \mathbf{V_1}}\max(|\mathbf{A}| - |N(\mathbf{A})|) \]

霍尔定理及其推论：应用题
二分图 \(\mathbf{G}\) 中两个点集各包含 \(n\) 个点。\(n \leqslant 100\)。
找出 \(k\) 个完备匹配，使其互不相交。（提升：匹配是一个边集）
定义：\(K\) − 正则二分图：每个点的度数均为 \(K\)。
根据 Hall 定理，我们容易推出：若一个二分图是 \(K\) − 正则二分图，则其存在 \(K\) 个不相交的完备匹配。
网络流做个度数限制，验证一下能不能提取出原图的 \(K\) − 正则二分子图，从而判断解的存在性。

• 如何输出方案？

提出满流边就是子图，对提出的子图求 \(K\) 次完备匹配即可，正确性根据 Hall 定理容易证明。

平面图 - 对偶图

平面图是什么相信大家都已经了解了。
平面图的对偶图：把每个面视作一个点，邻面连边。
平面图和对偶图的某些问题可以互相转化。
平面图最小割 \(\Longleftrightarrow\) 对偶图最短路。
一般题目会给你一个非常友好的平面图，一般是棋盘图（因为平面图判定算法不会有人考）。
或者转化之后是这样的图。在上面跑最小割就是在对偶图上跑最短路。
证明？其实较为简单。考虑把每个最小割设出来，然后可以规定一个对应关系，使得它和对偶图的所有 \(\mathbb{S} \rightarrow \mathbb{T}\) 路建立双射。