【笔记】动态规划

一些模型？

期望 dp

f[s] 表示当前状态 s ，到达终态 T 所需的期望步数，那么有 $$f[s] = \sum_{s'} p[s\rightarrow s']\times(f[s']+1)$$
s' 就是下一步可以到达的所有情况，有时是个方程

条件期望：E(期望得分) = P(可得分概率) * E(可得分条件下的期望得分) ，两部分分开算

状压 dp

获取 x 的二进制的最低位的 1 ： x & (-x)
去除 x 的二进制的最低位的 1 ： x &= (x-1)
判断 x 的状压集合是 y 的子集： ((a | b) ^ b) == 0
枚举 S 子集： for (int S1=S; S1; S1=(S1-1)&S) （计算知复杂度 O(3^n)）
获取 a 的第 b 位： (a >> b) & 1
将 a 的第 b 位设置为 0 ： a &= ~(1 << b)
将 a 的第 b 位设置为 1 ： a |= (1 << b)
将 a 的第 b 位取反 ： a ^= (1 << b)
补集： ~a
差集： a & (~b)
对称差： a ^ b
判断 x 是否为 2 的幂： x & (x-1) == 0
高维前缀和

树上背包的复杂度

UPD：复杂度正确前提是所有边界都足够紧凑，下面的代码是错的，改天再改
f[u][i] 表示 u 的子树花费 i 的最大价值，则有

\[f[u][i] = max(f[u][i], f[u][i-j]+f[v][j]+w(...)) \]

for (int o=fst[x]; o; o=e[o].pre) if (e[o].v!=fa) {
	dfs(e[o].v, x);
	for (int i=K; i>=0; i--) {
		for (int j=0; j<=i; j++) {
			f[x][i] = max(f[x][i], f[x][i-j]+f[e[o].v][j]+w(...));
		}
	}
}

这个 w 就是选择 f[v][j] 产生的全部价值，不能有后效性，不然怎么叫 dp
看起来是 O(NK^2) ，实际上是 O(NK) 的
另外关于枚举顺序的问题，对于上面的 i ，显然要倒叙枚举；对于 j 则必须正序枚举，因为若最后枚举 j=0 ，会把 j!=0 得到的信息再用 j=0 更新一次

单调队列优化 dp

什么单调？
如果你当前的答案是从队首转移的，那肯定是队列对答案单调，在满足这个的前提下再考虑其他的单调
如果答案是通过队列的长度之类的来更新，再根据情况看看怎么保证队列合法的同时快速掐头去尾

[POI2014]PTA-Little Bird
设 f[i] 表示到达 i 的最小代价，那么首先有 \(f[i] = min_{i-k\leq j\leq i-1}\lbrace f[j] + [d[j]\leq d[i]]\rbrace\)
我们令维护队列首先满足 f 单调不降，其次满足 d 单调不升，每次通过队头转移即可。由于这题所有的代价是相同的都是 1，所以这么做是正确的

[POI2011]TEM-Temperature
考虑队列即为以当前 i 为最后一天的最长段，当前这一段如果合法，需要满足每一天的温度是前一天的温度和这一天的下限取max，也就是前面所有天的下限取max，且不超过这一天的上限
那么我们需要考虑的就是前面所有天的下限的最大值，如果超过当前天的上限，则 l++ 使得max减小，所以我们维护的单调队列是按下限单调下降的
画一个图是这样的：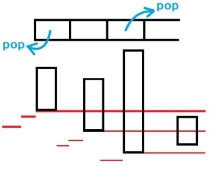

[CSP-S2019] 划分
这一类问题的要求是：将数组划分为若干段，满足这些段的和单调不减
贪心地认为，分的段数越多，每段越小，答案越小
可能有一个结论：所有段的平方和最小 等价于 段数最多 等价于 最后一段尽量小
所以设 f[i] 表示考虑前 i 个的合法解，最后一段可以取到的最小值
\(f[i] = min\lbrace s[i]-s[j]\rbrace, (f[j]\leq s[i]-s[j])\)
括号内条件即 \(f[j]+s[j]\leq s[i]\)，考虑到转移的 j 越大越好，且 s[i] 递增，所以维护一个下标递增且 f[]+s[] 递增的队列就行了

斜率优化

表示成线性规划的形式，就斜率单调维护一个单调队列
或者你想成一个一次函数，维护一个凸包时，每次加一条线都要保证交点横坐标单调

[USACO08MAR]Land Acquisition G 按 w 递增排序得到 h 递减的序列，\(f[i] = min\lbrace f[j] + h[j+1]*w[i]\rbrace\)，内部是一个关于 w[i] 的一次函数，而且 f 递增，h 递减，w 递增，非常标准

// y = kx+b, k = , b = ;
double cal(int i, int j) // calculate the intersection point's x
{
	double dk = k(i) - k(j), db = b(j) - b(i);
	return db / dk;
}

Q[1] = 0; // f[0] = 0;
int l = 1, r = 1; // [l, r]
for (int i=1; i<=N; i++) { // f[i] = k * x(i) + b + C(i);
	while (l< r && cal(Q[l], Q[l+1])< x(i)) l++;
	f[i] = k(Q[l]) * x(i) + b(Q[l]) + C(i);
	while (l< r && cal(Q[r-1], i)>=cal(Q[r], i)) r--;
	Q[++r] = i;
}