【笔记】二分图

写一种能方便我记忆的口胡

对于一个二分图，我们定义：
最大边独立集（感觉 最大匹配 这名字反倒容易混）：最大的边集，满足对于其中任意两条边，都没有共同顶点
最小点覆盖：最小的点集，满足对于图中任意一条边，都存在一个顶点属于这个点集
最大点独立集：最大的点集，满足对于其中任意两个顶点，都没有连边
最小边覆盖：最小的边集，满足对于图中任意一个顶点，都存在一条以其为端点的边属于这个边集

先给出结论：（最大边独立集 = 最小点覆盖） + （最大点独立集 = 最小边覆盖） = N（总点数）
然后口胡
如图，我们直接假设最优解的形式，当取到最大边独立集时，我们记最大边独立集所含点集为 V1 ，其余点集为 V2
对于点集 V1 中不属于最大边独立集的边我们无视掉就好了（虚线）

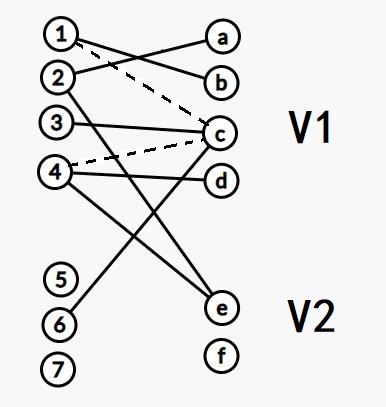
显然可以贪心地证明这个图具有性质：

1. V2 中任意两点间无边
2. 对于取到的边独立集中任意一条边，其至多只有一个顶点与 V2 中的顶点有边

然后我们直接钦定上述四个定义对应的是什么（这是不是都能出一个构造题了）

A. 最大边独立集： V1 所含实线边
B. 最小点覆盖：V1 所含实线边中，与 V2 有边相连的一端顶点（没有则任意一端）
C. 最大点独立集：V1 所含实线边中，与 V2 无边相连的一端顶点（没有则任意一端），并上 V2
D. 最小边覆盖：V1 所含实线边，并上与 V2 相连的所有边

显然 A = B，C = D，且 B + C = N（总点数），于是假装证毕

若干性质：
有向图的最小路径覆盖（路径两两不含公共点）：等于 N - 对应二分图的最大边独立集（最大匹配）
口胡：考虑初始一个顶点算一条路径，就有 N 条，选择一条边连接两个路径，就会使总路径数减 1 ；然后考虑路径两两不相交的条件，等价于对于任意一个顶点，其出度和入度都不会超过 1 ，出度就是二分图左划分上引出的边，入度就是右划分上被连的边，于是对应边独立集的定义

旬牙利（以及类似思路的“暴力”做法？）
upd: 反正现在被 dinic 替代了（
KM（强行抄板子）
建图，网格图（横纵坐标作为两个点集），奇数偶数环（黑白染色），二分图上两点路径长奇偶性至于是否在同一划分有关——用来推性质
对于点集的二划分模型，将不能同时属于同个点集的两点连边，然后跑一遍黑白染色判断是否合法

同个划分内的点彼此无关，不同划分间的点存在关联貌似没什么用