【笔记】Aho-Corasick 自动机

一到校就没怎么打代码了qwq

对文本串的多模板匹配。
和 KMP 非常类似，所以先回顾一下 KMP 。
对于文本串的当前匹配位置，我们得到其与模板串的最大匹配长度
对于 \(next\) 数组我们的定义也是该前缀中最大的公共前/后缀
这个“最大”保证了我们能够自然地得到“次大”及之后，这种次序关系保证了我们不会遗漏任何一种情况，也不会使状态机出现环

现在考虑多模板匹配，自然而然地我们先建一棵 Trie 树，默认边代表字符
假设对于文本串的当前匹配位置，我们能得到其在所有模板串中的最大匹配长度，即在 Trie 上的最深节点（若有多个，则按一定规则排序，比如字典序，这也是保证失配边“有序”的基础之一）
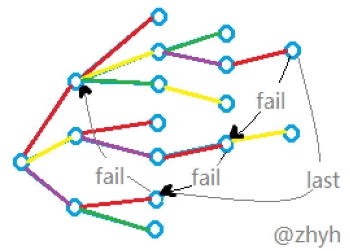
我们要做的事有两件：考察当前是否是某些模板串的末尾（ \(last\) 数组）；匹配文本串的下一个字符时我们应该跳到树上的哪一个节点（ \(fail\) 数组）。

先考虑熟悉的 \(fail\) 吧
显然 \(fail[0] = 0\) ，另外 \(0\) 节点的子节点的 \(fail\) 也等于 \(0\) （第一个节点就匹配失败了就没得匹配了）
对于树上的链 \(0\to \dots \to u\to v\) ，且 \(u\to v\) 边字符为 \('c'\) ，则其 \(fail\) “最多”等于 \(fail[u]\) 的位置接上 \('c'\) ，前提是 \(nxt[fail[u]][c]=1\)
再不济，就继续匹配下去：

while (v && !nxt[v][c]) v = fail[v];

最后还是传统艺能：

fail[u] = nxt[v][c];

这就是 \(fail\) 数组了。
关于 \(last\) 数组，我们来定义一下：\(last[j]\) 指树上当前位置（链），满足某个模板串 恰好是当前链的后缀 的 最长的那一个。（同样的，我们定义个字典序之类的来排序那些同样长度的模板串）
首先， \(last[0] = 0\) ，而 \(0\) 节点的子节点的 \(last\) 也等于 \(0\)
那么怎么求呢？我们发现， \(last\) 数组无非就是 \(fail\) 数组依次下去的那些链中，属于结束节点（ \(flg = 1\) ）的那几个。前者是后者的子集。
那么就有式子：

last[u] = flg[fail[u]] ? fail[u] : last[fail[u]];

这就是了。

然后回到我们一开始要做的两件事：
考察当前是否是某些模板串的末尾：顺着 \(last\) 跳即可。对应下文 print 函数
匹配文本串的下一个字符时我们应该跳到树上的哪一个节点：失配就顺着 \(fail\) 跳即可
提一下，定义保证沿着 \(fail\) 跳，深度是单调不增的；至于 \(last\) ，是个 \(fail\) 的产物

最后还有一个大优化：

int u = nxt[x][c];
//if (!u) continue;
if (!u) { nxt[x][c] = nxt[fail[x]][c]; continue; }
Q.push(u);

那么我们跳失配时就可以不用写

while (v && !nxt[v][c]) v = fail[v];

因为假设存在不得不写这句话的情况，和上面的代码功能就矛盾了
虽然我还是把这句话保留了（

#include <queue>
#include <cstdio>
#include <cstring>
using namespace std;
const int MAXN = 1000005;
struct AC {
	int nxt[MAXN][26], flg[MAXN], cnt;
	int fail[MAXN], last[MAXN];
	// ...--'c'-->x = ...--'c'-->fail[x]
	AC() {
		cnt = 0;
		memset(nxt, 0, sizeof(nxt));
		memset(flg, 0, sizeof(flg));
		memset(fail, 0, sizeof(fail));
		memset(last, 0, sizeof(last));
	}
	void insert(char S[], int id) {
		int len = strlen(S), p = 0;
		for (int i=0; i< len; i++) {
			int c = S[i] - 'a';
			if (!nxt[p][c]) nxt[p][c] = ++cnt;
			p = nxt[p][c];
		}
		flg[p] = id;
	}
	void getFail() {
		queue<int> Q;
		fail[0] = 0;
		for (int c=0; c< 26; c++) {
			int u = nxt[0][c];
			if (u) fail[u] = 0, Q.push(u), last[u] = 0;
		}
		while (!Q.empty()) {
			int x = Q.front(); Q.pop();
			for (int c=0; c< 26; c++) {
				int u = nxt[x][c];
				//if (!u) continue;
				if (!u) { nxt[x][c] = nxt[fail[x]][c]; continue; }
				Q.push(u);
				int v = fail[x];
				while (v && !nxt[v][c]) v = fail[v];
				fail[u] = nxt[v][c];
				last[u] = flg[fail[u]] ? fail[u] : last[fail[u]];
			}
		}
	}
	void find(char S[]) {
		int len = strlen(S), j = 0;
		for (int i=0; i< len; i++) {
			int c = S[i] - 'a';
			while (j && !nxt[j][c]) j = fail[j];
			j = nxt[j][c];
			if (flg[j]) print(j);
			else if (last[j]) print(last[j]);
		}
	}
	void print(int j) {
		if (j) printf("%d\n", flg[j]), print(last[j]);
	}
} ac;
int N; char S[MAXN];
int main()
{
	scanf("%d", &N);
	for (int i=1; i<=N; i++) scanf("%s", S), ac.insert(S, i);
	ac.getFail(), scanf("%s", S), ac.find(S);
}