第三次作业
| 这个作业属于哪个课程 | https://edu.cnblogs.com/campus/qdu/DS2020 |
|---|---|
| 这个作业要求在哪里 | |
| 这个作业的目标 | <掌握线性表中元素的前驱、后续的概念;熟悉相关算法;对线性表相应算法的时间复杂度进行分析;理解顺序表、链表数据结构的特点> |
| 学号 | |
| 一、实验目的 | |
| 1、掌握线性表中元素的前驱、后续的概念。 | |
| 2、掌握顺序表与链表的建立、插入元素、删除表中某元素的算法。 | |
| 3、对线性表相应算法的时间复杂度进行分析。 | |
| 4、理解顺序表、链表数据结构的特点(优缺点)。 |
二、实验预习
说明以下概念:
1、线性表:线性表是n个具有相同特性的数据元素的有限序列。数据元素是一个抽象的符号,其具体含义在不同的情况下一般不同。在稍复杂的线性表中,一个数据元素可由多个数据项组成,此种情况下常把数据元素称为记录,含有大量记录的线性表又称文件。线性表中的个数n定义为线性表的长度,n=0时称为空表。
2、顺序表:顺序表是在计算机内存中以数组的形式保存的线性表,线性表的顺序存储是指用一组地址连续的存储单元依次存储线性表中的各个元素、使得线性表中在逻辑结构上相邻的数据元素存储在相邻的物理存储单元中,即通过数据元素物理存储的相邻关系来反映数据元素之间逻辑上的相邻关系,采用顺序存储结构的线性表通常称为顺序表。
3、链表:链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。
三、实验内容和要求
1、阅读下面程序,在横线处填写函数的基本功能。并运行程序,写出结果。
#include<malloc.h>
#define ERROR 0
#define OK 1
#define INIT_SIZE 5 /*初始分配的顺序表长度*/
#define INCREM 5 /*溢出时,顺序表长度的增量*/
typedef int ElemType; /*定义表元素的类型*/
typedef struct Sqlist{
ElemType *slist; /*存储空间的基地址*/
int length; /*顺序表的当前长度*/
int listsize; /*当前分配的存储空间*/
}Sqlist;
int InitList_sq(Sqlist *L);/*顺序表初始化*/
int CreateList_sq(Sqlist *L,int n); /*创建一个长度为n的顺序表*/
int ListInsert_sq(Sqlist *L,int i,ElemType e);/*将新元素e插入到表中的第i个位置*/
int PrintList_sq(Sqlist *L); /*输出顺序表的元素*/
int ListDelete_sq(Sqlist *L,int i); /*删除第i个元素*/
int ListLocate(Sqlist *L,ElemType e); /*查找值为e的元素*/
int InitList_sq(Sqlist *L){
L->slist=(ElemType*)malloc(INIT_SIZE*sizeof(ElemType));
if(!L->slist) return ERROR;
L->length=0;
L->listsize=INIT_SIZE;
return OK;
}/*InitList*/
int CreateList_sq(Sqlist *L,int n){
ElemType e;
int i;
for(i=0;i<n;i++){
printf("input data %d",i+1);
scanf("%d",&e);
if(!ListInsert_sq(L,i+1,e))
return ERROR;
}
return OK;
}/*CreateList*/
/*输出顺序表中的元素*/
int PrintList_sq(Sqlist *L){
int i;
for(i=1;i<=L->length;i++)
printf("%5d",L->slist[i-1]);
return OK;
}/*PrintList*/
int ListInsert_sq(Sqlist *L,int i,ElemType e){
int k;
if(i<1||i>L->length+1)
return ERROR;
if(L->length>=L->listsize){
L->slist=(ElemType*)realloc(L->slist,
(INIT_SIZE+INCREM)*sizeof(ElemType));
if(!L->slist)
return ERROR;
L->listsize+=INCREM;
}
for(k=L->length-1;k>=i-1;k--){
L->slist[k+1]= L->slist[k];
}
L->slist[i-1]=e;
L->length++;
return OK;
}/*ListInsert*/
/*在顺序表中删除第i个元素*/
int ListDelete_sq(Sqlist *L,int i){
if(i<1||i>L->length) return 0;
for(int j;j<L->length;j++)
L->slist[j-1]=L->slist[j];
L->length--;
return 1;
}
/*在顺序表中查找指定值元素,返回其序号*/
int ListLocate(Sqlist *L,ElemType e){
int i=0;
while ((i<=L->length)&&(L->slist[i]!=e))
i++;
if(i<=L->length&&(L->slist[i]=e))
return i+1;
else
return ERROR;
}
int main(){
Sqlist sl;
int n,m,k;
printf("please input n:"); /*输入顺序表的元素个数*/
scanf("%d",&n);
if(n>0){
if(n>0){
printf("\n1-Create Sqlist:\n");
InitList_sq(&sl);
CreateList_sq(&sl,n);
printf("\n2-Print Sqlist:\n");
PrintList_sq(&sl);
printf("\nplease input insert location and data:(location,data)\n");
scanf("%d,%d",&m,&k);
ListInsert_sq(&sl,m,k);
printf("\n3-Print Sqlist:\n");
PrintList_sq(&sl);
printf("\nplease input delete location:location\n");
scanf("%d",&m);
ListDelete_sq(&sl,m);
printf("\n4-Print Sqlist:\n");
PrintList_sq(&sl);
printf("\nplease input data:data\n");
scanf("%d",&m);
n=ListLocate(&sl,m);
if(n>=0)
printf("This data is No:\t%d\n",n);
scanf("%d",&n);
printf("\n");
}
else
printf("ERROR");
return 0;
}
}
-
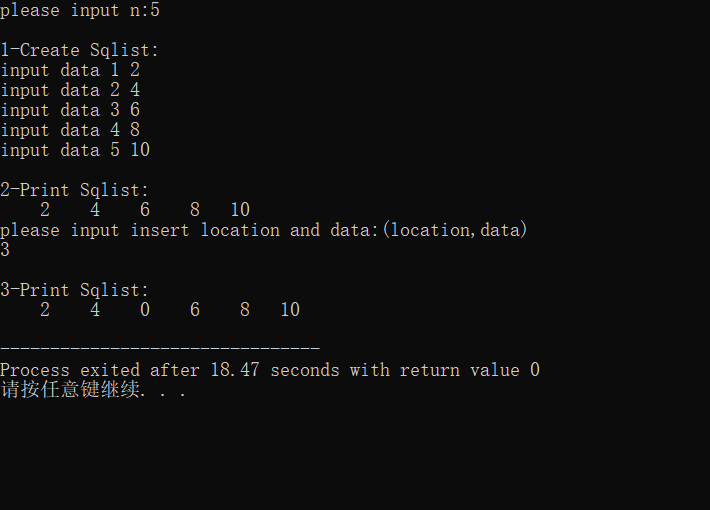
运行结果:
![]()
-
算法分析:
先要定义一个顺序表,接着再分别定义不同的运算函数,之后再编写每一个运算函数的函数体,紧接着在主函数中调用InitList_sq(&sl)函数初始化,然后调用InitList_sq()创建顺序表,调用PrintList_sq()函数输出该顺序表中元素的值;然后调用ListInsert_sq()函数,进行插入操作,并输出插入新元素后的状态。
顺序表存储需要预留空间,算法空间复杂度O(n)
算法时间复杂度O(1)
2、为第1题补充删除和查找功能函数,并在主函数中补充代码验证算法的正确性。
删除算法代码:
int ListDelete_sq(Sqlist *L,int i) {
int k = 0;
if(i<1||i>(L->length)) return ERROR;
for(k = i-1;k<L->length-1;k++){
L->slist[k] = L->slist[k+1];
}
L->slist[L->length-1]=NULL;
L->length--;
return OK;
}
-
运行结果:
![]()
-
算法分析:
输入线性表的元素个数,然后构建一个新的线性表;连续用ListDelete_sq函数删除元素,将其元素输出;在下一步中输入删除元素的位置,输出运行后的线性表。
算法时间复杂度:O(n)
查找算法代码:
int ListLocate(Sqlist *L,ElemType e) {
int k = 0;
for(k = 0;k<L->length;k++){
if(e==L->slist[k]) return k+1;
}
return ERROR;
}
-
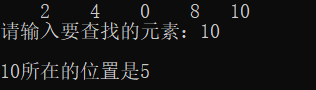
运行结果:
![]()
-
算法分析:
输入线性表的元素个数,输入线性表元素,然后构建一个新的线性表并输出;用ListLocate函数查找元素,将其元素的位置输出;在下一步中输入元素,输出此元素位置。
算法时间复杂度:O(n)
3、阅读下面程序,在横线处填写函数的基本功能。并运行程序,写出结果。
#include <stdio.h>
#include <stdlib.h>
#include<malloc.h>
#define ERROR 0
#define OK 1
typedef int ElemType; /*定义表元素的类型*/
typedef struct LNode { /*线性表的单链表存储*/
ElemType data;
struct LNode *next;
} LNode,*LinkList;
LinkList CreateList(int n); /*创建一个长度为n的链表*/
void PrintList(LinkList L); /*输出带头结点单链表的所有元素*/
int GetElem(LinkList L,int i,ElemType *e); /*在单链表中查找第i个结点的元素*/
LinkList CreateList(int n) {
LNode *p,*q,*head;
int i;
head=(LinkList)malloc(sizeof(LNode));
head->next = NULL;
p=head;
for(i=0; i<n; i++) {
q=(LinkList)malloc(sizeof(LNode));
printf("input data %i:",i+1);
scanf("%d",&q->data); /*输入元素值*/
q->next=NULL; /*结点指针域置空*/
p->next=q; /*新结点连在表末尾*/
p=q;
}
return head;
}/*CreateList*/
void PrintList(LinkList L) {
LNode *p;
p=L->next; /*p指向单链表的第1个元素*/
while(p!=NULL) {
printf("%5d",p->data);
p=p->next;
}
}/*PrintList*/
int GetElem(LinkList L,int i,ElemType *e) {
LNode *p;
int j=1;
p=L->next;
while(p&&j<i) {
p=p->next;
j++;
}
if(!p||j>i)
return ERROR;
*e=p->data;
return OK;
}/*GetElem*/
int main() {
int n,i;
ElemType e;
LinkList L=NULL; /*定义指向单链表的指针*/
printf("please input n:"); /*输入单链表的元素个数*/
scanf("%d",&n);
if(n>0) {
printf("\n1-Create LinkList:\n");
L=CreateList(n);
printf("\n2-Print LinkList:\n");
PrintList(L);
printf("\n3-GetElem from LinkList:\n");
printf("input i = ");
scanf("%d",&i);
if(GetElem(L,i,&e))
printf("No%i is %d\n",i,e);
else
printf("not exists");
} else
printf("ERROR");
return 0;
}
-
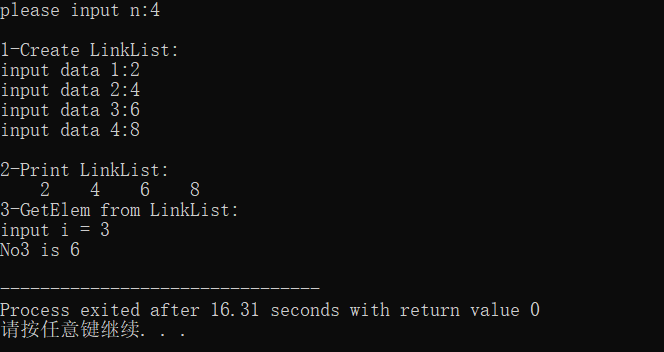
运行结果:
![]()
-
算法分析:
创建带头结点的单链表,首先输入结点数,然后依次输入各个结点的值;输出单链表中的值;输入查找元素的位置,输出对应元素的值。
算法时间复杂度:O(n)
4、为第3题补充插入功能函数和删除功能函数。并在主函数中补充代码验证算法的正确性。
插入算法代码:
int LengthList(LinkList L);/*求链表的长度*/
int InsertList(LinkList L,int i,ElemType* e);/*在第i个位置插入元素*/
int LengthList(LinkList L){
int i = 0;
LNode* p = NULL;
for(p = L;p->next!=NULL;p=p->next){
i++;
}
return i;
}
int InsertList(LinkList L,int i) {//插在第i个位置的后面,如果要插在表头,则i=0
if(i<0||i>LengthList(L)) return ERROR;
LNode* p;
LNode* q;
LNode* r;
int e = 0;
r = (LinkList)malloc(sizeof(LNode));
printf("输入要插入的元素:");
scanf("%d",&e);
r->data = e;
if(i==0){
p = L;
q = p->next;
p->next = r;
r->next = q;
return OK;
}
int j = 0;
for(p = L;j < i;j++){
p=p->next;
}
q = p->next;
p->next = r;
r->next = q;
return OK;
}
-
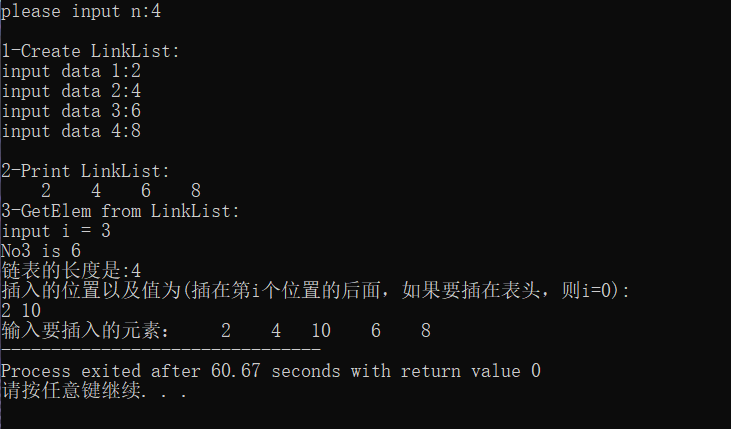
运行结果:
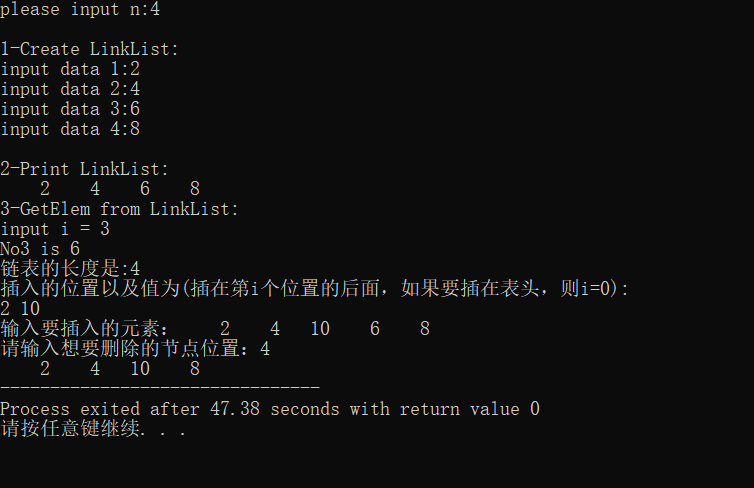
![]()
-
算法分析:
创建带头结点的单链表,首先输入结点数,然后依次输入各个结点的值;输出单链表中的值;输入插入元素的位置和插入的元素,输出单链表中的值。
算法时间复杂度:O(1)
删除算法代码:
int DeleteList(LinkList L,int i) {
if(i<1||i>LengthList(L)) return ERROR;
LNode* p;
LNode* q;
LNode* r;
int j = 0;
for(p = L;j < i-1;j++){
p=p->next;
}
q=p->next;
r=q->next;
p->next = r;
free(q);
return OK;
}
-
运行结果:
![]()
-
算法分析:
创建带头结点的单链表,首先输入结点数,然后依次输入各个结点的值;输出单链表中的值;输入删除元素的位置,输出单链表中的值。
算法时间复杂度:O(n)
5、循环链表的应用(约瑟夫回环问题)
n个数据元素构成一个环,从环中任意位置开始计数,计到m将该元素从表中取出,重复上述过程,直至表中只剩下一个元素。
提示:用一个无头结点的循环单链表来实现n个元素的存储。
- 算法代码:
#include <stdio.h>
#include <stdlib.h>
#include<malloc.h>
typedef struct lnode{/*结点类型定义*/
int data;
struct lnode *next;
} node, *nodeptr;
nodeptr creat() {/*创建循环单链表*/
nodeptr l,p, q;
int i ,n, e;
printf("please input n:" );
scanf("%d", &n);
l= (nodeptr)malloc(sizeof(node));
scanf(" %d",&e) ;
q=l;
q->data=e;
for(i=2;i<=n;i++) {
p= (nodeptr) malloc(sizeof (node));
scanf("%d" , &e) ;
p->data=e;
q->next=p;
q=p;
}
q->next=l;
return l;
}
int out (nodeptr l) {/*输出单链表的元素*/
nodeptr p;
p=l;
if(!p) return 0;
printf("%3d", p->data) ;
p=p->next;
while(p!=l) {
printf("%3d", p->data) ;
p=p->next;
}
printf("\n");
}
nodeptr joseph (nodeptr l){ /*约瑟夫回环函数*/
nodeptr p,q, r;
int val, k, m;
printf(" please input m:");
scanf("%d" , &m);
p=l;k=1;
while(p->next!=p)
if (k<m){
k++;
q=p;
p=p->next;
}
else{
val=p->data;
r=p;
p=p->next;
q->next=p;
printf("the value is %d\n", val);
free(r) ;
k=1;
}
l=p;
printf("last data is:%d\n",p->data) ;
return l;
}
int main(){/*主函数*/
nodeptr l;
l=creat();/*创建循环单链表*/
out(l);/*输出*/
joseph(l);/*求解约瑟夫回环问题*/
return 0;
}
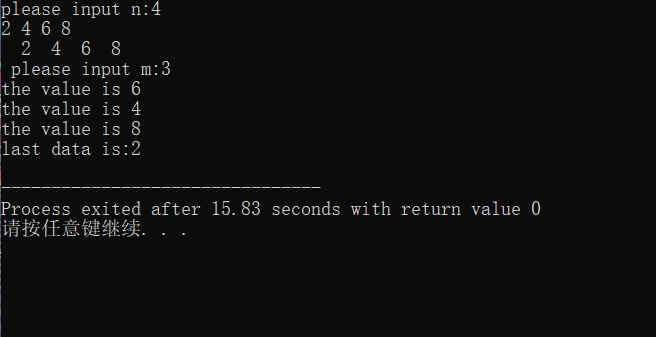
- 运行结果:
![]()
四、实验小结
该项实验主要编写了有关顺序表和链表的程序,进行了创建,初始化,输入,输出,插入,删除,查找多种功能的程序编写,了解并掌握了相关基本概念,在程序编写过程中会对顺序表与链表的原理有更深一步的了解。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号