图总结

图总结

思维导图

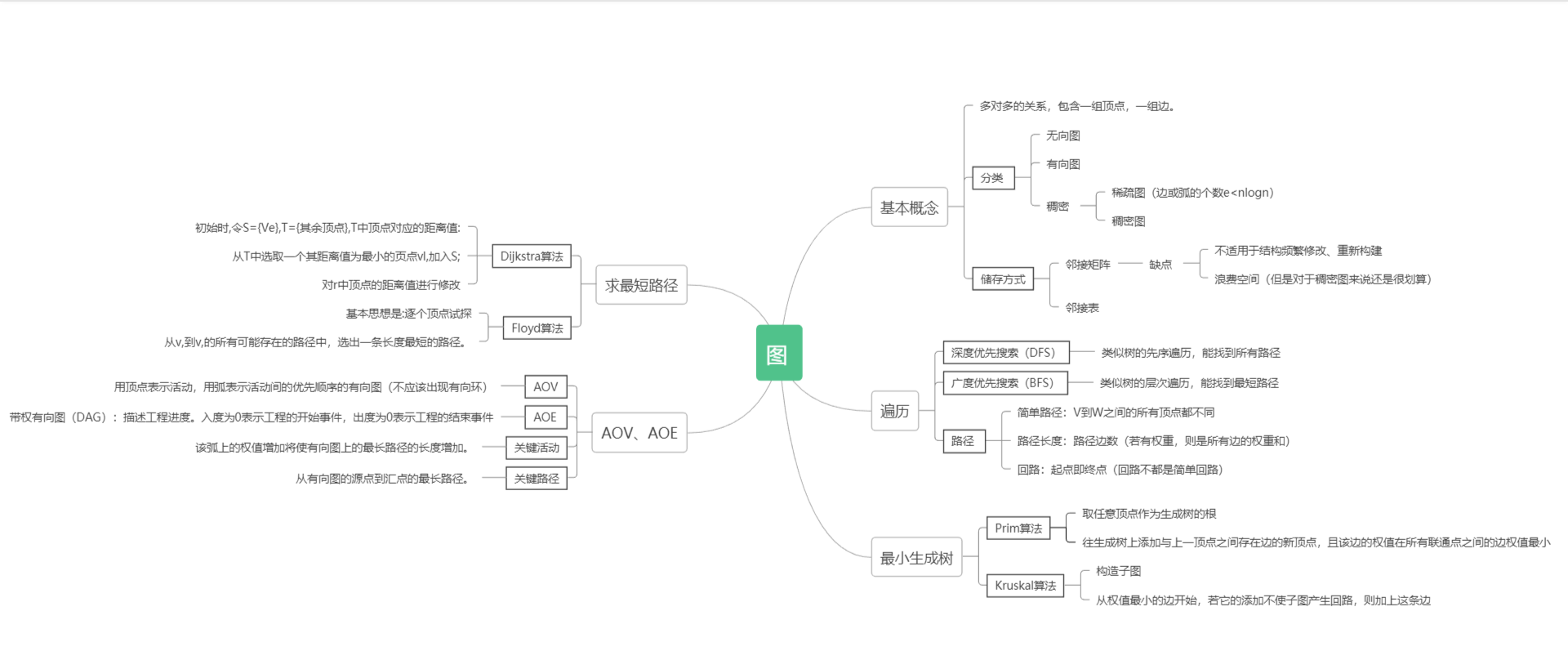
重要概念笔记

假设图中有n个顶点，e条边，则

1. 含有e n(n-1)2条边的无向图称作完全图;
2. 含有c-n(n-l)条弧的有向图称作有向完全图;
3. 若边或弧的个数e<nlogn，则称作稀疏图，否则称作稠密图。

遍历：

从给定图中任意指定的顶点(初始点)出发，按照某种搜索方法沿着图的边访问图中所有顶点，是每个顶点仅被访问一次。

深度优先搜索(DFS):

从图中某个初始顶点V出发 ，首先访问初始顶点V ，然后选择一个与顶点V相邻且没有被访问过的顶点W为初始顶点，再从W出发 ，进行深度优先搜索，直到途中与当前顶点邻接的所有顶点都被访问过为止。

广度优先搜索(BFS):

首先访问初始点Vi，接着访问Vi的所以未被访问过的邻接点Vi1，Vi2……，然后再按照Vi1，Vi2……的次序，访问每一个顶点的所有未被访问的邻接点，依次类推，直到图中所有和初始点Vi有路径相通的顶点都被访问过为止。

连通：

两顶点间有路径，称两顶点是连通的。

连通图：

图中任意两顶点均连通。

连通分量:无向图G的极大连通子图称为G的连通分量(Connected Component)。

注意:

1. 任何连通图的连通分量只有一个，即是其自身
2. 非连通的无向图有多个连通分量
3. 极大顶点数:再加1个顶点就不连通了
4. 极大边数:包含子图中所有顶点相连的所有边

Prim算法

1. 取任意顶点作为生成树的根
2. 往生成树上添加新顶点，新顶点与树上的顶点必定存在一条边，且该边的权值在所有联通点之间的边取值最小
3. 继续往生成树上添加顶点,直至加完。

克鲁斯卡尔(Kruskal)算法

考虑问题的出发点:为使生成树上边的权值之和达到最小。则应使生成树中每条边的权值尽可能地小。

Dijkstra算法

1. 图用带权邻接矩阵存储a[][];数组D[]存放当前战到的从源点ve到每个终点的最短路径长度，其初态为图中直接路径权值;
2. 数组Path[ ]表示从ve到各终点的最短路径上,此顶点的前一顶点的序号;若从Ve到某终点无路径,则用e作为其前一顶点的序号。(重点理解)

Floyd算法

1. 图用邻接矩阵存储;
2. 二维数组D[ ][ ]存放顶点对之间的最短路径长度;Path[i][j]是从vi到vj,的最短路径上vj前一顶点序号。

如何求关键活动