数据结构与算法笔记一：算法复杂度、栈、队列、链表

@

目录

• 一、算法概述、复杂度
  • 1.1算法的概念
  • 1.2算法效率衡量
    • 1.2.1执行时间反应算法效率
    • 1.2.2单靠时间值绝对可信吗？
    • 1.2.3 “大O记法”
    • 1.2.4如何理解“大O记法”
  • 1.3最坏时间复杂度
  • 1.4时间复杂度计算规则
  • 1.5 数据结构
  • 1.6算法与数据结构的区别
  • 1.7 demo：“变位词”判断问题
  • 1.8 list和dict时间复杂度
• 二、线性结构linear structure
• 三、 栈
  • 3.1 括号匹配
  • 3.2 进制转换
  • 3.3 表达式转换及求值
    • 3.3.1 通用的中缀转后缀算法
    • 3.3.2 后缀表达式求值
• 四、 队列
  • 4.1 热土豆（约瑟夫问题）
  • 4.2 打印任务
  • 4.3 双端队列
  • 4.4 回文词判定
• 五、链表
  • 5.1无序表（UnorderedList）
  • 5.2有序表OrderedList

一、算法概述、复杂度

1.1算法的概念

五大特性：输入、输出、有穷、确定、可行。

  算法是计算机处理信息的本质，因为计算机程序本质上是一个算法来告诉计算机确切的步骤来执行一个指定的任务。一般地，当算法在处理信息时，会从输入设备或数据的存储地址读取数据，把结果写入输出设备或某个存储地址供以后再调用。

  算法是独立存在的一种解决问题的方法和思想。 对于算法而言，实现的语言并不重要，重要的是思想。算法可以有不同的语言描述实现版本（如C描述、C++描述、Python描述等），本文使用Python语言进行描述实现。

1.2算法效率衡量

1.2.1执行时间反应算法效率

  对于同一问题，我们给出了两种解决算法，在两种算法的实现中，我们对程序执行的时间进行了测算，发现两段程序执行的时间相差悬殊（214.583347秒相比于0.182897秒），由此我们可以得出结论：实现算法程序的执行时间可以反应出算法的效率，即算法的优劣。

1.2.2单靠时间值绝对可信吗？

  假设我们将第二次尝试的算法程序运行在一台配置古老性能低下的计算机中，情况会如何？很可能运行的时间并不会比在我们的电脑中运行算法一的214.583347秒快多少。

  单纯依靠运行的时间来比较算法的优劣并不一定是客观准确的！。程序的运行离不开计算机环境（包括硬件和操作系统），这些客观原因会影响程序运行的速度并反应在程序的执行时间上。那么如何才能客观的评判一个算法的优劣呢？

• 一个算法所实施的操作数量或步骤数可作为独立于具体程序/机器的度量指标
  哪种操作跟算法的具体实现无关?需要一种通用的基本操作来作为运行步骤的计量单位
• 赋值语句是一个合适的选择
  一条赋值语句同时包含了(表达式)计算和(变量)存储两个基本资源。仔细观察程序设计语言特性，除了与计算资源无关的定义语句外，主要就是三种控制流语句和赋值语句，而控制流仅仅起了组织语句的作用，并不实施处理。

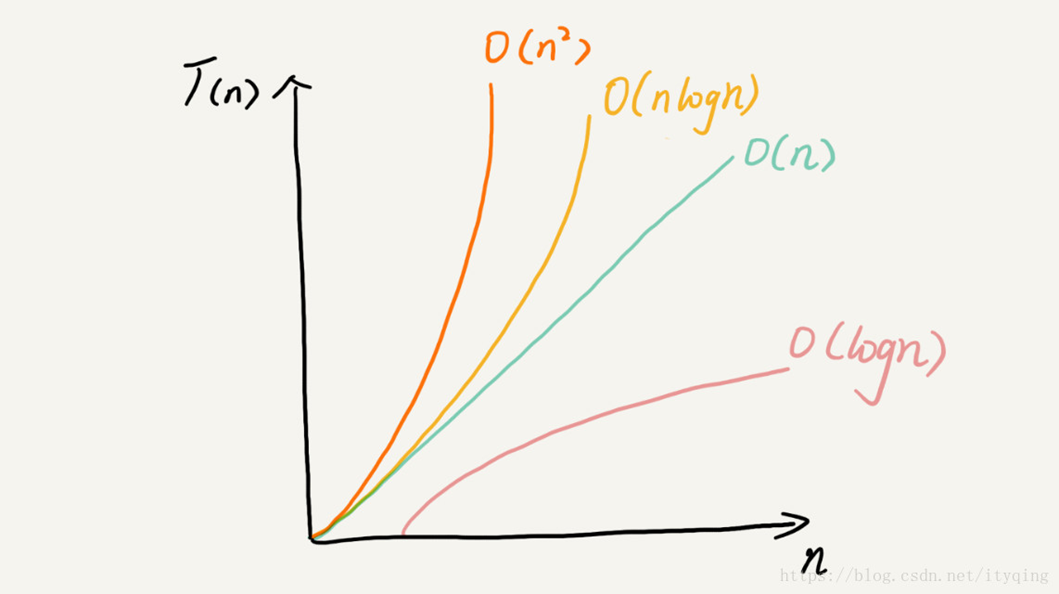
数量级函数 Order of Magnitude

• 基本操作数量函数T(n)的精确值并不是特别重要，重要的是T(n)中起决定性因素的主导部分
  用动态的眼光看，就是当问题规模增大的时候， T(n)中的一些部分会盖过其它部分的贡献
• 数量级函数描述了T(n)中随着n增加而增加速度最快的主导部分，称作“大O”表示法，记作O(f(n))，其中f(n)表示T(n)中的主导部分.

1.2.3 “大O记法”

  我们假定计算机执行算法每一个基本操作的时间是固定的一个时间单位，那么有多少个基本操作就代表会花费多少时间单位。算然对于不同的机器环境而言，确切的单位时间是不同的，但是对于算法进行多少个基本操作（即花费多少时间单位）在规模数量级上却是相同的，由此可以忽略机器环境的影响而客观的反应算法的时间效率。

  对于算法的时间效率，我们可以用“大O记法”来表示。

  “大O记法”：对于单调的整数函数f，如果存在一个整数函数g和实常数c>0，使得对于充分大的n总有f(n)<=c*g(n)，就说函数g是f的一个渐近函数（忽略常数），记为f(n)=O(g(n))。也就是说，在趋向无穷的极限意义下，函数f的增长速度受到函数g的约束，亦即函数f与函数g的特征相似。*

时间复杂度：假设存在函数g，使得算法A处理规模为n的问题示例所用时间为T(n)=O(g(n))，则称O(g(n))为算法A的渐近时间复杂度，简称时间复杂度记为T(n)。

影响算法运行时间的其它因素：

• 有时决定运行时间的不仅是问题规模
• 某些具体数据也会影响算法运行时间。比如算法分为最好、最差和平均情况，平均状况体现了算法的主流性能。对算法的分析要看主流，而不被某几种特定的运行状况所迷惑。

1.2.4如何理解“大O记法”

  对于算法进行特别具体的细致分析虽然很好，但在实践中的实际价值有限。对于算法的时间性质和空间性质，最重要的是其数量级和趋势，这些是分析算法效率的主要部分。而计量算法基本操作数量的规模函数中那些常量因子可以忽略不计。例如，可以认为3n2和100n2属于同一个量级，如果两个算法处理同样规模实例的代价分别为这两个函数，就认为它们的效率“差不多”，都为n2级。

1.3最坏时间复杂度

分析算法时，存在几种可能的考虑：

• 算法完成工作最少需要多少基本操作，即最优时间复杂度
• 算法完成工作最多需要多少基本操作，即最坏时间复杂度
• 算法完成工作平均需要多少基本操作，即平均时间复杂度

1. 对于最优时间复杂度，其价值不大，因为它没有提供什么有用信息，其反映的只是最乐观最理想的情况，没有参考价值。
2. 对于最坏时间复杂度，提供了一种保证，表明算法在此种程度的基本操作中一定能完成工作。
3. 对于平均时间复杂度，是对算法的一个全面评价，因此它完整全面的反映了这个算法的性质。但另一方面，这种衡量并没有保证，不是每个计算都能在这个基本操作内完成。而且，对于平均情况的计算，也会因为应用算法的实例分布可能并不均匀而难以计算。

因此，我们主要关注算法的最坏情况，亦即最坏时间复杂度。

1.4时间复杂度计算规则

1. 基本操作，即只有常数项，认为其时间复杂度为O(1)
2. 顺序结构，时间复杂度按加法进行计算
3. 循环结构，时间复杂度按乘法进行计算
4. 分支结构，时间复杂度取最大值
5. 判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略
6. 在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度

1.5 数据结构

  数据是一个抽象的概念，将其进行分类后得到程序设计语言中的基本类型。如：int，float，char等。数据元素之间不是独立的，存在特定的关系，这些关系便是结构。数据结构指数据对象中数据元素之间的关系。

  Python给我们提供了很多现成的数据结构类型，这些系统自己定义好的，不需要我们自己去定义的数据结构叫做Python的内置数据结构，比如列表、元组、字典。而有些数据组织方式，Python系统里面没有直接定义，需要我们自己去定义实现这些数据的组织方式，这些数据组织方式称之为Python的扩展数据结构，比如栈，队列等。

1.6算法与数据结构的区别

程序 = 数据结构 + 算法
  数据结构只是静态的描述了数据元素之间的关系。高效的程序需要在数据结构的基础上设计和选择算法。

总结：算法是为了解决实际问题而设计的，数据结构是算法需要处理的问题载体

1.7 demo：“变位词”判断问题

• 问题描述：变位词是指两个词之间存在组成字母的重新排列关系。如heart和earth，python和typhon。为了简单起见，假设参与判断的两个词仅由小写字母构成，且长度相等。

• 解题目标：写一个bool函数，以两个词作为参数，返回这两个词是否为变位词。

解法一：逐字检查

• 解法思路：将词1中的字符逐个到词2检查是否存在，存在就打勾标记（防止重复检查），如果每个字符都能找到，则两个词是变位词，只要有一个字符找不到，就不是变位词。

• 程序技巧：实现打勾标记：将词2对应字符设为None，由于字符串是不可变类型，需要先复制到列表中。（列表才是可以修改的）

• 代码实现：

def anangramSolution1(s1,s2):
    alist = list(s2)
    pos1 = 0
    stillOK = True
    while pos1 < len(s1) and stillOK:
        pos2 = 0
        found = False
        while pos2 < len(alist) and not found:
            if s1[pos1] == alist[pos2]:
                found = True
            else:
                pos2 = pos2 + 1
        if found:
            alist[pos2] = None
        else:
            stillOK = False
        pos1 = pos1 + 1
    return stillOK
print(anangramSolution1('heart','earth'))

• 代码时间复杂度：总执行次数为：1+2+3+…+n ，故时间复杂度为：O(n²)

解法二：排序比较

• 解法思路：将两个字符串都按照字母顺序排好序，再逐个字符对比是否相同，如果相同则是变位词，有任何不同则不是变位词。

• 代码实现：

def anagramSolution2(s1,s2):
    alist1 = list(s1)
    alist2 = list(s2)
    alist1.sort()
    alist2.sort()
    pos = 0
    matches = True
    while pos < len(s1) and matches:
        if alist1[pos] == alist2[pos]:
            pos = pos + 1
        else:
            matches = False
    return matches
print(anagramSolution2('heart','earth'))

• 代码时间复杂度：本算法时间主导的步骤是排序步骤，所以时间复杂度就等于排序的时间复杂度：O(nlogn)

解法三：计数比较

• 解法思路：对比两个词中每个字母出现的次数，如果26个字母出现次数都相同的话，这两个字符串就一定是变位词。

• 具体做法：为每个词设置一个26位计数器，先检查每个词，在计数器中设定好每个字母出现的次数。计数完成后，进入比较阶段，看两个字符串的计数器是否相同，如果相同则说明是变位词。

• 代码实现：

def anagramSolution3(s1,s2):
    c1 = [0] * 26
    c2 = [0] * 26
    for i in range(len(s1)):
        pos = ord(s1[i]) - ord('a') # ord()返回一个字母的unicode编码
        c1[pos] = c1[pos] + 1
    for i in range(len(s2)):
        pos = ord(s2[i]) - ord('a')
        c2[pos] = c2[pos] + 1
    j = 0
    stillOK = True
    while j < 26 and stillOK:
        if c1[j] == c2[j]:
            j = j + 1
        else:
            stillOK = False
return stillOK
print(anagramSolution3('heart','earth'))

• 代码时间复杂度：前两个循环用于对字符串进行计数，操作次数等于字符串长度n，第三个循环用于计数器比较，操作次数为26。所以该代码总操作次数为：2n+26，时间复杂度为：O(n)

  注：该代码也采用了 “用空间换时间” 的思想。因为两次统计词频存储了两个变量。如果是大字符集会要求更多的存储空间。

方法四：穷举法

  穷举str1的所有字母组合可能，看str2在不在str1的所有组合排列里面。str1的穷举组合可能性为n！，比2n还大。当n=20的时候，每微秒处理一个组合要8万年。

1.8 list和dict时间复杂度

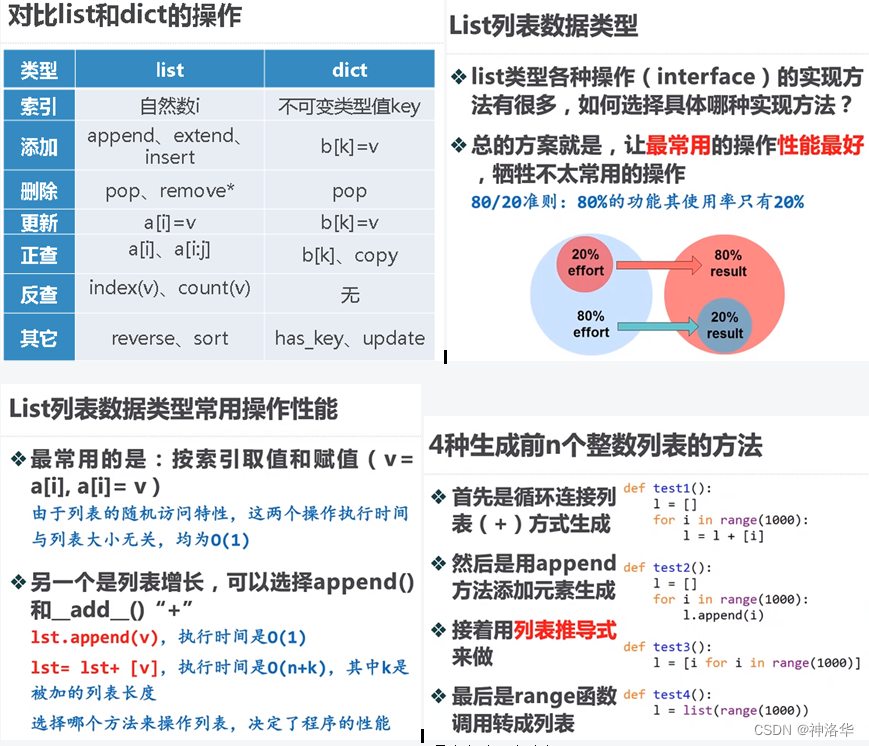
  mian是主程序运行空间，number是程序执行次数，运行时间分别是1.889、0.0915、0.0384、0.0097。

pop()是删除最后一个元素，pop（i）是删除第i元素。

二、线性结构linear structure

线性结构是一种有序数据项的集合，任何两个数据项只有先后的关系。其中每个数据项都有唯一的前驱和后继。

• 除了第一个没有前驱，最后一个没有后继。
• 新的数据项加入到数据集中时，只会加入到原有某个数据项之前或之后。
• 具有这种性质的数据集，就称为线性结构。

1. 四个线性结构

• 栈 stack —— 后进先出（LIFO：last in first out）
• 队列 queue —— 先进先出（FIFO：first in first out）（计算机进程队列、消息队列）
• 双端队列 deque
• 列表 list

类比于浏览器的后退或者word的撤销。

三、 栈

3.1 括号匹配

from pythonds.basic.stack import Stack
def parChecker(symbolString):
    s = Stack()
    balanced = True
    index = 0
    while index < len(symbolString) and balanced:
        symbol = symbolString[index]
        if symbol == "(":
            s.push(symbol)
        else:
            if s.isEmpty():
                balanced = False
            else:
                s.pop()
        index = index + 1
 
    if balanced and s.isEmpty():
        return True
    else:
        return False
 
print(parChecker('((()))'))
print(parChecker('(()'))

3.2 进制转换

多少进制就是多少进制的几次幂

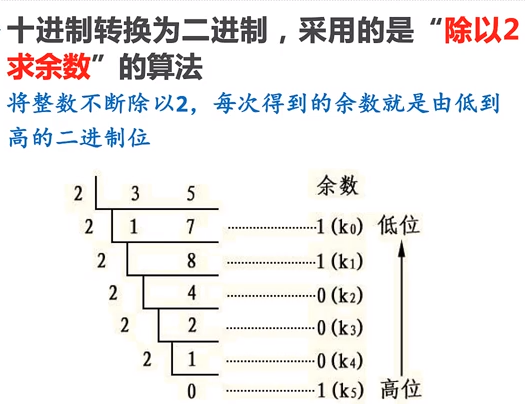
from pythonds.basic.stack import Stack
def baseConverter(decNumber,base):
    digits = "0123456789ABCDEF"
    remstack = Stack()
    while decNumber > 0:
        rem = decNumber % base
        remstack.push(rem)
        decNumber = decNumber // base
    newString = ""
    while not remstack.isEmpty():
        newString = newString + digits[remstack.pop()]
    return newString
print(baseConverter(25,2))
print(baseConverter(25,16))

3.3 表达式转换及求值

• 中缀表达式
  • 中缀表达式：操作符介于操作数之间的表达式。
  • 中缀(infix)表达式：A + B * C + D ，为了避免计算顺序混淆，引入全括号表达式；
  • 全括号中缀表达式：((A + (B * C)) + D)，内层括号优先级更高。
• 前缀和后缀表达式
  • 前缀(prefix)表达式：将操作符移到前面，形式变为：操作符、第一操作数、第二操作数。
  • 后缀(postfix)表达式：将操作符移到后面，形式变为：第一操作数、第二操作数、操作符。

1. 中缀转换为前缀/后缀表达式

例：(A + (B * C))

• 把操作符移到子表达式(B * C)的右括号位置替代它，再删去左括号得到BC，接着把操作符+移到相应的右括号并删掉左括号，表达式就转为 后缀 形式，即：ABC*+ 。
• 前后缀表达式中，操作符顺序完全决定了运算的次序，多数情况下计算机用此方法，特别是后缀法。
• 离操作数越近的越先做
• 同理，把操作符移到相应的左括号替代之，并删掉右括号，表达时就转换为 前缀 形式，即：+A*BC 。
• 总结：无论表达式多复杂，转换为前缀或后缀只需要两个步骤：
  (1) 将中缀表达式转换为全括号形式；
  (2) 将所有操作符移动到子表达式所在的左括号（前缀）或者右括号（后缀）处，替代之，再删除所有括号。

3.3.1 通用的中缀转后缀算法

• 在中缀表达式转换为后缀形式的处理过程中，操作符比操作数要晚输出，所以在扫描到对应的第二个操作数之前，需要把操作符先保存起来；
• 而这些暂存的操作符，由于优先级的规则还有可能要反转次序输出。
  在A+B*C中，+虽然先出现，但优先级比后面这个*要低，所以它要等*处理完后，才能再处理。
• 这种反转特性，使得我们考虑用栈来保存暂时未处理的操作符。

  总结下，在从左到右扫描逐个字符扫描中缀表达式的过程中，采用一个栈来暂存未处理的操作符。这样，栈顶的操作符就是最近暂存进去的，当遇到一个新的操作符，就需要跟栈顶的操作符比较下优先级，再行处理。
  所以遇到左括号，要标记下，其后出现的操作符优先级提升了，一旦扫描到对应的右括号，就可以马上输出这个操作符

流程：

• 从左到右扫描中缀表达式单词列表，如果单词是操作数，则直接添加到后缀表达式列表的末尾；如果单词是左括号，则压入opstack栈顶；如果单词是右括号，则反复弹出opstack栈顶操作符，加入到输出列表末尾，直到碰到左括号；如果单词是操作符，则压入opstack栈顶，但在压入栈顶之前，要比较其与栈顶操作符的优先级，如果栈顶的高于或等于它，就要反复弹出栈顶操作符，加入到输出列表末尾；直到栈顶的操作符优先级低于它。
• 中缀表达式单词列表扫描结束后，把opstack栈中的所有剩余操作符
  依次弹出，添加到输出列表末尾。
• 把输出列表再用join方法合并成后缀表达式字符串，算法结束。

代码实现：

from pythonds.basic.stack import Stack

def infixToPostfix(infixexpr):
    prec = {}
    prec["*"] = 3
    prec["/"] = 3
    prec["+"] = 2
    prec["-"] = 2
    prec["("] = 1
    opStack = Stack()
    postfixList = []
    tokenList = infixexpr.split()

    for token in tokenList:
        if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":
            postfixList.append(token)
        elif token == '(':
            opStack.push(token)
        elif token == ')':
            topToken = opStack.pop()
            while topToken != '(':
                postfixList.append(topToken)
                topToken = opStack.pop()
        else:
            while (not opStack.isEmpty()) and \
                (prec[opStack.peek()] >= prec[token]):
                postfixList.append(opStack.pop())
            opStack.push(token)
    while not opStack.isEmpty():
        postfixList.append(opStack.pop())
    return " ".join(postfixList)

3.3.2 后缀表达式求值

流程：

• 创建空栈operandStack用于暂存操作数。
• 将后缀表达式用split方法解析为单词（token）的列表。
• 从左到右扫描单词列表，如果单词是一个操作数，将单词转换为整数int，压入operandStack栈顶；如果单词是一个操作符，就开始求值，从栈顶弹出两个操作数，先弹出的是右操作数，后弹出的是左操作数，计算后将值重新压入栈顶。
• 单词列表扫描结束后，表达式的值就在栈顶。
• 弹出栈顶的值，返回。

代码实现：

from pythonds.basic.stack import Stack

def postfixEval(postfixExpr):
    operandStack = Stack()
    tokenList = postfixExpr.split()

    for token in tokenList:
        if token in "0123456789":
            operandStack.push(int(token))
        else:
            operand2 = operandStack.pop()
            operand1 = operandStack.pop()
            result = doMath(token,operand1,operand2)
            operandStack.push(result)
    return operandStack.pop()

def doMath(op,op1,op2):
    if op == "*":
        return op1 * op2
    elif op == "/":
        return op1 / op2
    elif op == "+":
        return op1 + op2
    else:
        return op1 - op2

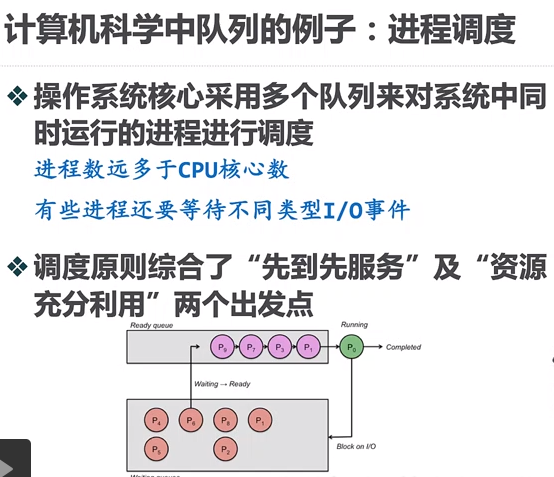
四、 队列

打印机打印任务和系统进程服务调度

4.1 热土豆（约瑟夫问题）

流程：

• 用队列来实现热土豆问题的算法，参加游戏的人名列表，以及传土豆次数num，算法返回最后剩下的人名。
• 采用队列存放参加游戏的人名，按照传递土豆方向从队首排到队尾，游戏时，队首始终是持有土豆的人。
• 游戏开始，只需要将队首的人出队，随即再到队尾入队，算是土豆的一次传递，传递了num次后，将队首的人移除，不再入队，如此反复，直到队里剩余1个人。

代码实现：

from pythonds.basic.queue import Queue

def hotPotato(namelist,num):
    simqueue = Queue()
    for name in namelist:
        simqueue.enqueue(name)

    while simqueue.size() > 1:
        for i in range(num):
            simqueue.enqueue(simqueue.dequeue())#一次传递
        simqueue.dequeue()#返回最后一个人

    return simqueue.dequeue()
# 从1数到5，第五个人出列
print(hotPotato(["A","B","C","D","E","F","G"],4))

4.2 打印任务

  打印任务具体实例配置如下：一个实验室，在任意的一个小时内，大约有10名学生在场，这一小时中，每人会发起两次打印任务，每次1-20页。

   打印机的性能是：以草稿模式打印的话，每分钟10页；以正常模式打印的话，打印质量好，但速度下降为每分钟5页。

  决策支持：找到一个让大家都不会等太久，又能尽量提高打印质量。

问题建模：

• 对象：打印任务、打印队列、打印机
  打印任务的属性：提交时间，打印页数
  打印队列的属性：具有FIFO性质的打印任务队列
  打印机的属性：打印速度，是否在忙
• 过程：生成和提交打印任务：
  确定生成概率：每180秒会有一个作业生成并提交，概率为每秒1/180
  确定打印页数：实例是1-20页，也就是1-20页之间概率相同
• 过程：实施打印：
  当前打印就是正在打印的作业
  新作业开始打印时开始倒计时，回0表示打印完毕，可以处理下一个作业
• 模拟时间：
  统一的时间框架：以秒均匀流逝的时间，设定结束时间
  同步所有过程：在一个时间单位里，对生成打印任务和实施打印两个过程各处理一次

模拟流程：

• 创建打印队列对象。
• 时间按照秒的单位流逝。按照概率生成打印作业，加入打印队列；如果打印机空闲且队列不空，则取出队首作业打印，记录此作业等待时间；如果打印机忙，则按照打印速度进行1秒打印；如果当前作业打印完成，则打印机进入空闲。
• 时间用尽，开始统计平均等待时间。

代码实现：

from pythonds.basic.queue import Queue
import random

class Printer:
    def __init__(self,ppm):
        self.pagerate = ppm # 打印速度
        self.currentTask = None # 当前打印任务，None为空闲
        self.timeRemaining = 0  # 任务倒计时，当前打印任务还剩多少时间

    def tick(self):  # 打印1秒
        if self.currentTask != None:#当前有任务
            self.timeRemaining = self.timeRemaining -1#打印倒计时减一
            if self.timeRemaining <= 0:
                self.currentTask = None

    def busy(self):  # 打印是否忙
        if self.currentTask != None:
            return True
        else:
            return False

    def startNext(self,newtask):  # 开始打印新作业，传入打印作业对象
        self.currentTask = newtask#当前打印作业设置成打印对象
        self.timeRemaining = newtask.getPages()*60/self.pagerate#计算打印时间

class Task:#打印任务
    def __init__(self,time):
        self.timestamp = time  # 生成时间戳
        self.pages = random.randrange(1,21)  # 打印页数

    def getStamp(self):
        return self.timestamp #生成时间戳

    def getPages(self):
        return self.pages #返回页数

    def waitTime(self,currenttime):
        return currenttime - self.timestamp  # 等待时间

def newPrintTask():#新生成打印作业，布尔函数
    num = random.randrange(1,181)  # 1/180概率生成作业
    if num == 180:
        return True
    else:
        return False

def simulation(numSeconds,pagesPerMinute):#模拟时间和打印机的模式
    labprinter = Printer(pagesPerMinute)#生成打印机对象
    printQueue = Queue()#准备打印队列
    waitingtimes = []#生成等待时间列表，以便记录

    for currentSecond in range(numSeconds):
        if newPrintTask():#如果1/180概率生成打印作业
            task = Task(currentSecond)#创建新的task打印对象，传递生成时间
            printQueue.enqueue(task)#新的打印任务传入打印队列

        if (not labprinter.busy()) and (not printQueue.isEmpty()):#如果打印机空闲并且队列有打印任务
            nexttask = printQueue.dequeue()#取出打印任务并打印一秒
            waitingtimes.append(nexttask.waitTime(currentSecond))#开始打印时就可以计算当前打印任务的等待时间，加入等待时间列表
            labprinter.startNext(nexttask)#开始打印

        labprinter.tick()#打印一秒

    averageWait = sum(waitingtimes)/len(waitingtimes)
    print("Average Wait %6.2f secs %3d tasks remaining." \
                %(averageWait,printQueue.size()))#输出截止时间还有几个作业没打印完

for i in range(20):
    simulation(3600,5)

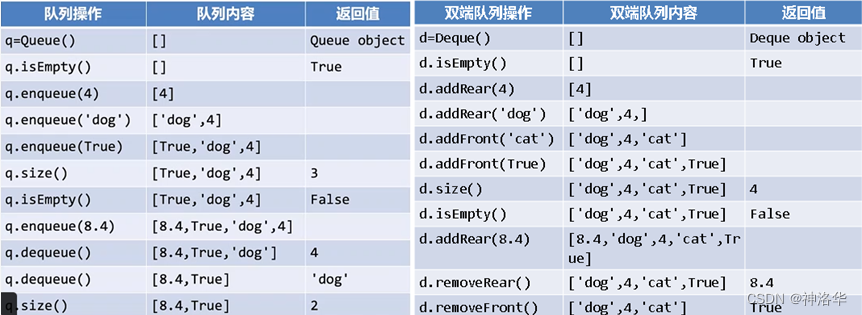
4.3 双端队列

• 双端队列是一种有次序的数据集，数据项既可以从队首加入，也可以从队尾加入，数据项也可以从两端删除；某种意义上说，双端队列集成了栈和队列的能力。
• 但双端队列并不具有内在的LIFO和FIFO特性，如果用双端队列来模拟栈和队列，需要由使用者自行维护操作的一致性。

4.4 回文词判定

  用双端队列很容易解决回文词问题，先将需要判定的词从队尾加入deque，再从两端同时移除字符判定是否相同，直到deque中剩下0个或1个字符。

实现代码：

from pythonds.basic.deque import Deque

def palchecker(aString):
    chardeque = Deque()

    for ch in aString:
        chardeque.addRear(ch)

    stillEqual = True
    while chardeque.size() > 1 and stillEqual:
        first = chardeque.removeFront()
        last = chardeque.removeRear()
        if first != last:
            stillEqual = False
    return stillEqual

print(palchecker("lsdkjfskf"))
print(palchecker("radar"))

五、链表

5.1无序表（UnorderedList）

• 虽然列表数据结构要求保持数据项的前后相对位置，但这种前后位置的保持，并不要求数据项依次存放在连续的存储空间。如下图，数据项存放位置并没有规则，但如果在数据项之间建立链接指向，就可以保持其前后相对位置。第一个和最后一个数据项需要显示标记出来，一个是队首，一个是队尾，后面再无数据了。
• 插入删除元素时需要移动表中元素，而不是修改指针，顺序表也是随机存取数据。

1. 链表实现：节点Node

• 链表实现的最基本元素是节点Node，每个节点至少要包含两个信息：数据项本身、以及指向下一个节点的引用信息。注意next为None的意义是没有下一个节点了。

2. 链表实现：无序表UnorderedList

• 可以采用链接节点的方式构建数据集来实现无序表。
• 链表的第一个和最后一个节点最重要。如果想访问到链表中的所有节点，就必须从一个节点开始沿着链接遍历下去。
• 所以无序表必须要有对第一个节点的引用信息，设立一个属性head，保存对第一个节点的引用，空表的head为None。
• 随着数据项的加入，无序表的head始终指向链条的第一个节点，无序表mylist对象本身并不包含数据项（数据项在节点中）。其中包含的head只是对首个节点Node的引用，判断空表的isEmpty()很容易实现。
• 无序表实现add方法，按照实现的性能考虑，应该添加到最容易加入的位置上，也就是表头，整个链表的首位置。
  

3. 链表实现：size

• 从链表头head开始遍历到表尾同时用变量累加经过的节点个数(只要节点不是None)，复杂度O(n)

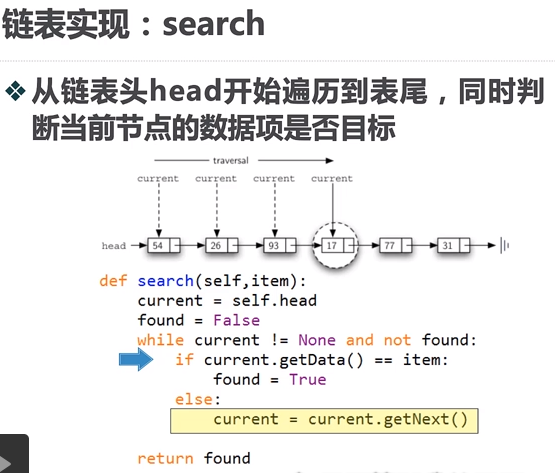
4. 链表实现：search

• 从链表头head开始遍历到表尾，同时判断当前节点的数据项是否为目标。

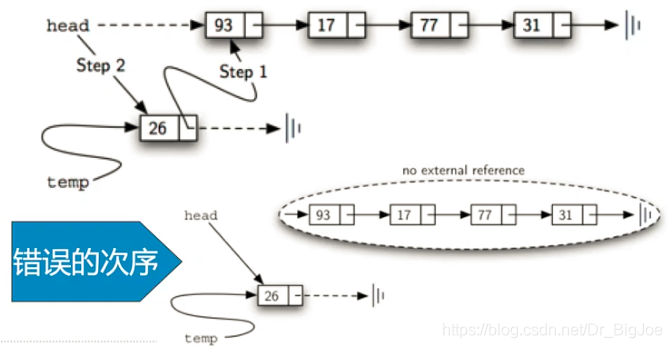
5. 链表实现：remove(item)方法

• 首先找到item，这个过程和search一样，但删除节点时，需要特别的技巧。
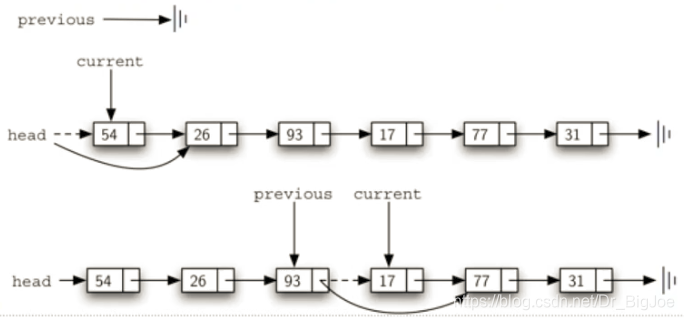
• current指向的是当前匹配数据项的节点，而删除需要把前一个节点的next指向current的下一个节点，所以我们在查找current的同时，还要维护前一个(previous)节点的引用。
  
• 找到item后，current指向item节点，previous指向前一个节点，开始执行删除，需要区分两种情况：current是首个节点；或者是位于链条中间的节点。
  

代码实现：

class Node:
    def __init__(self,initdata):
        self.data = initdata
        self.next = None

    def getData(self):
        return self.data

    def getNext(self):
        return self.next

    def setData(self,newdata):
        self.data = newdata

    def setNext(self,newnext):
        self.next = newnext

class UnorderedList:
    def __init__(self):
        self.head = None

    def add(self,item):
        temp = Node(item)
        temp.setNext(self.head)
        self.head = temp

    def size(self):
        current = self.head
        count = 0
        while current != None:
            count = count + 1
            current = current.getNext()
        return count

    def search(self,item):
        current = self.head
        found = False
        while current != None and not found:
            if current.getData() == item:
                found = True
            else:
                current = current.getNext()
        return found

    def remove(self,item):
        current = self.head
        previous = None
        found = False
        while not found:
            if current.getData() == item:
                found = True
            else:
                previous = current
                current = current.getNext()
        if previous == None:
            self.head = current.getNext()
        else:
            previous.setNext(current.getNext())

5.2有序表OrderedList

• 在实现有序表时，需要记住数据项的相对位置，取决于他们之间的“大小”比较，Node定义相同，OrderedList也设置一个head来保存链表表头的引用。
• 对于isEmpty()，size()，remove()方法与节点次序无关，其实现与UnorderedList相同。
• search和add方法需要修改。

有序表实现：search方法

• 在无序表的search中，如果需要查找的数据项不存在，则会搜遍整个链表，直到表尾。
• 对于有序表来说，可以利用链表节点有序排列的特性，来为search节省不存在数据项的查找时间。一旦当前节点的数据项大于所要查找的数据项，则说明链表后面已经不可能再有要查找的数据项，可以直接返回False。
• add方法必须保证加入的数据项添加在合适的位置，以维护整个链表的有序性。
• 从头找到第一个比添加项大的数据项，将添加项插到该数据项前面。
• 跟remove方法类似，引入一个previous，跟随当前节点current。

代码实现：

class Node:
    def __init__(self,initdata):
        self.data = initdata
        self.next = None

    def getData(self):
        return self.data

    def getNext(self):
        return self.next

    def setData(self,newdata):
        self.data = newdata

    def setNext(self,newnext):
        self.next = newnext

class OrderedList:
    def __init__(self):
        self.head = None

    def search(self,item):
        current = self.head
        found = False
        stop = False
        while current != None and not found and not stop:
            if current.getData() == item:
                found = True
            else:
                if current.getData() > item:
                    stop = True
                else:
                    current = current.getNext()
        return found

    def add(self,item):
        current = self.head
        previous = None
        stop = False
        while current != None and not stop:
            if current.getData() > item:
                stop = True
            else:
                previous = current
                current = current.getNext()
        temp = Node(item)
        if previous == None:
            temp.setNext(self.head)
            self.head = temp
        else:
            temp.setNext(current)
            previous.setNext(temp)