高等数学A2 2020/6/9 第三十次课
返回主索引
对坐标的曲线积分
定义&形式
曲面是有方向的，要提前判断正负
组合形式 \(\iint\limits_\sum P(x,y,z)dydz+Q(x,y,z)dzdx+R(x,y,z)dxdy\)
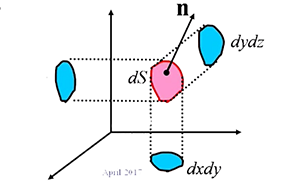
\(dS=(dydz,dzdx,dxdy)=\vec ndS=(cos\alpha dS,cos\beta dS,cos \gamma ds)\)
\(\vec{n}\) 与坐标轴的夹角为正即正投影，为负即为负投影
物理意义
流量场 \(V=(x,y,z)=P\vec i +Q\vec j+R\vec k\) 在单位时间流过曲面 \(\sum\) 的流量 $\Phi $
\(\Phi = \iint\limits_{\sum}Pdydz+Qdzdx+Rdxdy=\iint\limits_{\sum}(pcos\alpha +Qcos\beta +Rcos\gamma )dS\)
物理解释：流过曲面的流量
计算方法
将第二类曲面积分直接化成二重积分（证明过程略）
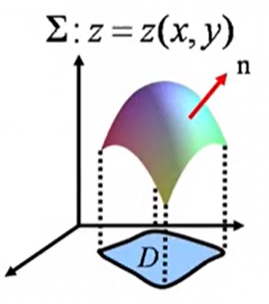
\(\iint\limits_{\sum }R(x,y,z)dxdy=\iint\limits_{D}R(x,y,z(x,y))dxdy\) （上侧）
\(\iint\limits_{\sum }R(x,y,z)dxdy=-\iint\limits_{D}R(x,y,z(x,y))dxdy\) （下侧）
特殊地，若曲面垂直于 \(XOy\) 坐标面，则对坐标 \(x,y\) 的曲面积分等于零
一般性质
若 \(\sum = \sum_1 + \sum_2\)
\(\iint\limits_{\sum }A·dS=\iint\limits_{\sum_1}AdS+\iint\limits_{\sum_2}A·dS\)
\(\iint\limits_{-\sum}A·dS=-\iint\limits_{\sum }A·dS\)
三合一公式
当 \(\sum:z=z(x,y)\;,\;(x,y)∈D\) 时，我们有以下公式：
\(\iint\limits_{\sum }Pdydz+Qdzdx+Rdxdy=\pm \iint\limits_{D}\{P,Q,R\}·\{-\frac{∂z}{∂x},\frac{∂z}{∂y},1\}dxdy\)
\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\pm \iint\limits_{D}(-P\frac{∂z}{∂x}-Q\frac{∂z}{∂y}+R)dxdy\)
\(\sum\) 取上（下）侧时，取正（负）号
