高等数学A2 2020/6/4 第二十九次课

返回主索引

对面积的曲面积分

定义

\(\iint\limits_{\sum}f(x,y,z)ds=\lim\limits_{\lambda\to 0}\sum\limits_{i=1}^{n}f(\xi _i,\eta _i,\zeta _i)\Delta S_i\)

物理意义：有质曲面的质量 \(M=\lim\limits_{\lambda\to 0}\sum\limits_{i=1}^{n}\mu (\xi _i,\eta _i,\zeta _i)\Delta S_i\)

其中 \(\mu (\xi _i,\eta _i,\zeta _i)\) 是面密度

\(\iint\limits_{\sigma }dS=S=\) 曲面的面积

计算方法

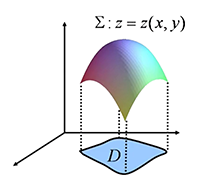
化为二重积分（以在 \(xOy\) 面上的投影为例，其余投影面同理）

\(\sum :z=z(x,y)\;\;(x,y)∈D\)

则 \(\iint\limits_{\sum }f(x,y,z)dS=\iint\limits_Df[x,y,z(x,y)]\sqrt{1+Z_x^2+Z_y^2}dxdy\)

其中 \(dS=\sqrt{1+Z_x^2+Z_y^2}dxdy\) 是面积元素

其余运算性质与定积分类似，在此不做赘述

利用对成型化简曲面积分

若 \(\sum\) 关于 \(XOy\) 面 \((z=0)\) 对称，则：

\(\iint\limits_{\sum }f(x,y,z)dS=\begin{cases}0\;\;\;\;当\;f(x,yz)\;关于\;z\;为奇函数\\2\iint\limits_{\sum }f(x,y,z)dS\;\;\;\;当\;f(x,y,z)\;关于\;z\;为偶函数\end{cases}\)

\(f(x,y,z)\) 关于 \(z\) 为奇函数：\(f(x,y,-z)\equiv -f(x,y,z)\)

\(f(x,y,z)\) 关于 \(z\) 为偶函数：\(f(x,y,-z)\equiv f(x,y,z)\)

\(\sum_1=\{(x,y,z)∈\sum |z\ge 0\}\)

若 \(\sum\) 关于其他坐标面堆成，也有相应的性质

曲面关于变量的轮换对称性

若 \((x,y,z)∈\sum\) 则将 \(x,y,z\) 任意互换的点也属于 \(\sum\)，则被积函数的自变量可以任意轮换而不会改变积分值

即：\(\iint\limits_{\sum }f(x,y,z)dS=\iint\limits_{\sum }f(y,x,z)dS=\iint\limits_{\sum }f(z,x,y)dS\)