高等数学A2 2020/5/26 第二十六次课

返回主索引

曲线积分与曲面积分

对弧长的曲线积分

积分形式

\(\lim\limits_{\lambda\to 0}\sum\limits_{i=1}^{n}f(\xi_i,\eta_i)\Delta s_i=\int\limits_l f(x,y)ds\)

空间曲线上对弧长的曲线积分：\(\int\limits_{l}f(x,y,z)ds=\lim\limits_{\lambda\to 0}\sum\limits_{i=1}^{n}f(\xi_i,\eta_i,\zeta_i)\Delta s_i\)

几何意义

若 \(f\) 为曲弧上点的线密度，则对弧长的曲线积分为曲线的质量

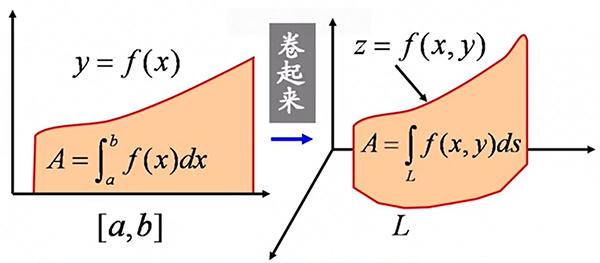
若 \(f\) 为与 \(l\) 一致，则对弧长的曲线积分为该曲线下方的柱面的面积

计算方法

设 \(f(x,y)\) 在曲线弧 \(l\) 上有定义且连续，\(l\) 的参数方程为 \(\begin{cases}x=\varphi (t)\\y=\psi (t)\end{cases}\;\;(\alpha\le t\le \beta)\)，

其中 \(\varphi (t),\phi (t)\) 在 \([\alpha,\beta ]\) 上具有一阶连续导数存在，且 \(\int\limits_l f(x,y)ds=\int_{\alpha}^{\beta}f[\varphi(t),\phi (t)]ds=\int_{\alpha}^{\beta}f[\varphi(t),\phi (t)]\sqrt{\varphi '(t)^2+\phi '(t)^2}dt\)

特殊地，当 \(f=1\) 时，即计算弧长

若 \(l\) 由极坐标给出，\(\rho =\rho (\theta )\;\;(\alpha\le\theta\le\beta)\)

则 \(ds=\sqrt{[\rho (\theta )]^2 +[\rho '(\theta)]^2}d\theta\)，\(\int\limits_l f(x,y)ds=\int^{\beta}_{\alpha}f[\rho (\theta)cos\theta ,\rho (\theta)sin\theta]\)