高等数学A2 2020/4/28 第十九次课

返回主索引

多元函数的极值及其求法

（以二元函数为例，其他多元函数同理）

极值的必要条件

设 \(z=f(x,y)\) 在点 \((x_0,y_0)\) 处取极值，且偏导数 \(f_x(x_0,y_0), f_y(x_0,y_0)\) 存在，

则 \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\)，根据曲面切平面的计算公式，

曲面 \(z=f(x,y)\) 在点 \((x_0,y_0,z_0)\) 有水平切平面 \(z=f(x_0,y_0)\)

多元函数取得极值的必要条件：梯度为零向量

多元函数的驻点 \((stationary\;point)\)

定义：多元函数定义域内梯度为零向量的点，有偏导数的极值点必为驻点，但是：

\((1)\) 驻点不一定是极值点，例如：\(z=xy\)

\((2)\) 极值点不一定是驻点，例如：\(z=\sqrt{x^2+y^2}\)

极值的充分条件

设函数 \(z=f(x,y)\) 在点 \((x_0,y_0)\) 的某领域内连续具有一阶及二阶连续偏导数，

又有 \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\)

令 \(f_{xx}(x_0,y_0)=A\;,\;\;f_{xy}(x_0,y_0)=B\;,\;\;f_{yy}(x_0,y_0)=C\)

则 \(f(x,y)\) 在 \((x_0,y_0)\) 处是否取极值的条件如下：

\((1)\;\;AC-B^2>0\;\;\) 时具有极值，且当 \(A<0\) 时有极大值，当 \(A>0\) 时有极小值

\((2)\;\;AC-B^2<0\;\;\) 时没有极值

\((3)\;\;AC-B^2=0\;\;\) 时是否有极值不确定，要具体分析

最值存在定理：在有界闭区域上连续的多元函数在该区域上必有最大的函数值和最小的函数值

条件极值

定义：对自变量作一定限制的极值问题

现有目标函数 \(f(x,y)=0\;\;\) 条件函数：\(\psi (x,y)=0\)

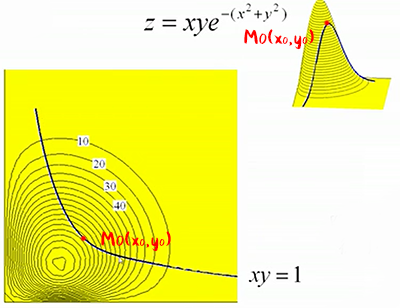
目标函数在 \(M_0(x_0,y_0)\) 取条件极值，则：

\(\triangledown f(x_0,y_0)\) 是等值线 \(z_0=f(x,y)\) 在点 \((x_0,y_0)\) 处的法向量，

\(\triangledown \phi (x_0,y_0)\) 是曲线 \(\phi (x,y)=0\) 在点 \((x_0,y_0)\) 处的法向量，

则曲线 \(\phi (x,y)=0\) 在点 \((x_0,y_0)\) 与函数 \(z=f(x,y)\) 的等值线 \(z_0=f(x,y)\) 相切，

即：\(\triangledown f(x_0,y_0)\parallel \triangledown \phi(x_0,y_0)\)

以下是具体求极值方法：

拉格朗日 \((Largange)\) 乘数法

思路：将目标函数（二元函数）与约束条件结合在一起构造出拉格朗日函数（三元函数），从而将二元函数的条件极值问题转化成三元函数的无条件极值问题

要找函数 \(z=f(x,y)\) 在条件 \(\phi(x,y)=0\) 下可能的极值点，

要先构造函数 \(F(x,y,\lambda )=f(x,y)+\lambda \phi (x,y)\)，其中 \(\lambda\) 为某一常数

各自求偏导后： \(\begin{cases}f_x(x,y)+\lambda \phi_x(x,y)=0\\f_y(x,y)+\lambda \phi_y(x,y)=0\\\phi (x,y)=0\end{cases}\)

分别解出 \(x,y,\lambda\)，其中 \(x,y\) 就是可能的极值点的坐标

代入消元法

适用于约束函数比较简单，且单变量可显示表示的情况，本质是降维打击

将约束条件代入目标函数消元，再解一元函数的极值即可