高等数学A2 2020/4/9 第十四次课

返回主索引

偏导数

定义

一个多元函数关于某一个自变量的变化率

以二元函数关于 \(x\) 的偏导数为例：

$z=f(x,y) $

\(\vartriangle_xz=f(x_0+\vartriangle x,y_0)-f(x_0,y_0)=\lim\limits_{\vartriangle x\to 0}\frac{f(x_0+\vartriangle x)-f(x_0,y_0)}{\vartriangle x}\)

\(\;\;\;\;\;\;\;\;=\frac{\partial z}{\partial x}|_{x=x_0}^{y=y_0}=f_x(x_0,y_0)\)

偏导函数

\(f_x(x,y) \Longrightarrow \frac{\partial z}{\partial x},\;\;\frac{\partial f}{\partial x},\;\;f_y(x,y),\;\;f_x'\)

\(f_y(x,y) \Longrightarrow \frac{\partial z}{\partial y},\;\;\frac{\partial f}{\partial y},\;\;f_x(x,y),\;\;f_y'\)

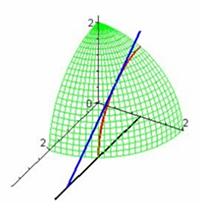
对于多元函数：偏导数存在不能保证函数连续或有极限，函数连续不一定有偏导数（上半圆锥面）

运算规则

把无关自变量暂时视为常量后求导，

亦可先将已知变量值代入简化运算

混合偏导数：偏导了多个自变量的导数，运算规则参考克莱罗定理

克莱罗定理

如果 \(\frac{\partial^2z}{\partial y\partial z}\) 和 \(\frac{\partial^2z}{\partial z\partial y}\) 在区域 \(D\) 内连续，

则在 \(D\) 内：\(\frac{\partial^2z}{\partial y\partial z}=\frac{\partial^2z}{\partial z\partial y}\)

即：在连续的前提下，混合偏导数与对自变量偏导数的先后顺序无关

在不连续处，可能会出现不相等的情况

几何意义

偏导数 \(f_x(x_0,y_0)\) 和 \(f_y(x_0,y_0)\) 分别表示函数 \(f(x,y)\) 在点 \((x_0,y_0)\) 处沿 \(x\) 轴和 \(y\) 轴的变化率

偏导数 \(f_x(x_0,y_0)\) 是曲线 \(l: \begin{cases}z=f(x,y)\\y=y_0\end{cases}\) 在点 \(x=x_0\) 处的切线斜率

即：\(f_x(x_0,y_0)=tan\alpha\)

全微分

二元函数

对于二元函数 \(z=f(x,y)\)：

全增量 \(\vartriangle z=f(x+\vartriangle x,y+\vartriangle y)-f(x,y)\) 且 \(z=f(x,y)\) 在 \((x,y)\) 处可微

若 \(\vartriangle z=A\vartriangle x+B\vartriangle y+O(ρ)\),

则全微分：\(dz\;=\;A\vartriangle x+B\vartriangle y\;=\;A(x,y)\vartriangle x+B(x,y)\vartriangle y\;≈\;\vartriangle z\)

相关定理

\((1)\) 多元函数连续性和是否有偏导数不存在强联系

\((2)\) \(f(x,y)\) 在 \((x,y)\) 处可微，则 \(f(x,y)\) 在 \((x,y)\) 处连续

\((3)\) \(f(x,y)\) 在 \((x,y)\) 处可微，则 \(f(x,y)\) 在 \((x,y)\) 处偏导数都存在

即：\(dz=f_x(x,y)dx+f_y(x,y)dy\)

\((4)\) \(f(x,y)\) 所有偏导数在 \((x,y)\) 处连续，则 \(f(x,y)\) 在 \((x,y)\) 可微