高等数学A2 2020/3/24 第九次课
返回主索引
空间直线及其方程
直线方程的形式
一点和一个非零向量确定
\(∀M(x,y,z),M_0(x_0,y_0,z_0)∈R^3\)
\(M∈L\iff\vec{M_0M}\parallel\vec s\iff\vec{M_0M}=t\vec s\)
点向式方程 \((Vector\;equation)\)：\(\vec r=\vec{r_0}+t\vec s\)
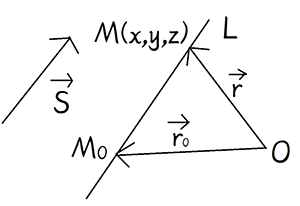
令 \(\vec s=(m,n,p)\Longrightarrow\{x-x_0,y-y_0,z-z_0\}=t\{m,n,p\}\)
参数式方程 \((Parametric\;equation)\)：\(\begin{cases}x=x_0+tm\\y=y_0+tn\;\;\;\;(-\infty <t<+\infty )\\z=z_0+tp\end{cases}\)
其中 \(t\) 为参数
由 \((x-x_0,y-y_0,z-z_0)\parallel (m,n,p)\) 得
对称式方程 \((Symmetrical\;equation)\)：\(\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}\)
直线的标准方程一般指的是点向式方程或对称式方程
两个不平行的平面相交确定
\(\prod_1:A_1x+B_1+C_1z+D_1=0\)
\(\prod_2:A_2x+B_2+C_2z+D_2=0\)
\(\vec{n_1}=(A_1,B_1,C_1)\nparallel\vec{n_2}=(A_2,B_2,C_2)\)
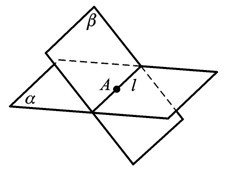
一般式方程\((Basical\;equation)\)：\(L=\begin{cases}A_1x+B_1+C_1z+D_1=0\\A_2x+B_2+C_2z+D_2=0\end{cases}\)
其中 \(L\) 的方向向量 \(\vec s=\vec{n_1}\times\vec{n_2}=(A_1,B_1,C_1)\times(A_2,B_2,C_2)\)
\(L\) 的对称式方程：\(\frac{x-x_0}{B_1C_2-B_2C_1}=\frac{y-y_0}{C_1A_2-C_2A_1}=\frac{z-z_0}{A_1B_2-A_2B_1}\)
进而可推导，
两点式方程\((Twopoints\;equation)\)：\(\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}\)
直线与直线的关系
\(L_1:\frac{x-x_1}{m_1}=\frac{y-y_1}{n_1}=\frac{z-z_1}{p_1}\;\;\;\;\vec{s_1}=(m_1,n_1,p_1)\)
\(L_2:\frac{x-x_2}{m_2}=\frac{y-y_2}{n_2}=\frac{z-z_2}{p_2}\;\;\;\;\vec{s_2}=(m_2,n_2,p_2)\)
\((1)\;L_1\parallel L_2\iff \vec{s_1}\parallel \vec{s_2}\iff \frac{m_1}{m_2}=\frac{n_1}{n_2}=\frac{p_1}{p_2}\)
\((2)\;L_1\parallel L_2\) 且不重合 \(\iff\vec{s_1}\parallel \vec{s_2}\nparallel \vec{M_1M_2}\)
\((3)\;L_1\perp L_2\iff \vec{s_1}\perp \vec{s_2}\iff m_1m_2+n_1n_2+p_1p_2=0\)
\((4)\;L_1,L_2\) 共面 \(\iff[s_1s_2\vec{M_1M_2}]=0\iff\begin{vmatrix}x_2-x_1&y_2-y_1&z_2-z_1\\m_1&n_1&p_1\\m_2&n_2&p_2\end{vmatrix}=0\)
\((5)L_1,L_2\) 异面 \(\iff[s_1s_2\vec{M_1M_2}]\ne0\)
角度和距离的计算
设：两直线的夹角为 \(\gamma\) （锐角）
\(cos\gamma = \frac{|\vec{s_1}\vec{s_2}|}{|\vec{s_1}||\vec{s_2}|}=\frac{|m_1m_2+n_1n_2+p_1p_2|}{\sqrt{m_1^2+n_1^2+p_1^2}·\sqrt{m_2^2+n_2^2+p_2^2}}\)
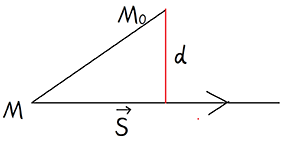
设：点 \(M_0\) 到直线的距离为 \(d\)
\(d=\frac{|Ax_0+By_0+Cz_0|}{\sqrt{A^2+B^2}}\)
直线与平面的关系
\(\prod:Ax+By+Cz+D=0\;\;\;\;\vec n=(A,B,C)\)
\(L:\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}\;\;\;\;\vec s=(m,n,p)\)
\(M_0(x_0,y_0,z_0)\) 为 \(L\) 上一点
\((1)L\parallel\prod\iff\vec s\perp\vec n\iff Am+Bn+Cp=0\)
\((2)L⊆\prod\iff\vec s\perp\vec n\iff Am+Bn+Cp=0\;\;and\;\;M_0∈\prod\)
\((3)L\perp\prod\iff\vec s\parallel\vec n\iff\frac{A}{m}=\frac{B}{b}=\frac{C}{p}\)
\((4)L\) 与 \(\prod\) 相交，夹角为 \(\gamma\)
\(sin\gamma=|cos\theta |=\frac{|\vec n·\vec s|}{|\vec n||\vec s|}=\frac{|Am+Bn+Cp|}{\sqrt{A^2+B^2+C^2}·\sqrt{m^2+n^2+p^2}}\)
平面束
平面束属于一种空间图形，是一组有特殊位置关系的平面的集合，即有一条公共直线的所有平面的集合。平面束指如下的两种平面集合：1.由所有彼此平行的平面组成的集合称为平行平面束；2.由相交于同一条直线的所有平面组成的集合称为共线平面束、有轴平面束或相交平面束，这条直线称为共线平面束的轴。
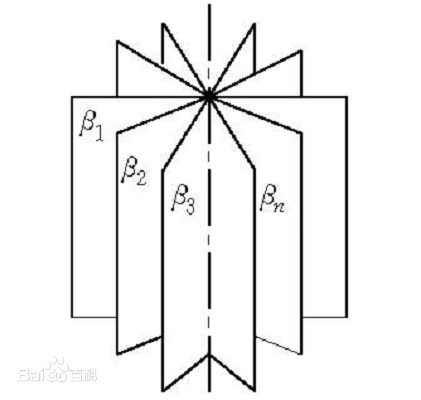
直线 \(L:\begin{cases}x+y-z+1=0\\y+z=0\end{cases}\)
经过直线 \(L\) 的所有平面方程为：\((x+y-z+1)+\lambda (y+z)=0\)
