钟神25五一笔记Day2
树状数组没用。
可持久化
-
能够访问历史版本,且强制在线。
-
常见:数组、并查集、平衡树、线段树。
-
核心:不能修改原来的值。
区间推平一定要先推平,把懒标记删掉。
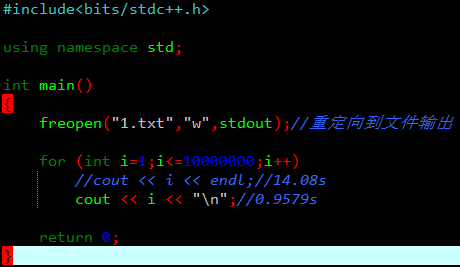
不要写#define int long long,慢4倍。


线段树模板
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define root 1,n,1
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
const int maxn=100010;
int n,m,a[maxn];
struct node//一个线段树节点
{
int sum;//代表区间和
int size;//代表区间长度
int add;//这段区间被整体加了多少
node()
{
sum = size = add = 0;
}
void init(int v)//用一个数初始化
{
sum = v;
size = 1;
}
}z[maxn<<2];//z[i]就代表线段树的第i个节点
node operator+(const node &l,const node &r)
{
node res;
res.sum = l.sum + r.sum;
res.size = l.size + r.size;
return res;
}
void color(int l,int r,int rt,int v)//给l,r,rt这个节点打一个+v的懒标记
{
z[rt].add += v;
z[rt].sum += z[rt].size * v;
}
void push_col(int l,int r,int rt)//标记下放 把标记告诉儿子
{
if (z[rt].add == 0) return; //没标记 不需要下放 可以不要这句话 但会慢些
int m=(l+r)>>1;
color(lson,z[rt].add);
color(rson,z[rt].add);
z[rt].add=0;
}
void build(int l,int r,int rt)//建树 初始化l,r,rt这个节点
//编号为rt的线段树节点 所对应的区间是l~r
{
if (l==r)
{
z[rt].init(a[l]);
return;
}
int m=(l+r) >> 1;
build(lson);
build(rson);
z[rt] = z[rt<<1] + z[rt<<1|1];
}
node query(int l,int r,int rt,int nowl,int nowr)
//l,r,rt描述了一个线段树节点
//nowl nowr代表了询问的区间的左端点和右端点
{
if (nowl <= l && r <= nowr) return z[rt];
push_col(l,r,rt);
int m=(l+r)>>1;
if (nowl<=m)
{
if (m<nowr) return query(lson,nowl,nowr) + query(rson,nowl,nowr);
else return query(lson,nowl,nowr);
}
else return query(rson,nowl,nowr);
}
void modify(int l,int r,int rt,int nowl,int nowr,int v)
//把nowl~nowr这段区间全部整体+v
{
if (nowl<=l && r<=nowr)//当前线段树节点被修改区间整体包含
{
color(l,r,rt,v);//给l,r,rt这个节点打一个+v的懒标记
return;
}
push_col(l,r,rt);
int m=(l+r)>>1;
if (nowl<=m) modify(lson,nowl,nowr,v);
if (m<nowr) modify(rson,nowl,nowr,v);
z[rt] = z[rt<<1] + z[rt<<1|1];
}
int main()
{
cin >> n;
for (int i=1;i<=n;i++)
cin >> a[i];
build(root);
cin >> m;
for (int i=1;i<=m;i++)
{
int opt;
cin >> opt;
if (opt==1)//询问
{
int l,r;
cin >> l >> r;
cout << query(root,l,r).sum << "\n";
}
else
{
int l,r,v;
cin >> l >> r >> v;
modify(root,l,r,v);
}
}
return 0;
}
线段树还要询问 max 和 min 的值模板
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define root 1, n, 1
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
const int maxn = 100010;
int n, m, a[maxn];
struct node // 一个线段树节点
{ // 第一个要修改的地方:要维护的东西
int sum; // 代表区间和
int minv; // 代表区间最小值
int maxv; // 代表区间最大值
int size; // 代表区间长度
int add; // 这段区间被整体加了多少
node()
{
sum = size = add = minv = maxv = 0;
}
void init(int v) // 用一个数初始化
{ // 第二个修改的地方:怎么用一个数初始化
sum = minv = maxv = v;
size = 1;
}
} z[maxn << 2]; // z[i]就代表线段树的第i个节点
node operator+(const node &l, const node &r)
{ // 第三个需要修改的地方:左右儿子怎么合并
node res;
res.sum = l.sum + r.sum;
res.size = l.size + r.size;
res.minv = min(l.minv, r.minv);
res.maxv = max(l.maxv, r.maxv);
return res;
}
void color(int l, int r, int rt, int v) // 给l,r,rt这个节点打一个+v的懒标记
{ // 第四个需要修改的地方:怎么打标记
z[rt].add += v;
z[rt].sum += z[rt].size * v;
z[rt].minv += v;
z[rt].maxv += v;
}
void push_col(int l, int r, int rt) // 标记下放 把标记告诉儿子
{
if (z[rt].add == 0)
return; // 没标记 不需要下放 可以不要这句话 但会慢些
int m = (l + r) >> 1;
color(lson, z[rt].add);
color(rson, z[rt].add);
z[rt].add = 0;
}
void build(int l, int r, int rt) // 建树 初始化l,r,rt这个节点
// 编号为rt的线段树节点 所对应的区间是l~r
{
if (l == r)
{
z[rt].init(a[l]);
return;
}
int m = (l + r) >> 1;
build(lson);
build(rson);
z[rt] = z[rt << 1] + z[rt << 1 | 1];
}
node query(int l, int r, int rt, int nowl, int nowr)
// l,r,rt描述了一个线段树节点
// nowl nowr代表了询问的区间的左端点和右端点
{
if (nowl <= l && r <= nowr)
return z[rt];
push_col(l, r, rt);
int m = (l + r) >> 1;
if (nowl <= m)
{
if (m < nowr)
return query(lson, nowl, nowr) + query(rson, nowl, nowr);
else
return query(lson, nowl, nowr);
}
else
return query(rson, nowl, nowr);
}
void modify(int l, int r, int rt, int nowl, int nowr, int v)
// 把nowl~nowr这段区间全部整体+v
{
if (nowl <= l && r <= nowr) // 当前线段树节点被修改区间整体包含
{
color(l, r, rt, v); // 给l,r,rt这个节点打一个+v的懒标记
return;
}
push_col(l, r, rt);
int m = (l + r) >> 1;
if (nowl <= m)
modify(lson, nowl, nowr, v);
if (m < nowr)
modify(rson, nowl, nowr, v);
z[rt] = z[rt << 1] + z[rt << 1 | 1];
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
build(root);
cin >> m;
for (int i = 1; i <= m; i++)
{
int opt;
cin >> opt;
if (opt == 1) // 询问
{
int l, r;
cin >> l >> r;
cout << query(root, l, r).sum << "\n";
}
else
{
int l, r, v;
cin >> l >> r >> v;
modify(root, l, r, v);
}
}
return 0;
}
可持久化线段树模板
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int cnt;//总共有多少个节点
struct node
{
int l,r;//左儿子 右儿子编号
int sum;//区间和
node(){
l=r=sum=0;
}
}z[maxn*logn];
void update(int p)
{
z[p].sum = z[z[p].l].sum + z[z[p].r].sum;
}
int build(int l,int r)//当前的区间为l~r 是这段区间对应的节点编号
{
cnt++;
int p=cnt;
if (l==r)
{
z[p].sum = a[l];
return p;
}
int m=(l+r)>>1;
z[p].l = build(l,m);
z[p].r = build(m+1,r);
update(p);
return p;
}
int query(int l,int r,int rt,int nowl,int nowr)
//当前线段树节点编号为rt 对应的区间为l~r 要询问nowl~nowr这段区间的和
{
if (nowl <= l && r <= nowr) return z[rt].sum;
int m=(l+r)>>1;
if (nowl<=m)
{
if (m<nowr) return query(l,m,z[rt].l,nowl,nowr) + query(m+1,r,z[rt].r,nowl,nowr);
else return query(l,m,z[rt].l,nowl,nowr);
}
else return query(m+1,r,z[rt].r,nowl,nowr);
}
int modify(int l,int r,int rt,int p,int v)//返回修改后的新节点编号
//当前线段树节点编号为rt 对应的区间为l~r 要把a[p]+=v
{
cnt++;int q = cnt;//新的节点q用于修改
z[q] = z[rt];
if (l==r)
{
z[q].sum += v;
return q;
}
int m=(l+r)>>1;
if (p<=m)//在左儿子
z[q].l = modify(l,m,z[q].l,p,v);
else
z[q].r = modify(m+1,r,z[q].r,p,v);
update(q);
return q;
}
int main()
{
cin >> n;
for (int i=1;i<=n;i++)
cin >> a[i];
cin >> m;
root[0] = build(1,n);//root[i]代表第i次操作后的根节点是谁
for (int i=1;i<=m;i++)
{
int opt;
cin >> opt;
if (opt==1)
{
int p,v;
cin >> p >> v;
root[i] = modify(1,n,root[i-1],p,v);
}
else
{
int k,l,r;
cin >> k >> l >> r;
cout << query(1,n,root[k],l,r) << "\n";
root[i] = root[i-1];
}
}
return 0;
}
主席树(前缀值域可持久化线段树)模板
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int cnt;//总共有多少个节点
struct node
{
int l,r;//左儿子 右儿子编号
int sum;//区间和
node(){
l=r=sum=0;
}
}z[maxn*logn];
void update(int p)
{
z[p].sum = z[z[p].l].sum + z[z[p].r].sum;
}
int query(int l,int r,int rt,int nowl,int nowr)
//当前线段树节点编号为rt 对应的区间为l~r 要询问nowl~nowr这段区间的和
{
if (nowl <= l && r <= nowr) return z[rt].sum;
int m=(l+r)>>1;
if (nowl<=m)
{
if (m<nowr) return query(l,m,z[rt].l,nowl,nowr) + query(m+1,r,z[rt].r,nowl,nowr);
else return query(l,m,z[rt].l,nowl,nowr);
}
else return query(m+1,r,z[rt].r,nowl,nowr);
}
int modify(int l,int r,int rt,int p,int v)//返回修改后的新节点编号
//当前线段树节点编号为rt 对应的区间为l~r 要把a[p]+=v
{
cnt++;int q = cnt;//新的节点q用于修改
z[q] = z[rt];
if (l==r)
{
z[q].sum += v;
return q;
}
int m=(l+r)>>1;
if (p<=m)//在左儿子
z[q].l = modify(l,m,z[q].l,p,v);
else
z[q].r = modify(m+1,r,z[q].r,p,v);
update(q);
return q;
}
int query(int p1,int p2,int l,int r,int k)
//当前对应的值域范围为l~r
//要询问第k小的数
//需要用p1和p2这两颗线段树来询问
{
if (l==r) return l;
int m=(l+r)>>1;
if (z[z[p2].l].sum - z[z[p1].l].sum >= k) return query(z[p1].l,z[p2].l,l,m,k);
//z[z[p2].l].sum - z[z[p1].l].sum代表aL~aR有多少个数在[l,m]之间
else return query(z[p1].r,z[p2].r,m+1,r,k-(z[z[p2].l].sum - z[z[p1].l].sum));
}
int main()
{
cin >> n;
for (int i=1;i<=n;i++)
cin >> a[i];
root[0] = 0;
//root[i] 代表a1~ai这些数所对应的值域线段树的根
//值域范围是1~maxv
for (int i=1;i<=n;i++)
root[i] = modify(1,maxv,root[i-1],a[i],1);
cin >> m;
for (int i=1;i<=m;i++)
{
int l,r,k;
cin >> l >> r >> k;
cout << query(root[l-1],root[r],1,maxv,k) << "\n";
}
return 0;
}
线段树查询区间相邻两数差的绝对值的和模板
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define root 1,n,1
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
const int maxn=100010;
int n,m,a[maxn];
struct node//一个线段树节点
{
int sum;//代表区间相邻两数差的绝对值的和
int lv;//最左边的数是多少
int rv;//最右边的数是多少
int add;//这段区间被整体加了多少
node()
{
sum = add = 0;
}
void init(int v)//用一个数初始化
{
sum = 0;
lv = rv = v;
size = 1;
}
}z[maxn<<2];//z[i]就代表线段树的第i个节点
node operator+(const node &l,const node &r)
{
node res;
res.sum = l.sum + r.sum + abs(l.rv - r.lv);
res.lv = l.lv;
res.rv = r.rv;
return res;
}
void color(int l,int r,int rt,int v)//给l,r,rt这个节点打一个+v的懒标记
{
z[rt].add += v;
z[rt].lv += v;
z[rt].rv += v;
}
void push_col(int l,int r,int rt)//标记下放 把标记告诉儿子
{
if (z[rt].add == 0) return; //没标记 不需要下放 可以不要这句话 但会慢些
int m=(l+r)>>1;
color(lson,z[rt].add);
color(rson,z[rt].add);
z[rt].add=0;
}
void build(int l,int r,int rt)//建树 初始化l,r,rt这个节点
//编号为rt的线段树节点 所对应的区间是l~r
{
if (l==r)
{
z[rt].init(a[l]);
return;
}
int m=(l+r) >> 1;
build(lson);
build(rson);
z[rt] = z[rt<<1] + z[rt<<1|1];
}
node query(int l,int r,int rt,int nowl,int nowr)
//l,r,rt描述了一个线段树节点
//nowl nowr代表了询问的区间的左端点和右端点
{
if (nowl <= l && r <= nowr) return z[rt];
push_col(l,r,rt);
int m=(l+r)>>1;
if (nowl<=m)
{
if (m<nowr) return query(lson,nowl,nowr) + query(rson,nowl,nowr);
else return query(lson,nowl,nowr);
}
else return query(rson,nowl,nowr);
}
void modify(int l,int r,int rt,int nowl,int nowr,int v)
//把nowl~nowr这段区间全部整体+v
{
if (nowl<=l && r<=nowr)//当前线段树节点被修改区间整体包含
{
color(l,r,rt,v);//给l,r,rt这个节点打一个+v的懒标记
return;
}
push_col(l,r,rt);
int m=(l+r)>>1;
if (nowl<=m) modify(lson,nowl,nowr,v);
if (m<nowr) modify(rson,nowl,nowr,v);
z[rt] = z[rt<<1] + z[rt<<1|1];
}
int main()
{
cin >> n;
for (int i=1;i<=n;i++)
cin >> a[i];
build(root);
cin >> m;
for (int i=1;i<=m;i++)
{
int opt;
cin >> opt;
if (opt==1)//询问
{
int l,r;
cin >> l >> r;
cout << query(root,l,r).sum << "\n";
}
else
{
int l,r,v;
cin >> l >> r >> v;
modify(root,l,r,v);
}
}
return 0;
}
线段树区间平方和模板
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define root 1,n,1
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
const int maxn=100010;
int n,m,a[maxn];
struct node//一个线段树节点
{
int sum;//代表区间和
int sum2;//代表区间平方和
int size;//代表区间长度
int add;//这段区间被整体加了多少
node()
{
sum = size = add = 0;
}
void init(int v)//用一个数初始化
{
sum = v;
sum2 = v*v;
size = 1;
}
}z[maxn<<2];//z[i]就代表线段树的第i个节点
node operator+(const node &l,const node &r)
{
node res;
res.sum2 = l.sum2 + r.sum2;
res.sum = l.sum + r.sum;
res.size = l.size + r.size;
return res;
}
void color(int l,int r,int rt,int v)//给l,r,rt这个节点打一个+v的懒标记
{
z[rt].add += v;
z[rt].sum2 = z[rt].sum2 + 2*v*z[rt].sum + z[rt].size * v * v;
z[rt].sum += z[rt].size * v;
}
void push_col(int l,int r,int rt)//标记下放 把标记告诉儿子
{
if (z[rt].add == 0) return; //没标记 不需要下放 可以不要这句话 但会慢些
int m=(l+r)>>1;
color(lson,z[rt].add);
color(rson,z[rt].add);
z[rt].add=0;
}
void build(int l,int r,int rt)//建树 初始化l,r,rt这个节点
//编号为rt的线段树节点 所对应的区间是l~r
{
if (l==r)
{
z[rt].init(a[l]);
return;
}
int m=(l+r) >> 1;
build(lson);
build(rson);
z[rt] = z[rt<<1] + z[rt<<1|1];
}
node query(int l,int r,int rt,int nowl,int nowr)
//l,r,rt描述了一个线段树节点
//nowl nowr代表了询问的区间的左端点和右端点
{
if (nowl <= l && r <= nowr) return z[rt];
push_col(l,r,rt);
int m=(l+r)>>1;
if (nowl<=m)
{
if (m<nowr) return query(lson,nowl,nowr) + query(rson,nowl,nowr);
else return query(lson,nowl,nowr);
}
else return query(rson,nowl,nowr);
}
void modify(int l,int r,int rt,int nowl,int nowr,int v)
//把nowl~nowr这段区间全部整体+v
{
if (nowl<=l && r<=nowr)//当前线段树节点被修改区间整体包含
{
color(l,r,rt,v);//给l,r,rt这个节点打一个+v的懒标记
return;
}
push_col(l,r,rt);
int m=(l+r)>>1;
if (nowl<=m) modify(lson,nowl,nowr,v);
if (m<nowr) modify(rson,nowl,nowr,v);
z[rt] = z[rt<<1] + z[rt<<1|1];
}
int main()
{
cin >> n;
for (int i=1;i<=n;i++)
cin >> a[i];
build(root);
cin >> m;
for (int i=1;i<=m;i++)
{
int opt;
cin >> opt;
if (opt==1)//询问
{
int l,r;
cin >> l >> r;
cout << query(root,l,r).sum << "\n";
}
else
{
int l,r,v;
cin >> l >> r >> v;
modify(root,l,r,v);
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号