线段树(区间树)
线段树(Interval Tree),也叫区间树。它在各个节点保存一个区间(即“子数组”),适用于和区间统计有关的问题。比如某些数据可以按区间进行划分,按区间动态进行修改,而且还需要按区间多次进行查询,那么使用线段树可以达到较快查询速度。实际可应用于例如RMQ,线段求长,矩形交,矩形并等,它基本能保证每个操作的复杂度为O(log n)。
一、基本结构
对于一个[0 , N-1]的序列,它对应的线段树的根节点表示区间[0 , N-1],即所有N个数所组成的一个区间,然后,把区间分成两半,分别由左右子树表示。它的左右子树可以有多种表示方法:
方案一:左结点代表的区间为[a , (a + b) / 2],右结点代表的区间为[ (a + b) / 2 + 1 , b ]。叶子节点为区间[a , a]。
其中(a + b) / 2将向下取整,这是最常用的表示方法,当只考虑区间内的整数点时,在这种表示方案情况下的问题求解比较清晰。
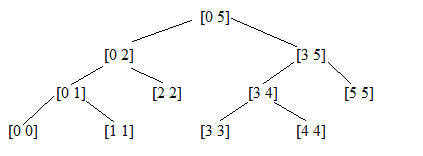
叶子节点数目为N,即整个线段区间的长度,而线段树的总结点数可用数学归纳法证明为2N-1。
方案二: 对于根节点为[0 , N)的区间。
左结点代表的区间为[a , (a + b) / 2),右结点代表的区间为[ (a + b) / 2 , b ]。叶子节点为区间[a , a+1)。
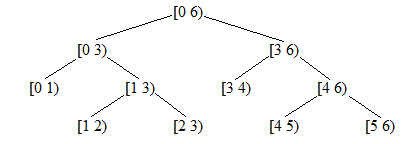
这种方案能覆盖区间内的所有实数点。
不管采用哪种方案,线段树都是平衡二叉树。线段树的总结点数为O(2N),高度为O(log n)。
二、基本操作
建树,插入,删除,查询,更新。
因为它是一棵二叉树,所以它的操作一般除了建树是O(N),其余的都是O(log n)的。
线段树的一般解题过程是先建树,然后插入数据,然后更新,查询。建树和插入删除操作都可由定义直接递归得到。我们来看看线段树的查询和更新操作,特别是在某个区间内进行时的实现方法。
2.1 查询
2.1.1 单点查询
2.1.2 区间查询
区间查询指用户输入一个区间,获取该区间的有关信息,如区间中最大值,最小值,第N大的值等。比如在前面一个图中所示的树中查询最小值,如果询问区间是线段树的一个完整节点,比如是[0,2]或者是[3,3],则可以直接找到对应的节点。但比如[0,3],是由两个区间组合而成。需要把[0,2]和[3,3]两个区间(它们在整数意义上是相连的两个区间)的最小值“合并”起来,也就是求这两个最小值的最小值,才能求出[0,3]范围的最小值。同理,对于其他询问的区间,也都可以找到若干个相连的区间,合并后可以得到询问的区间。
// node 为线段树的结点类型,其中Left 和Right 分别表示区间左右端点
// Lch 和Rch 分别表示指向左右孩子的指针
void Query(node *p, int a, int b) // 当前考察结点为p,查询区间为(a,b]
{
if (a <= p->Left && p->Right <= b)
// 如果当前结点的区间包含在查询区间内
{
...... // 更新结果
return;
}
Push_Down(p); // 将A的标记p移到子结点中,需要更新子结点的值和标记
int mid = (p->Left + p->Right) / 2; // 计算左右子结点的分隔点
if (a < mid) Query(p->Lch, a, b); // 和左孩子有交集,考察左子结点
if (b > mid) Query(p->Rch, a, b); // 和右孩子有交集,考察右子结点
}这样的过程一定选出了尽量少的区间,它们相连后正好涵盖了整个[l,r],没有重复也没有遗漏。同时,这样的区间集合在每层的节点最多会被选取2个,一共选取的节点数也是O(log n)的,因此查询的时间复杂度也是O(log n)。
线段树并不适合所有区间查询情况,它的使用条件是“相邻的区间的信息可以被合并成两个区间的并区间的信息”。即问题是可以被分解解决的。
2.2 更新
2.2.1 单个点的更新
对于单个节点,从根开始按子树的划分确定是访问哪个子树,递归下去,修改叶节点信息,然后回溯修改父节点的信息。
2.2.2 区间更新
当用户更新一个区间的值时,如果连同其子孙全部更新,则改动的节点数为O(n)个。因而,如果要想把区间更新操作也控制在O(log
n)的时间内,只更新O(log n)个节点的信息就成为必要。
借鉴前一节区间查询用到的思路:区间更新时如果区间,完全包含了区间A,则只更新A并回溯更新A的所有祖先节点,但不去更新它的儿子节点。为了记录A的儿子节点的信息事实上已经被改变了,这就需要我们在A节点里增设一个域:标记。
标记记录这个结点是否已被进行了某种更新操作(这种更新操作会影响其所有子结点,但不会影响A本身)。还是像上面的一样,对于任意区间A,如果A完全包含于需要更新的区间,则给A结点标上标记p并更新A的值,然后回溯到祖先节点,但并不给A的祖先节点标标记p,也不给子节点标标记p。在更新和查询的时候,如果我们到了一个结点B,并且当我们决定考虑其子结点,那么就要看看结点B有没有标记p,如果有,就要先按照标记p更新其子结点的值,并且给子结点都标上相同的标记p,同时消掉B的标记p。
// node 为线段树的结点类型,其中Left 和Right 分别表示区间左右端点
// Lch 和Rch 分别表示指向左右孩子的指针
void Update(node *A, int a, int b) // 当前考察结点为A,更新区间为[a,b]
{
if (a <= A->Left && A->Right <= b)
// 如果当前结点的区间包含在更新区间内
{
...... // 修改当前结点的信息
...//标上标记p
return;//从此处开始回溯到祖先节点
}
Push_Down(p); // 将A的标记p移到子结点中,需要更新子结点的值和标记
int mid = (A->Left + A->Right) / 2; // 计算左右子结点的分隔点
if (a < mid) Update(A->Lch, a, b); // 和左孩子有交集,考察左子结点
if (b > mid) Update(A->Rch, a, b); // 和右孩子有交集,考察右子结点
Update(A); // 递归后回溯修改A的信息(因为其子结点的信息可能有更改)
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号