微分方程

微分方程解的性质与结构

一阶

一阶微分方程只能有一个任意常数C，二阶微分方程才能有两个任意常数C
齐次特解线性组合任然是齐次解
\(y1-y2\) 一定非零，A、B都有可能为0

tag:wa1
√

二阶

结论也也行


判断两其次解是否线性相关：两者相除看是否为常数

也可以暴力算，一阶二阶导数全部求出来，把a、b、c全搞出来
tag:hard
√

重点题

• 硬算不丢人
• 也可以令 y = C（常数），可知y=C为其次一特解，\(\frac{x^{-3}}{C}\) 不为常数，两者线性无关
  tag:wa1
  √
  
  利用线性无关判别
  tag:wa1\hard
  ×
  
  结论
  或者和题解一样
  
  叠加定理
  
  系数为1为非齐次特解
  tag:hard
  √
  

高阶齐次

tag:wa1/hard
三角函数有一个特解占两个根 0+i/0-i
√


tag:wa1/hard

一阶计算

基本类型

x、y线性组合（加减）换元

\(\frac{y}{x}\) 换元

套公式

非齐次项为分段函数（系数含绝对值包含在内）

隐含了条件，注意能不带绝对值就不带绝对值（因此多用公式，而不是分离参数法）

伯努利方程（了解）

非齐次项本来是 q(x)，现在含 y，把含 y 项除过去凑微分

口口y'

凑微分思想

• 凑
• 把口除过去

2yy'

xy'

1. 转化为\(\frac{y}{x}\)
   

三角y'

其他y'

这两题都可以当作伯努利做
伯努利：非齐次项本来是 q(x)，现在含 y，把含 y 项除过去凑微分

口口dx口口dy与其他类型

简单分离

齐次

以下三个方法搞懂就够用了
方法：

1. 齐次
2. 判断是否为全微分方程
   1. 偏积分
   2. 凑微分，核心式子 \(d(uv)=udv+vdu\)
      
      
      
      
      
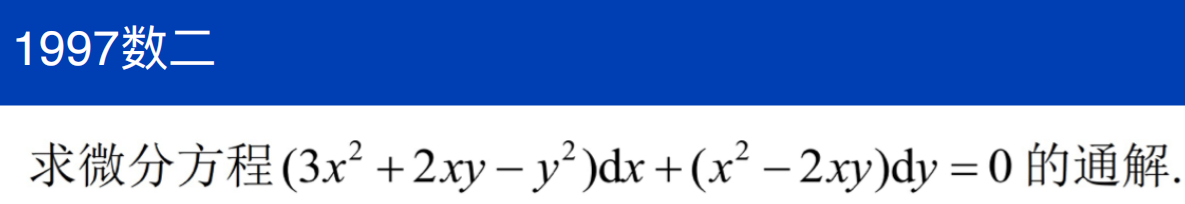
      这题仅做凑微分训练
      注意：要先验证是全微分方程才能凑微分，答案省略了验证过程
      
      y'形式和\(\frac{dy}{dx}\) 等价
      tag
      

非齐次/无法判断是否齐次（一阶线性）

方法：

1. 转换为y'，套公式
2. 判断是否为全微分方程
   1. 偏积分
   2. 凑微分，核心式子 \(d(uv)=udv+vdu\)
      
      
      
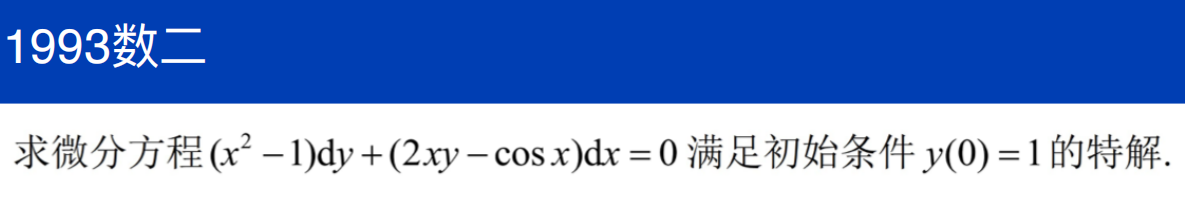
      省略了验证全微分
      
      
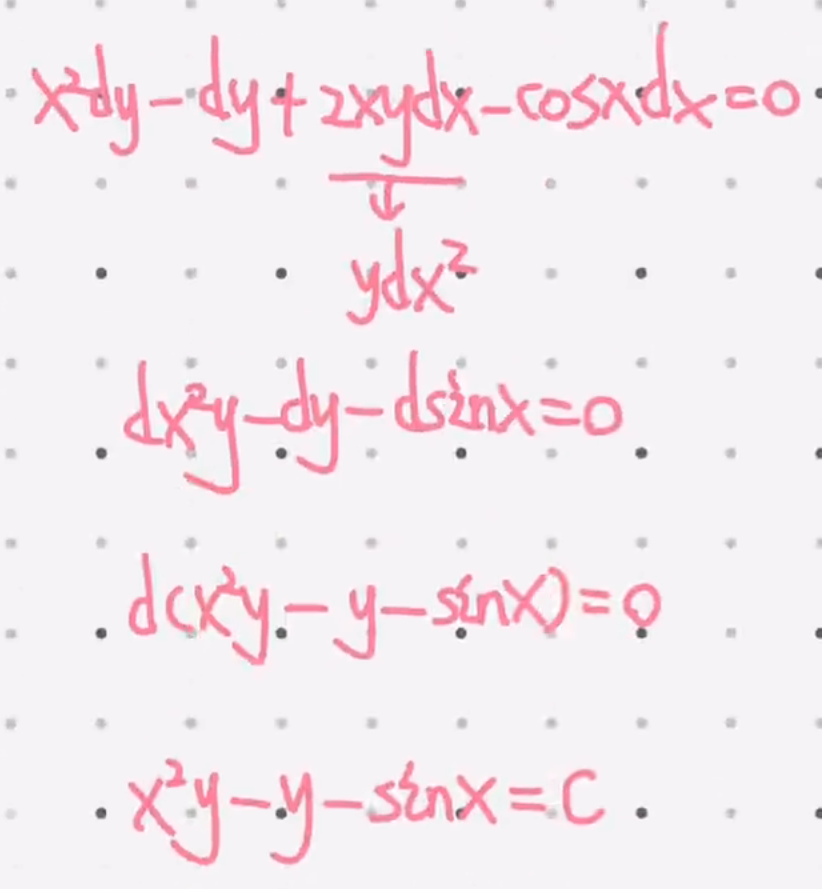
      三种方法，但是只训练凑微分
      省略验证全微分
      

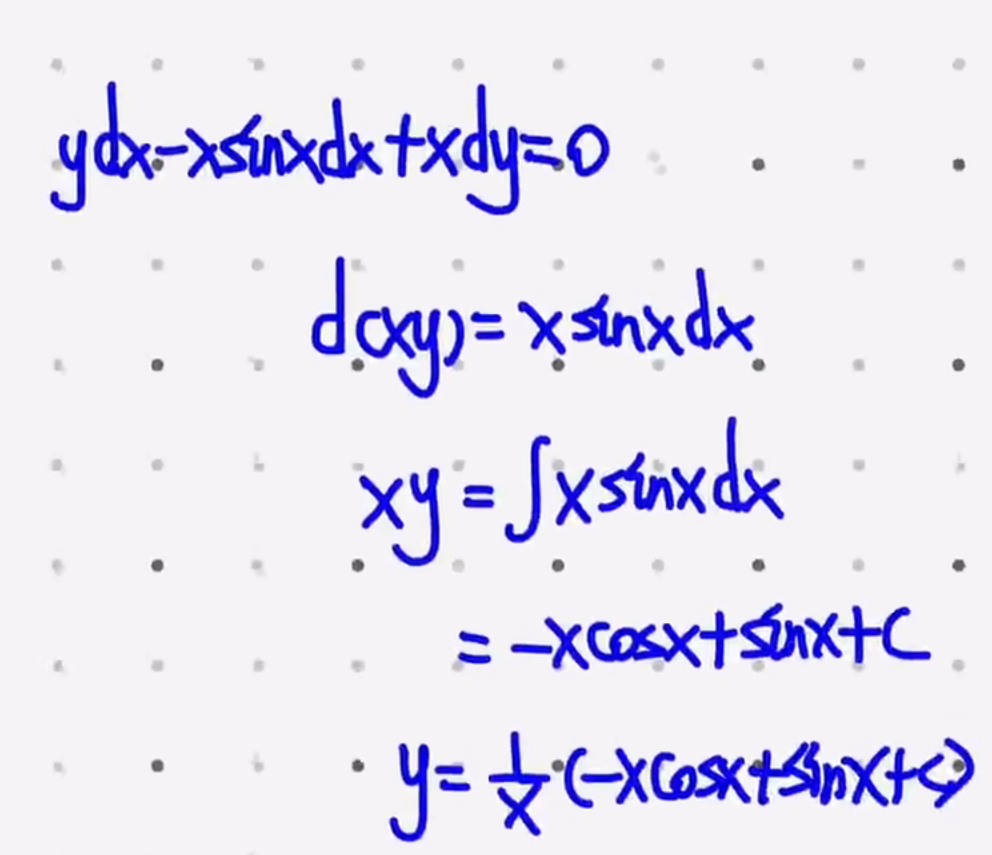
含根号下的平方和

• 利用平方差化简
• 两式子消元
• 特别注意 x 化入根号的正负号问题
  
  

交换 x、 y 地位！！！

1. **y的次方高，\(\frac{dx}{dy}\)
2. 比不出谁次方高，都试试
3. 全微分

y的次方高，\(\frac{dx}{dy}\)
易错，解出来有两个符合条件的，要按照题目要求进行选择

比不出谁次方高，都试试





tag

含多个三角

含\(y^x\)

复杂的想凑微分

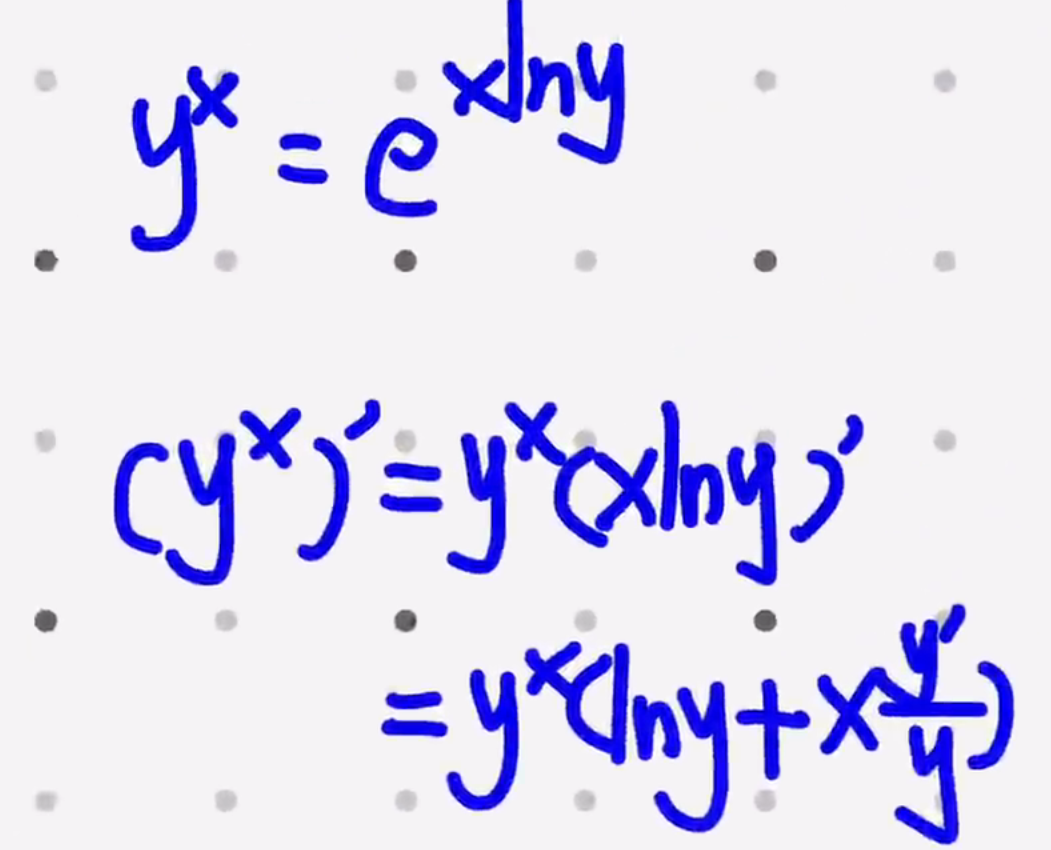
二阶计算

二阶常系数线性齐次

二阶常系数线性非齐次

只设不求

非齐次项为幂指函数

非齐次项为三角函数

非齐次项含有未知数

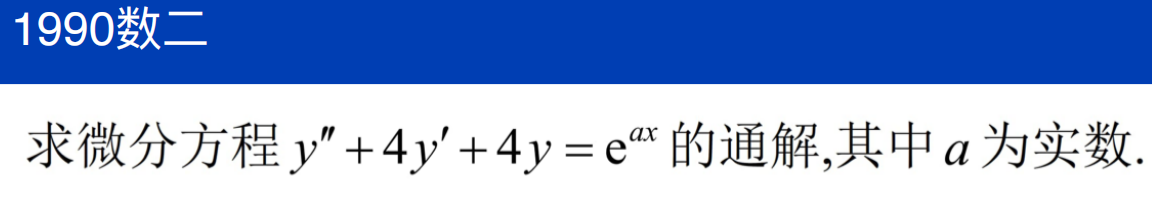
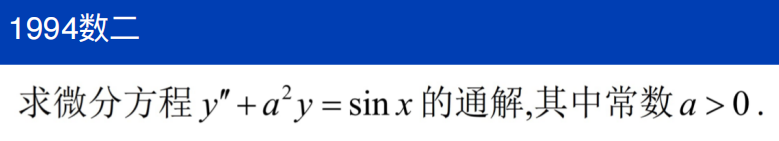
非齐次项为分段函数

齐次项未知

含未知式子的直接代入同类型
^9956f1

二阶变系数

二阶可降阶

不显含y

p次方高，除dp除p

不显含x

欧拉方程

学有余力再看补充 2:44:50
https://www.bilibili.com/video/BV1CpM8ztEaX?t=9889.8
下述结论只能小题用


用上面的结论做

反函数

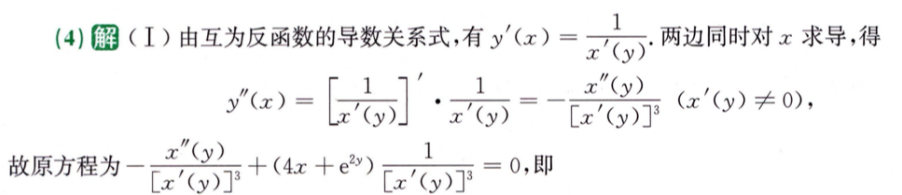
三角换元（欧拉）

引入 t 消掉 x

引入t消去x

其他

引入u消掉y

含有未知式子的直接代入同类型]
^6a03af

套欧拉方程结论

高阶常系数线性齐次方程

齐次

非齐次

• 齐次按高阶来
• 非齐次项特解按照二阶来就行
  
  
  
  

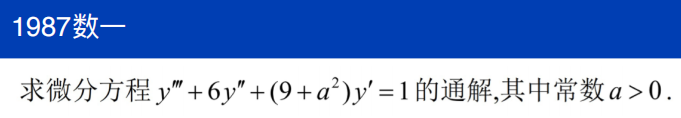
已知解反求微分方程

一阶

1. 给特解代入方程
   • 运用结论推导齐次、非齐次解代入
2. 由方程直接求导
   • 消C这样的变量
     运用结论推导齐次、非齐次解代入
     
     设出方程结构
     ^51c8ff

想办法消掉变化的元素

二阶

1. 由通解求导
2. 由解的性质反推
3. 代入
   
   
   由方程直接求导得到类似题目
   y'那里把C放一边其他的放在另外一边求导，消掉C
   
   综合的一题
   
   
   
   
   
   

三阶以以上

处理微分方程的解

微分方程解的有界性、奇偶性、周期性

大题考积分结合周期性的证明

转不定积分为变限积分

显然只有解的结构为三角函数时，才可能在所有位置有界，若带\(e^x\) 必定有一端无穷大，选C



？？？

微分方程解的极限及渐近线

微分方程解的反常积分（结论）

一个重要结论
\(\Large 微分方程y''+Ay'+By=0,任一解 y(x) ，反常积分 \int_{0}^{+\infty} y(x) \, dx 均收敛，A、B均为常数\)

• \(\Large A>0,B>0\)
  \(\Large 微分方程y''+Ay'+By=0,任一解 y(x) ，反常积分 \int_{-\infty}^{0} y(x) \, dx 均收敛，A、B均为常数\)
• \(\Large A<0,B>0\)

这类题最后求反常积分时，一般都是f(x)用原来微分方程的y'、y''表示




利用结论

有几个没搬进来的，待补

以各种形式给出的微分方程

极限形式

\(\Large 1^{\infty}=u^v=e^{v*(u-1)}\)

含导数等式

导数定义

值得注意的一点：y可导，因此y连续，又y(0) > 0，y！=0，因此y是一个恒大于0的，因为若有负数，连续函数必定有0点
对于这题导数定义需要记一下



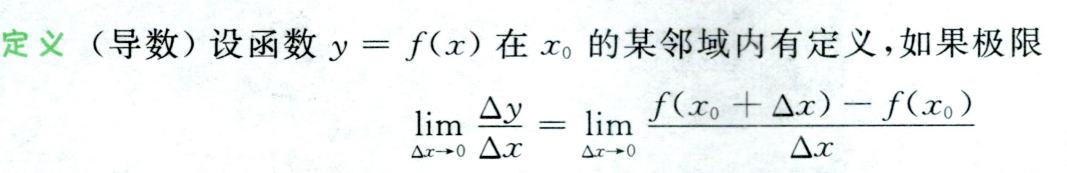
值得注意的一点：y可导，因此y连续，又y(0) > 0，y！=0，因此y是一个恒大于0的，因为若有负数，连续函数必定有0点

牛逼题目
\(\Large 由连续性可以推导lim \Delta y=0\)

导数应用（切法线、曲率）

1. 嗯算
2. 等分点化简
3. \(\large \frac{y}{x}看作(x,y)到(0,0)的斜率\)
4. 法线 * 切线 = -1
5. 注意算面积这种东西一定要加绝对值
   
   奇怪的处理手法，可以多看看怎么操作的
   
   有余力，再做
   
   好题
   
   
   
   
   好题，利用等分点简化计算
   
   好题
   
   
   
   
   
   
   
   
   
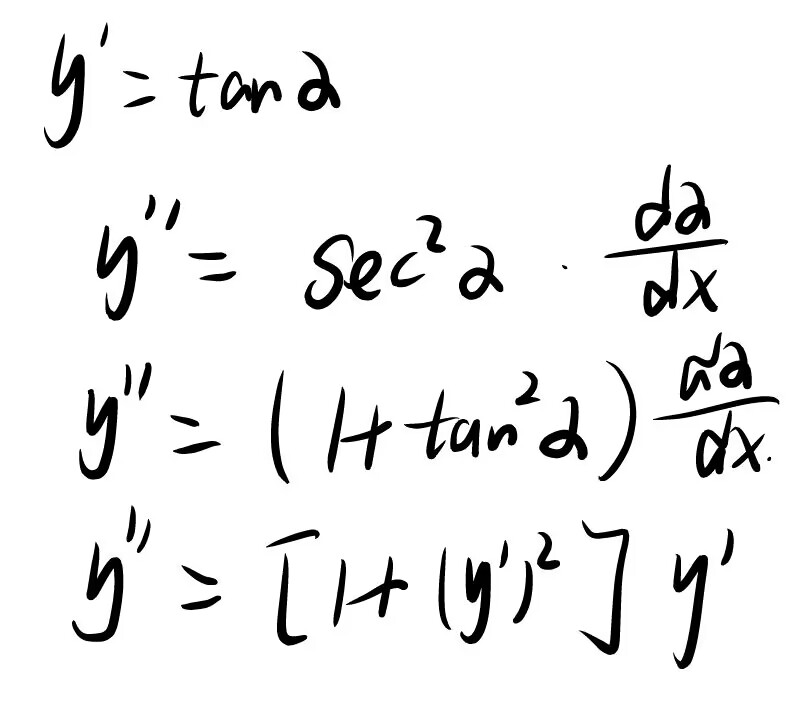
   套公式题
   
   
   套公式题
   

变限积分（待补充）

定积分应用（待补充）

好题
思考方向：列出式子求导后，求了好几次发现变成了变系数的微分方程，我们做的所有都是建立在常系数的前提下，因此要换元

多元微分

1. 把括号里面的东西设为 u，简化式子，这样做的好处在于：u对x、y求偏导得到的式子是相同的
   
   
   
   
   tag
   好题
   

二重积分

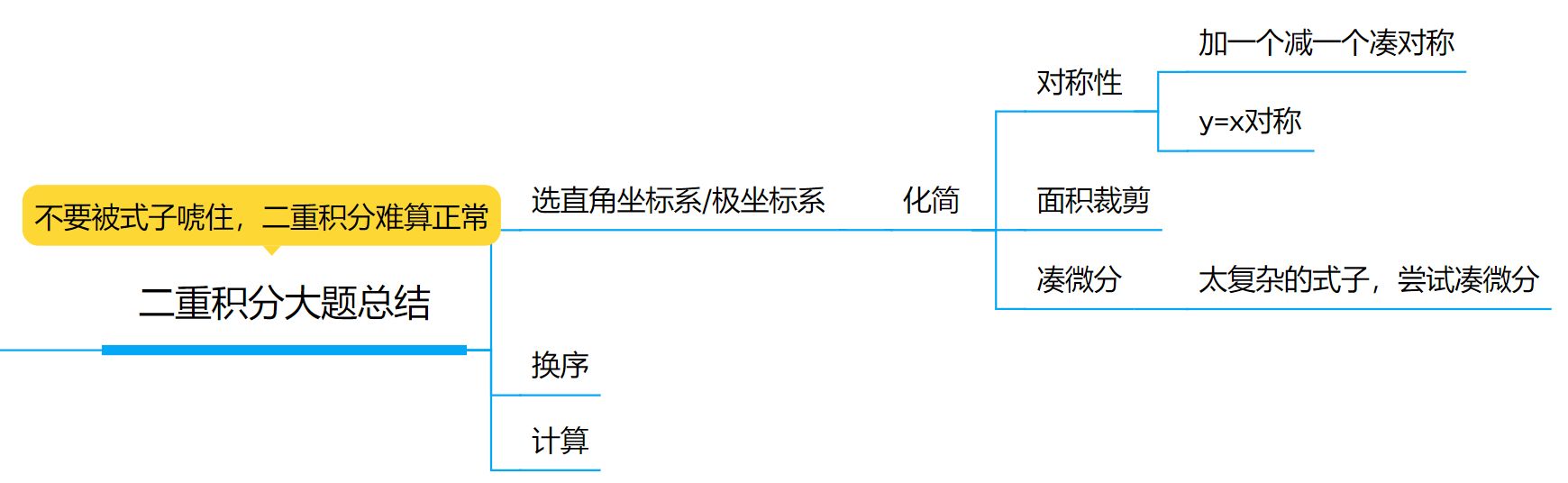
1. 注意标出x的范围
   
   tag
   注意这里变限积分上限有x，被积函数有x，必须换元
   
   tag
   难度在化简二重积分
   
   
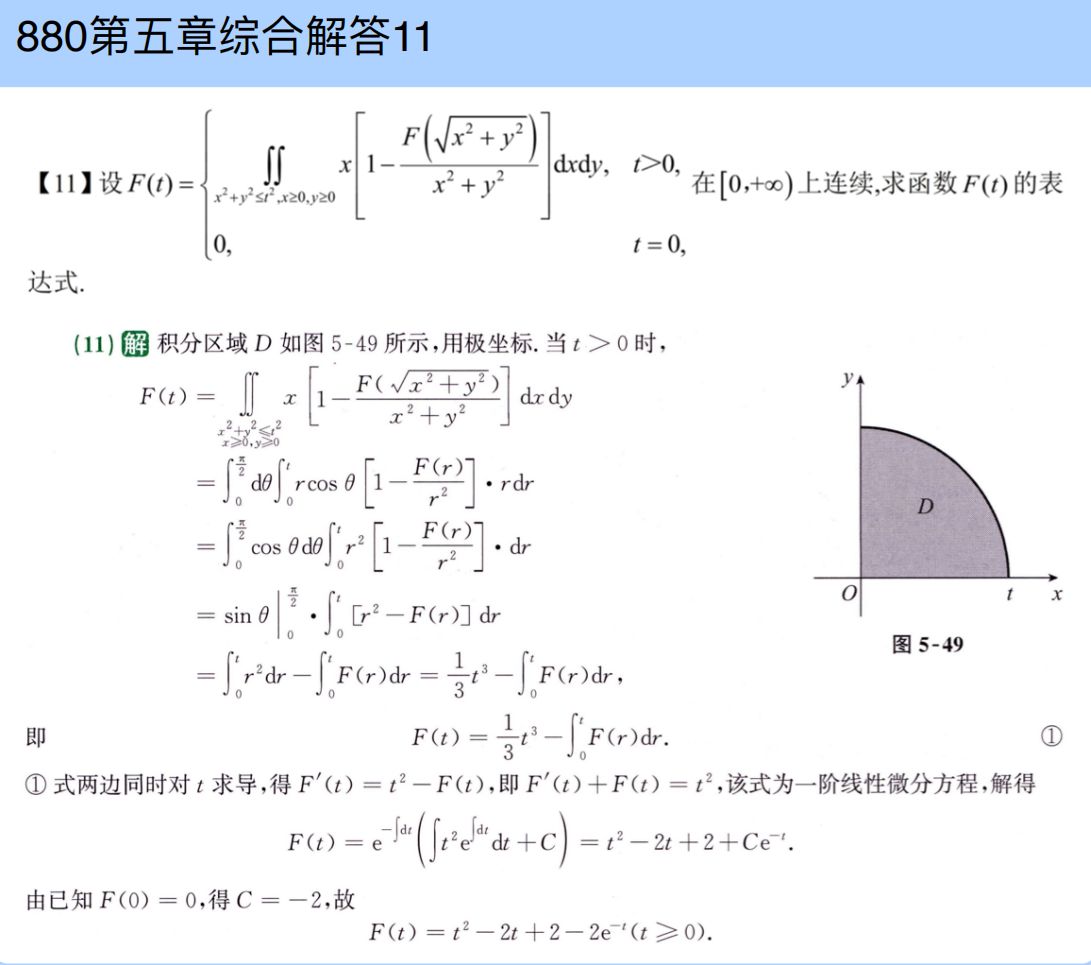
   动手做做
   tag
   

物理应用（待补充）

抓住走过的路程就是弧长