线性代数

tag: 0 - 做错、1 - 做对、2 - 做对但多看
flag:大题，其他和tag一致

行列式

三对⻆线⾏列式

么字型

---

范蒙德

---

行和/列和相等*

余子式（代数）求和

当成两个变量

元素和一致

tag:hard

对角余子式之和

所有余子式之和

总体复盘：很多个元素的所有代数余子式之和只能正常做，但是如果不太多的话，可以考虑分组做
\(A^*=|A|A^{-1}\)

tag:wa

杂项

确定f(x) 中x某次方的系数

定义做，可以先考虑化简

tag:wa1

f(x)=0根的个数

tag:wa1

抽象行列式计算

胖矩阵

胖的是行列式为0

---

构造矩阵

构造要相呼应


(A+B)^{-1} 不能直接求 (AB)^{-1} 才能求

结合特征值！！！

！！！实对称 + 特征值

• 实对称矩阵特征值全为实数，故舍弃共轭复根
• 实对称矩阵必可相似对角化
• 相似对角化的矩阵，r(A) = 非零特征值个数
  
  
  

正交矩阵+转置妙用

结合相似

构造矩阵

好题！！！

结合展开定理！！！

基于性质构造两式相加求行列式

暴力

矩阵

逆

具体矩阵求逆

• 分块矩阵
• 嗯求
  练手
  
  

抽象矩阵求逆 (5)

tag2,1

tag2,1


tag2,

tag2,0


长除就行
tag2,1

（不）可逆的判定与证明

结合特征值（值得全看）

上题备注：这种A多项式形式可以直接求特征值

上题备注：这种A多项式形式可以直接求特征值

结合行列式（2）

非奇异：可逆

tag2,2
证明他就从他入手

和上题结合看

第二问可以放了
tag2，2

练手

tag2，2

tag2，1

可以从可逆矩阵行列式不为0考虑，|A| !=0 ，|B| * |C| = |A|，|B| != 0 |C| !=0

tag2，2
这种列向量证明可逆，一般都可以从秩为1的特征值考虑file-20250731110729744

伴随矩阵

伴随性质

1. \(\Large AA^*=0\) 有着很丰富的性质，要多关注
   tag2，0
   好题！！！

• 第一个
• 第三个，\(A^*\) 特征值是出了本身特征值以外的其他特征值乘积
• 第四个，知一求二，还有一个角度：相同的特征向量
  
  tag2，2
  好题，也可以嗯算
  

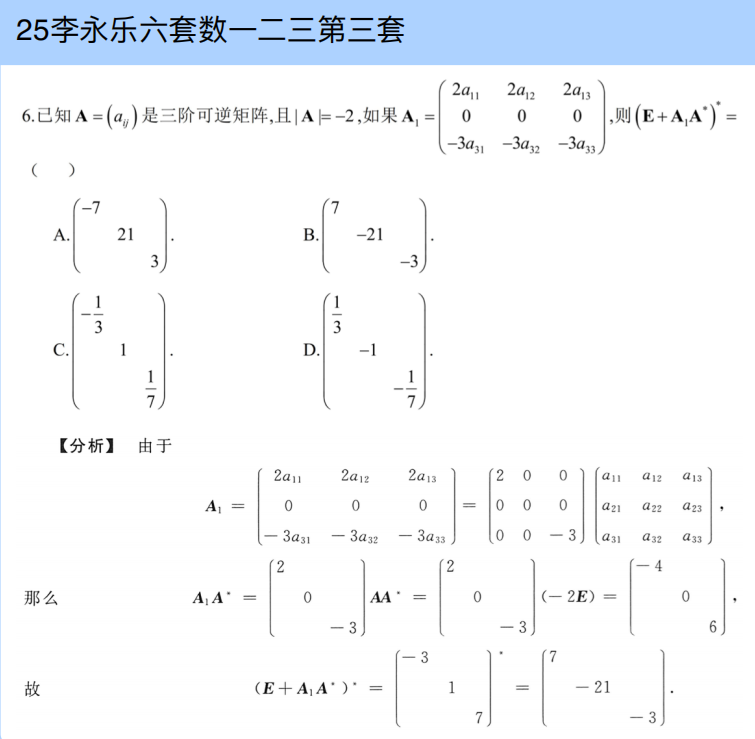
伴随=转置（倍数）

通常使用展开定理排除不合法的解
tag2，1
好题

tag2，1

tag2，2
好题！！！
给出行列式为0，不止可能是想让你配凑，还可能是让你往特征值上想（感觉特征值、秩更有用）

tag2
好题！！！
A 和 \(A^*\) 同时出现，想秩
举例E

秩

求秩及证明秩

1. 秩的性质
2. 分块矩阵
3. 线性无关
   
   tag2
   
   tag2
   好题
   方法二也可以看看，多个思考角度
   
   tag2
   
4. 线性无关
5. 分块矩阵
   
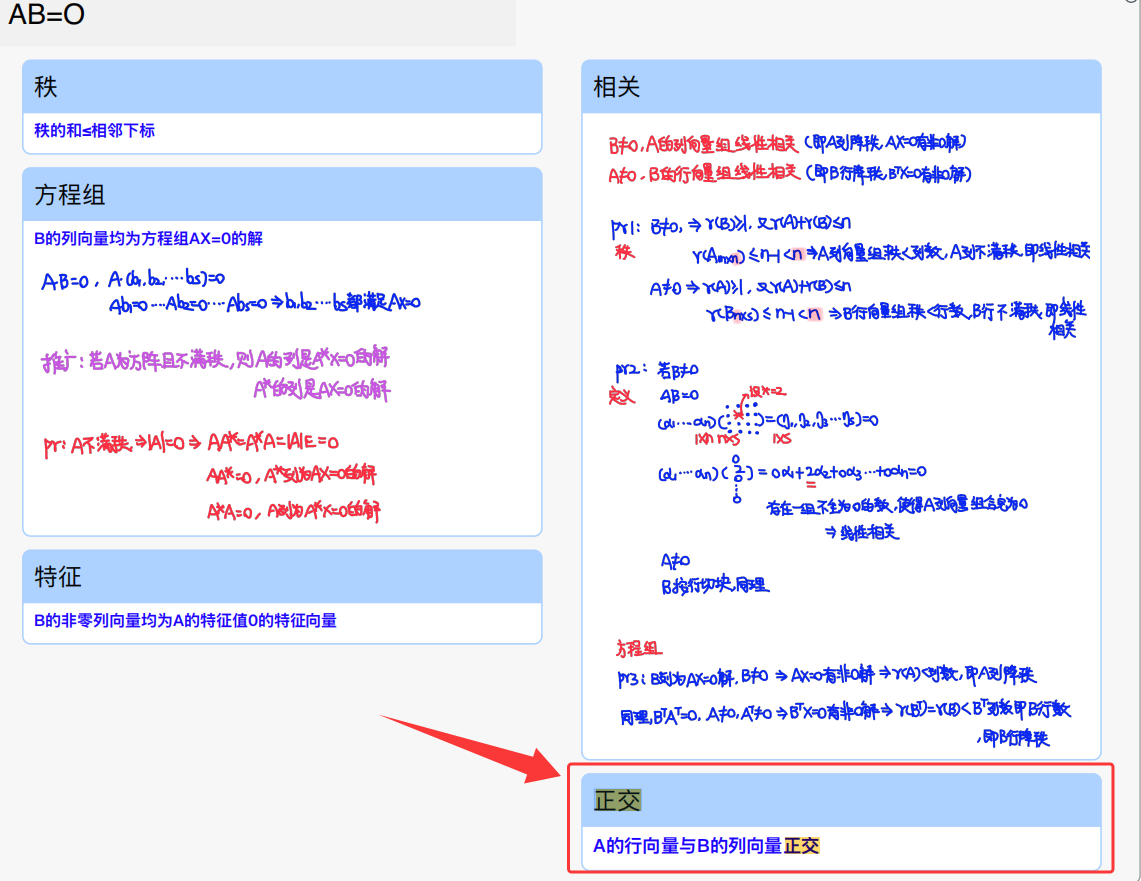
   重要性质：\(AA^{T}\) 一定是实对称的 \((AA^{T})^{T} = AA^{T}\)
   tag2
   

• B 特征值为 1（tr(B)）、0、0，
  • 可得到 \(E - AA^{T}\) 特征值为 0、1、1，同时这个矩阵也是实对称(秩=非零特征值个数，建立在实对称基础之上)
  • 故秩为2
• \(A = E - aa^{T}\)求个\(A^2\) 发现 \(A^{2}=A\) ，\(r(A) + r(A-E) = 3，A-E=-aa^{T},r(A-E)=1\)
  • 故秩为2
    
    tag2
    
    
    tag2
    
    tag2
    可以用r(A-E)+r(A-2E)>=r((A_E)-(A-2E))
    
    tag2，0
    待特值吧，用E=A=B
    

结合相似

1. A可相似对角化，则B为关于A的多项式也可以相似对角化,有一样的特征向量
2. A、B相似 f(A)~f(B)
   tag2,0
   重要！！！
   
   特征值为 -1 的只提供了一个特征向量 r = 2
   特征值为 2 的提供了一个特征向量 r = 2
   又 A-E 特征值为 1 不是这个矩阵的特征值，那么 |A - E| != 0，满秩 r = 3
   
   tag2，2
   
   
   B 不能相似对角化，因此不能直接由特征值非零个数得到秩
   tag2，2
   结论：\(\Large A \sim \Uplambda \rightarrow f(A) \sim f(\Uplambda)\)
   

也可以从分块矩阵的秩来看
tag2，2

利用秩推理

tag2,0

tag2,0

tag2,0

已知秩求参数

挑三阶子式
tag2，2

tag2，2

tag2，2

高次幂

相似

大题中求高次幂一定是用相似对角化那套
flag2，2

flag2,0
1


乘法优化和三阶求逆（A*）




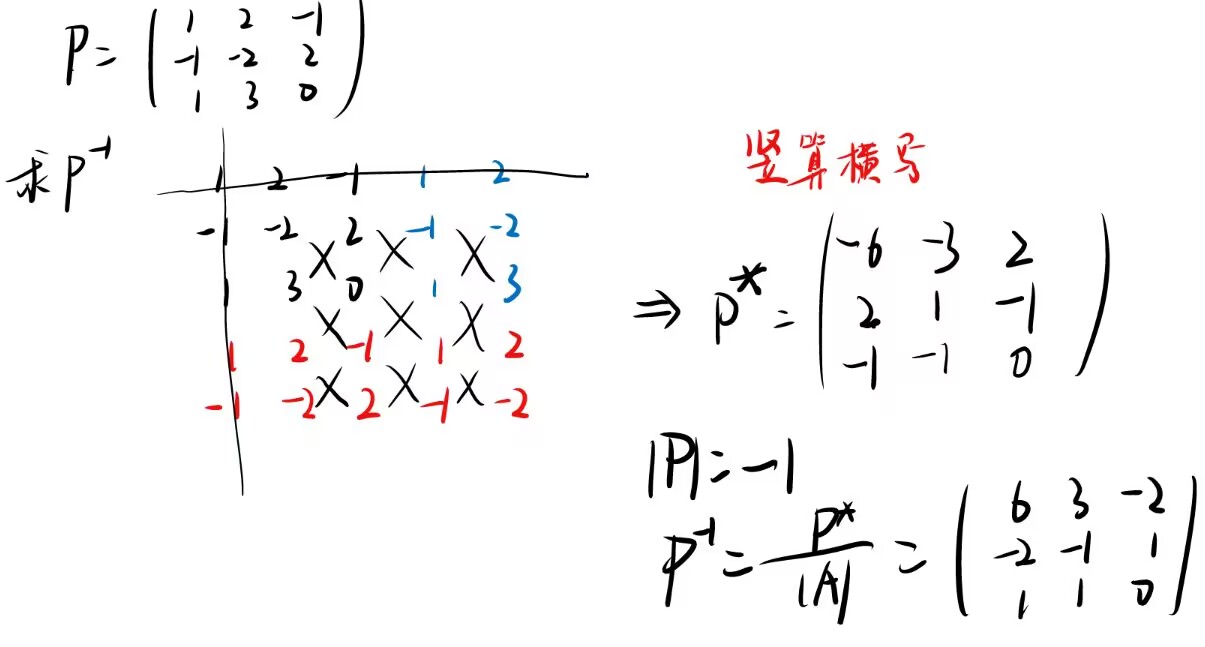
flag2,0
1



flag2,0
0
BA=0往方程组上想


BA = 0,说明B行向量和A列向量正交
使用知二求一


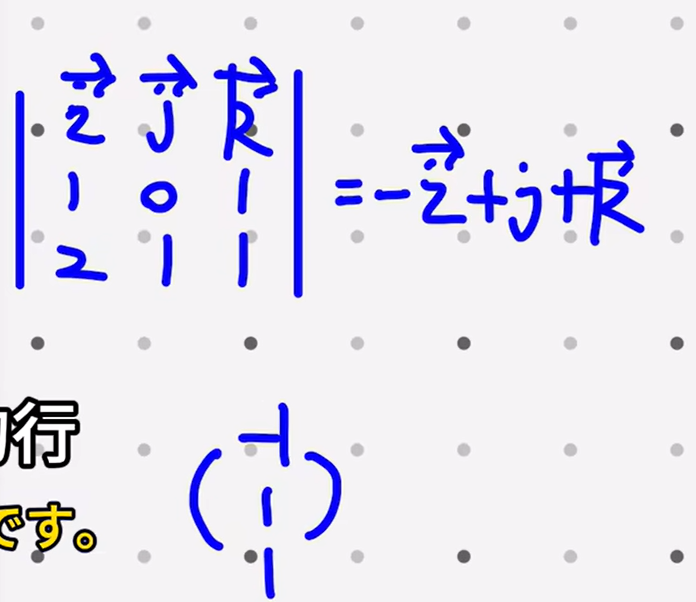
tag2,0
不要忘记前面的系数

flag2，2



齐次方程组2个基础解系 n - r(A) = 2
A 秩为 1

知二求一
知道两个齐次方程组解（列），求秩为1的A的行


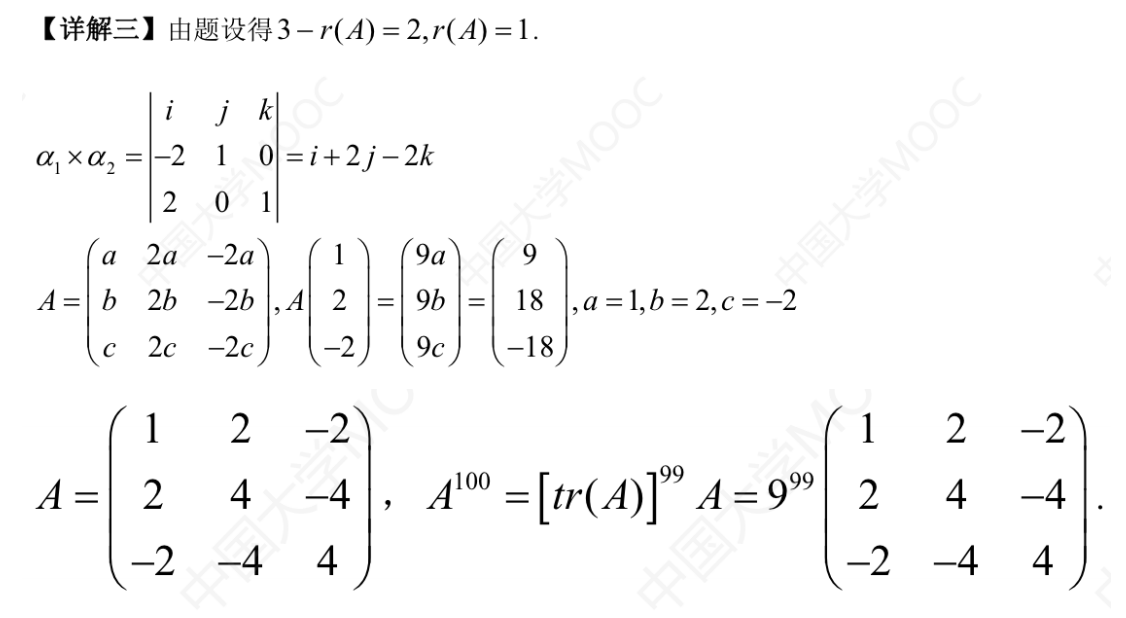
tag2，0

tag2，0

flag2，0
1

分解

tag2，2

初等变换与初等矩阵

tag2，2

tag2,0
跳过先

tag2，2

1. 嗯代入
   
   tag2，0
   
   
   
   flag2，2
   
   flag2，0
   

分块矩阵

分块矩阵的逆和伴随

\(A实对称,A^{*}也实对称\)


tag2,0

tag2,0


tag2,2

E万能，用E消去别的

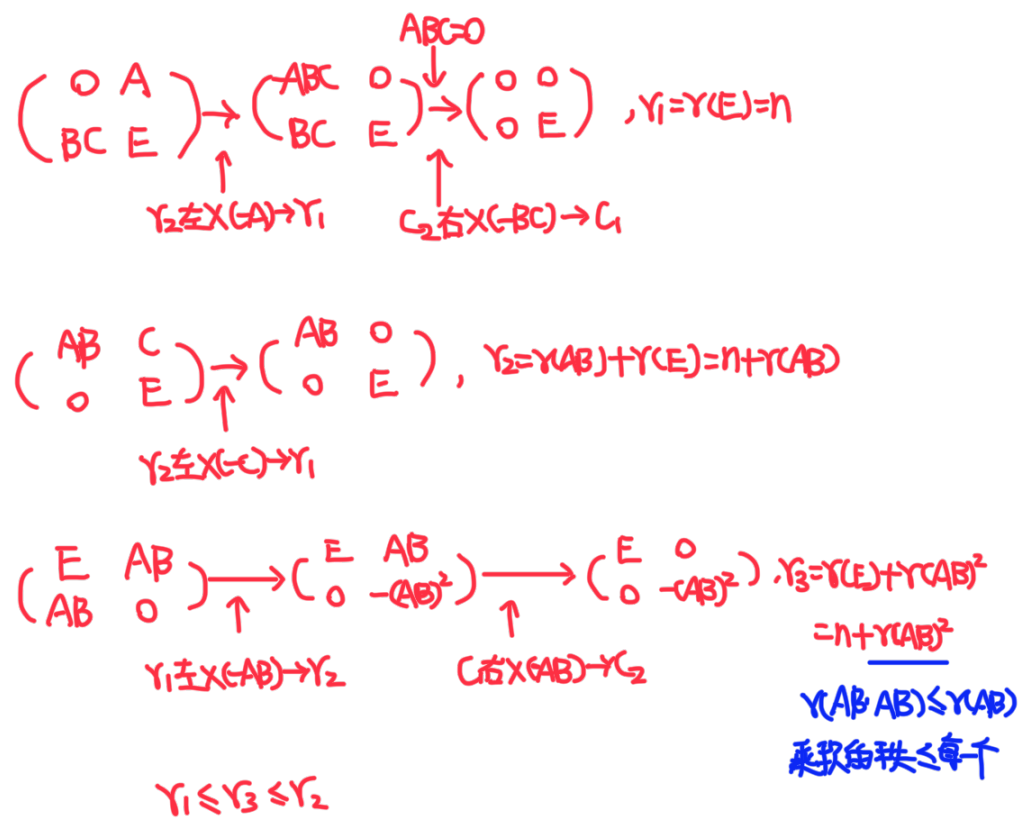
tag2,2

tag2，2
充分性找反例C=0

分块转置

tag2，0

tag2，0

分块矩阵秩

flag2，0

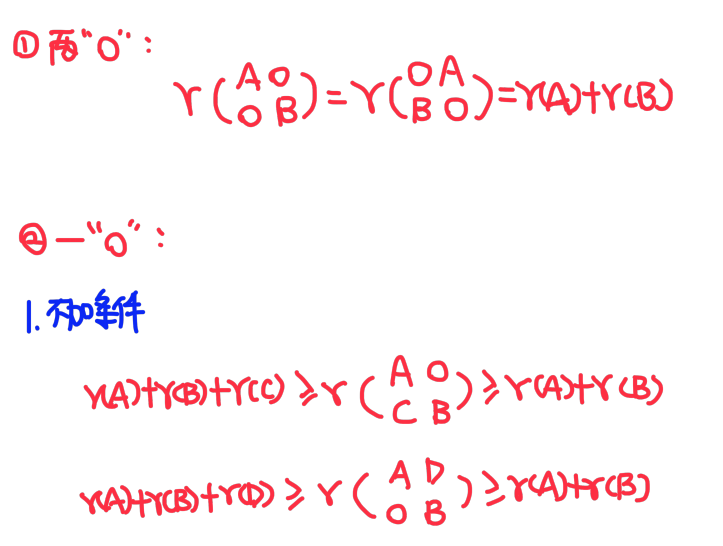
tag2，2

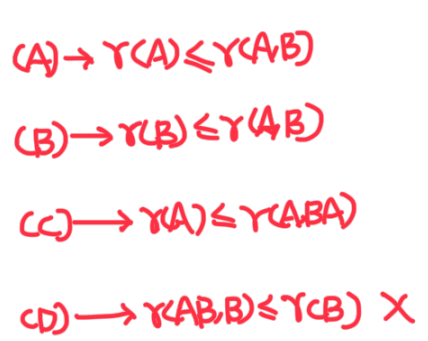
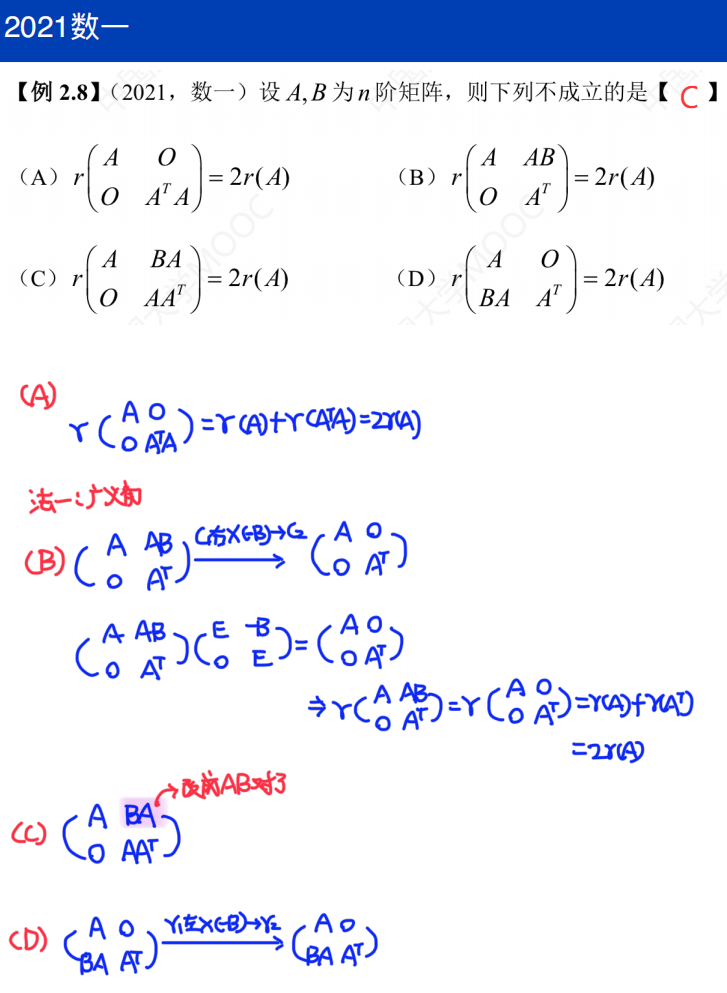
分块矩阵计算行列式

拆解后胖矩阵直接为0
tag2，0

AB=口

AB=E

tag2，0

tag2，0

AB=0

tag2，2

tag2，0


tag2，2
按照选项确定方向

AB=C

tag2，2

tag2

1. 矩阵等价：R(A) = R(B)
2. 向量组等价：R(A) = R(A | B) = R(B)

矩阵等价

求各⾏（列）元素之和

都可以从特征值和特征向量角度看
tag2，0

tag2，0
都可以从特征值和特征向量角度看

矩阵化E

行满秩

列满秩


只看ABC错哪了
tag2,0

tag2,0

矩阵分解

反对称矩阵

正交矩阵

这个类似于正交矩阵的处理手法要会！！！

向量（到这）

向量计算

tag3,0
!!!
正交化！！！！！！！！！！！！！！！！！！！！
tag

tag3，0

线性表示

线性表示的判定

B选项反例

只能行变换，因为这相当于是一个解方程

根据线性表示情况确定参数并将向量线性表示

（A | B） 再单独列一个 B 行变换，方便看秩

根据线性表示推理

---

以少表多，多必相关
无关被表，个数不多


取反例思考方向：

1. 取小矩阵，这样的排列组合少（2阶）
2. 若A，则B，找若A则！B
   
   
   
   

---

共同线性表示

向量组等价

秩/行列式求出初始的参数

线性相关无关

多个向量相关无关的关系

1. 矩阵拆分看秩
2. 定义
3. 充分条件
   
   
   
   
   
   证不出来应该先想反例（上面的题）
   
   
   
   分块矩阵右边系数与k无关
   
   
   部分和整体的关系
   低维和高维关系
   
   
   

根据相关⽆关确定参数

利用高维相关，低维一定相关的结论
求b同理


注：不能直接取一个四阶行列式里面的三阶子式，高维相关则低维相关的列数必须保持一致（若不一致相当于少了个元素，4个元素相关，3个元素完全可以无关）

证明无关（早年考的多，近年没考过）

极大无关组

行最简：每行第一个1的上下全为0
线性表示化为行最简
极大无关组用行阶梯就行


选做

选做

方程组

解的判定

判断解的情况

1. 利用秩（不等式）
2. 特征值
3. 行满秩，非齐次必定有解，列满秩不一定
   矩阵越拼越大，越乘越小
   tag4:wa
   
   
   | A | = 0，必定成立，否则就不可能无解
   
   主要看A、D
   看到这种秩为1的形式，想特征值
   tag4:
   
   
   正定矩阵有什么用？
   
   胖矩阵
   tag4:
   
   行满秩、列满秩结论
   对于C选项这里\(A^T\)是列满秩，而不是行满秩，增广矩阵的秩可能变动
   tag4：wa
   
   
   行满秩结论
   利用选择题的技巧：B、D最终导致的结果都是行满秩，因此应该一起排除
   行满秩，非齐次必定有解
   tag4
   

已知解的情况确定参数

1. 善用行列式为0，根据秩选择子式（（A | B)也可以选一个子式）
   B ！= 0，因此 AX=0，有非 0 解
   tag4
   
   
   
   

方程组求解

齐次

具体矩阵（重要题型）1

1. 给了一个具体矩阵，常常可以通过计算子式，确定秩的范围
   
   这样的矩阵分解为秩为1是通法
   tag4，0
   
   
   
   flag4，0
   
   \(a=-\frac{n(n+1)}{2}\) 时，用特征值来看基础解系
   tag4:wa
   
   把矩阵分解为秩为1
   
   
   
   tag4，2
   
   flag4，0
   第一问好好想想
   第三问看看就行
   
   
   
   

抽象矩阵

已知⼀个基础解系，证明另⼀个向量组为基础解系

1. 拆分矩阵
2. 左乘矩阵，构造齐次型
   拆矩阵
   
   
   tag4:
   
   tag4
   

已知若⼲⻬次解，判断其他向量是否为⻬次解

tag4:

1. 利用线性表示，列出一个矩阵
2. 抓住第二个解第二个位置为0，解方程
   

求基础解系中向量个数

tag4:

tag4:wa
对任意n维列向量a，有Aa=0,意思是基础解系有n个，而不是秩为n

tag4:

求基础解系（通解）1

区分基础解系和通解：通解是 k1、k2....... 倍基础解系
tag4，2

必做题，好题
flag4，0


tag4，0

到这-----------------------------------------------

好题


结合相似

AA*

必看题，好题





必做题，好题（AA*）

必做题，好题（AA*）

可以当一个结论：
\(\Large AA^* = |A|*E = 0,因此A可以为A^*提供齐次的解\)

非齐次

具体矩阵（补充）

好题

抽象矩阵

⾮⻬次⽅程组线性⽆关解向量的个数

已知解向量求通解

已知向量关系求通解

都是好题
通过把一个等式拆分成矩阵，凑齐次解手法学一下

已知解向量的线性组合求通解

系数和为0

重点

重点，处理手法牛逼

已知特征求通解

好题，最后判断非齐次特解直接代入即可

已知⼀⽅程组通解，求另⼀⽅程组通解

好题

好题

好题

根据其他已知条件求通解

好题



利用正交和自交的性质
正交必定可逆

解的关系

公共解(看看)

已知［I］［II］具体形式

flag2，00

已知［I］通解 ［II］具体形式

1. 通解代入已知方程
   flag2,00
   
   flag2,0
   
   

已知［I］［II］通解

flag2,0

同解

同解判断

tag2,0

反求参数

AX=0都是BX=0的解

矩阵方程

二阶

tag4，2
二阶的直接设出来

可逆

flag4，0

不可逆（到这）

不含参数直接解

第二问看作解三个非齐次的结果

tag4:

tag4

取转置的手法很有用
AB、BA 特征值特征向量转换

含参数讨论完解

其他情况

特征值和特征向量

求特征值特征向量

具体矩阵求特征值、特征向量

1. 特征值
   1. 行列式为0，必有一特征值为0
   2. 各行元素和相等则有全1的特征向量，特征值为倍数
   3. 迹
   4. 拆分为 aE + B，其中B为秩为 1 的矩阵
      动手化一下
      

拆分为秩为 1

A = B - E

各行元素和相等

转圈化简法

当前选中的元素只能消除他同行、同列的元素，顺时针一个个尝试

抽线矩阵求特征值、特征向量

jxq结论做一下
也可以一个个代入



\(b^Ta=0,取转置ab^T=0，解齐次方程组,a秩为1，两个基础解系，因此特征值有两个1\)

二次型

二次型的秩或矩阵

1. 平方和形式，写成\(B^TB\)，也可以求出秩\(r(B^TB)=r(B)\)
   1. 
      尽可能不要用行列式直接求，直接展开容易化简
      tag6
      
      换元的思想
      
      
      
      平方的和的形式才使用
      
      
      同样可以用平方的和来做\(\Large r(B^TB)=r(B)\)
      
      \(A=B^TB\)
      tag6
      
      
      
      

标准型

可逆变换x=Py

tag6
没咋了结论


tag6，0

正交变换x=Qy

1. 找特征值实在找不到了，想想特征值为0，求某个行列式为0或者秩不满
2. 正交变换后的矩阵相似且合同
3. 二次型矩阵概念
   1. 
      可以先通过B的特征向量求出A的特征向量，再去知一求二，构造出正交的B的向量
      求出(1,1,1)后用B第一列(-1,1,0)两者知二求一替换掉第二列
      tag6
      
      tag6
      通过正交变换得到的相似且合同
      

重要题型

注意A是一个正定矩阵

没咋了结论，做法要牢记
第一种和第二种都行

好题！！！
tag6
A 特征值记忆：出当前特征值以外特征值的乘积*
或者采用答案的方式求出A* 的对角矩阵

好题！！！
tag6
对特征值为0的要敏感
第一问可以用秩为1做

tag6
特别注意第一问
第一问证明用定义做
第二问是套路题

tag6
需要好好思考的题

1. 特向位置改变，A不变导致的结果是对角矩阵元素位置发生改变
2. 同一特征值的特向线性组合，仍然为特向，对应特征值不变
   
   
   tag6
   利用特征值，求行列式为0
   
   tag6
   难点在第一问
   
   相似、举例
   tag
   

给定矩阵不是实对称时

规范型

1. 正负特征值个数
2. 配方
3. 注意：判断规范型永远是以特征值为基准的，而不是形式
   
   特征值两负一正
   
   
   判断规范型永远是以特征值为基准的，而不是形式
   易错
   
   
   看个思路就行
   
   利用Q单位正交
   
   利用Q单位正交
   没咋了结论，答案是配方法，也可以采用第二种直接拆正定矩阵
   
   
   
   重要！！！
   求规范型利用正负特征值个数
   
   

正负惯性指数

1. 配方（保证是可逆变换才行）
2. 求特征值
3. 做多次可逆线性变换（能变的话）
   tag6
   韦达
   
   配方法保证可逆
   

自己构造可逆线性变换

不能用配方法，因为不可逆

tag6
做法


做两次可逆线性变换
tag6

好题，一定要完整的看
若做的不是可逆线性变化的话（直接看来），我们可以自己构造可逆线性变换化简，方便看正负特征值个数
tag6

其他

\(a^Ta>0\)
tag6

已知正负惯性指数信息确定参数或其他

tag6


tag6

tag6

合同

1. 合同唯一性质：正负惯性指数相同
2. 注意：实对称与实对称合同、非实对称和非实对称合同
   tag6
   易错
   
   
   
   tag6
   运用秩为1
   
   全部分解为秩为一
   tag6
   
   
   tag6
   
   tag6
   注意:\(aa^T\)
   

正定

已知正定 反求参数

1. 
   
   
   tag6
   没思路
   
   

⼀个⼆次型变成另⼀个⼆次型，求变换矩阵

1. 正交变换：利用相似，对角矩阵作为桥梁
2. 可逆线性变换：利用合同化为规范型（配方法），利用规范型唯一作为桥梁
3. 没咋了例题
4. 合同常常结合韦达定理，并且两个实对称合同秩相等

可逆变换

tag6

1. 也可以求特征值，其中B特征值不用算出来，因为是合同的，我们只要知道正负范围即可
   由韦达定理，知道B有2个负特征值，一个0特征值
   利用|A|=0，求出a
2. 两个实对称合同秩相等
   
   
   tag
   配方配错了
   
   
   
   tag6
   

正交变换

求⼆次型的解

1. 正交变换化为 \(y1^2+y2^2=0\) 只需满足\(y1=y2=0,y3任取(k_1)\) X=QY，Y=(0,0,k)
   1. 
2. 配方法，配出来\((x1+x2+x3)^2=0\)使得\(x1+x2+x3=0\) ，解齐次方程即可
   tag6
   T2忘记单位化
   
   tag6
   一定要动手做，第一问和第二问
   
   
   
   
   

求二次型最值

1. 首先正交变换化为标准型
2. 运用两个结论
   1. 
   2. 
      
      
      

求可逆阵 \(A = PP^T\)

1. 正定矩阵合同与E，找规范型
2. 拆分对角矩阵（根号）\(BQ^T\)
3. 
   
   
   
   
   
   tag
   第一问Q的性质