高斯-牛顿迭代

高斯牛顿迭代用于求解最小化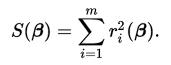（r中的函数数量大于等于β中的变量数量）

类似于牛顿迭代法寻找每一步迭代所得解得切线，高斯牛顿迭代法要找r在β处的最优线性逼近。

雅可比矩阵体现了一个可微方程与给出点的最优线性逼近，形式如下

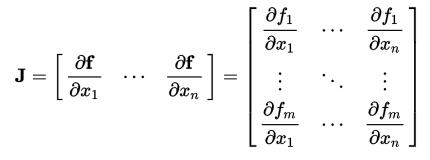
也就是说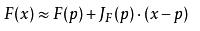

雅克比矩阵行数与列数不相等，所以求逆方法后结果为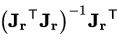。（这里也说明了r中的函数数量大于等于β中的变量数量的原因。如果不是则JrTJr不可逆）

于是每一次迭代的结果为

 

与牛顿迭代相同，高斯牛顿迭代的做法等同于忽略函数的二阶导。

忽略二阶导的条件为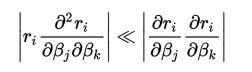。该条件满足有两种情况

1.ri较小2.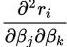较小，函数接近线性。

若二阶导不可忽略，函数不收敛

 

维基举例与实现代码。

设有n函数，m变量

单次迭代复杂度O(m^2*n)

#include <cstdio>
#include <cstring>
#include <cmath>
#include <iostream>
#define LDB long double
using namespace std;

 int n;
 LDB x[233],y[233],ans[233];

 struct matrix{
    LDB a[601][601],tmp[601][601];
    int n,m;
      
    void clear(){
      memset(a,0,sizeof(a));
      memset(tmp,0,sizeof(tmp));
    } 
      
    void cpy(matrix&b){
      n=b.n;m=b.m;
      for (int i=1;i<=n;i++)    
        for (int j=1;j<=m;j++)
          a[i][j]=b.a[i][j];
    }
      
    void mul(matrix &b){
      for (int i=0;i<=n;i++) 
        for (int j=0;j<=b.m;j++) 
          tmp[i][j]=0;
        
      for (int i=0;i<=n;i++)
        for (int k=0;k<=m;k++)
          if (a[i][k]){
              for (int j=0;j<=b.m;j++)
              tmp[i][j]+=a[i][k]*b.a[k][j];
            a[i][k]=0;
          }
      
      for (int i=0;i<=n;i++)
        for (int j=0;j<=b.m;j++)
          a[i][j]=tmp[i][j];
      m=b.m;
    }
    
    void getinv(){
      for (int i=1;i<=n;i++) for (int j=1;j<=n;j++) a[i][n+j]=0;
      for (int i=1;i<=n;i++) a[i][n+i]=1;
      for (int i=1;i<=n;i++){
        int po;LDB maxi=0;
        for (int j=i;j<=n;j++){
          if (fabs(a[j][i])>maxi){
            maxi=fabs(a[j][i]);po=j;
          }
        }
        for (int j=1;j<=2*n;j++){
          LDB t=a[i][j];a[i][j]=a[po][j];a[po][j]=t;
        }
        if (fabs(maxi)==0) continue;
            
        for (int j=i+1;j<=n;j++){
          LDB tim=a[j][i]/a[i][i];
          for (int k=i;k<=2*n;k++) a[j][k]-=a[i][k]*tim;
        }
      }
        
      for (int i=n;i>=1;i--){
        for (int j=i+1;j<=n;j++){
          for (int k=n+1;k<=2*n;k++)
            a[i][k]-=a[i][j]*a[j][k];
          a[i][j]=0;          
        }
        for (int j=n+1;j<=2*n;j++)
          a[i][j]/=a[i][i];
        a[i][i]=1;  
      }
      
      for (int i=1;i<=n;i++)
        for (int j=1;j<=n;j++)
          a[i][j]=a[i][j+n];
      for (int i=1;i<=n;i++) for (int j=1;j<=n;j++) a[i][j+n]=0;
    }
    
    void trav(){
      for (int i=1;i<=m;i++)
        for (int j=1;j<=n;j++)
          tmp[i][j]=a[j][i],a[j][i]=0;
      for (int i=1;i<=m;i++)
        for (int j=1;j<=n;j++)
          a[i][j]=tmp[i][j];
      swap(n,m);
    }
  }a,b,c,d;
  
  int main(){      
    scanf("%d",&n);
    for (int i=1;i<=n;i++) scanf("%Lf%Lf",&x[i],&y[i]);
    ans[1]=0.9;ans[2]=0.2;
    
    LDB tot=0;
    for (int i=1;i<=n;i++)
      tot+=(y[i]-ans[1]*x[i]/(ans[2]+x[i]))*(y[i]-ans[1]*x[i]/(ans[2]+x[i]));
    printf("0 %.6Lf %.6Lf %.6Lf\n",ans[1],ans[2],tot);
      
    for (int T=1;T<=10;T++){
      a.clear();b.clear();c.clear();d.clear();    
          
      a.n=n;a.m=2;
      for (int i=1;i<=n;i++)
        a.a[i][1]=-x[i]/(ans[2]+x[i]),
        a.a[i][2]=ans[1]*x[i]/(ans[2]+x[i])/(ans[2]+x[i]);
      b.cpy(a);c.cpy(a);
      d.n=n;d.m=1;
      for (int i=1;i<=n;i++)
        d.a[i][1]=y[i]-ans[1]*x[i]/(ans[2]+x[i]);
      a.trav();
      a.mul(b);
      a.getinv();
      c.trav();
      a.mul(c);
      a.mul(d);
      ans[1]=ans[1]-a.a[1][1];ans[2]=ans[2]-a.a[2][1];
      
      LDB tot=0;
      for (int i=1;i<=n;i++)
        tot+=(y[i]-ans[1]*x[i]/(ans[2]+x[i]))*(y[i]-ans[1]*x[i]/(ans[2]+x[i]));
      printf("%d %.6Lf %.6Lf %.6Lf\n",T,ans[1],ans[2],tot);
    }
  }