【总结】并查集

并查集

• 并查集，用于处理一些不交集的合并及查询问题。
• 可以支持以下操作
  • 建立集合
  • 查找祖先
  • 合并集合

建立并查集

没有什么好说的，对于每一个节点，一开始自己是一个独立的集合。

const int MAXN = 1e5 + 5;
int fa[MAXN];
void Make() {
	for (int i = 1; i <= n; i++)
		fa[i] = i;
}

查找祖先

对于每个节点，我们都知道它的父亲节点，所以，我们可以沿着父亲节点，一直往上爬，就可以找到祖先。

那我们则么知道谁是祖先？通过上面的初始化我们可以知道，对于每一个祖先都满足 \(fa_i = i\)，可以通过父亲节点一个一个向上找。

我们就可以写出代码

int Find(int x) {
	return fa[x] == x ? x : Find(fa[x]);
}

合并集合

对于两个集合 \(X\) 和 \(Y\)，我们只需要让某个集合的一个元素存在于另一个集合当中，我们就可以合并两个集合。

那么，对于并查集而言，我们只需将其中一个集合的祖先的父亲设为另一个集合的祖父即可。

void Union(int x, int y) {
	x = Find(x), y = Find(y);
	if (x != y)
		fa[x] = y;
}

查询的优化

我们可以看看这张图

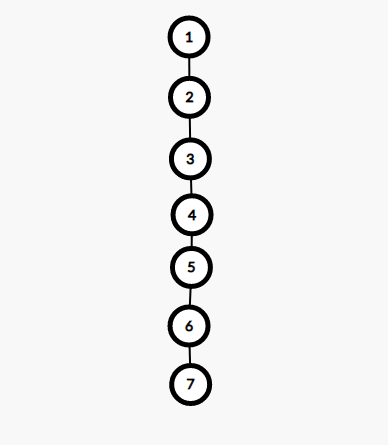
如果我们要查找 \(7\) 的祖先，速度就会非常慢。

所以我们就要采用优化 —— 路径压缩。

我们不需要知道并查集具体的样子，只需要知道它的祖先是谁，所以我们可以得到一个等价的并查集。

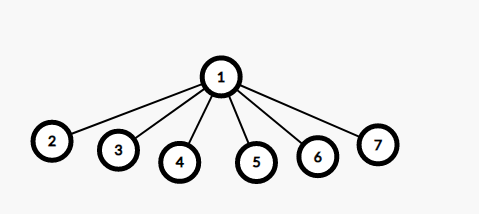
我们在查询时，只需要把它的父亲节点直接更改为祖先，当下一次查询时，只需要一次就可以找到祖先，在优化查询时，合并由于也需要查找，所以合并也得到了有优化。

int Find(int x) {
	return fa[x] == x ? x : fa[x] = Find(fa[x]);
}

在优化查询时，合并也会得到一定的优化。

合并的优化

其实一般的题，路径压缩已经够用了，

但是有些毒瘤不会放过你，所以我们必须使用按秩式合并。

我们首先考虑合并一下两个集合。

我们有两种方式合并它们

• 

• 

很显然第一种更优，即把深度较小的集合合并深度较大的集合里面。

可以定义一个 \(rank\) 数组表示节点深度。

void Union(int x, int y){
	int fax = Find(x), fay = Find(y);
	if (fax == fay)
		return ;
	if (rank[fax] <= rank[fay])
		fa[fax] = fay;
	else
		fa[fay] = fax;
	if (rank[fax] == rank[fay])
		rank[fay]++;
}

例题

基本并查集

• 亲戚
  这就是一道模板题，没有什么好讲的，直接看代码吧。

#include <iostream>
#include <cstdio>
using namespace std;
const int MAXN = 20005;
int n, m, q;
int fa[MAXN], rank[MAXN];
void Make() {
	for (int i = 1; i <= n; i++)
		fa[i] = i, rank[i] = 1;
}
int Find(int x) {
	return fa[x] == x ? x : fa[x] = Find(fa[x]);
}
void Union(int x, int y){
	int fax = Find(x), fay = Find(y);
	if (fax == fay)
		return ;
	if (rank[fax] <= rank[fay])
		fa[fax] = fay;
	else
		fa[fay] = fax;
	if (rank[fax] == rank[fay])
		rank[fay]++;
}
int main() {
	scanf("%d %d", &n, &m);
	Make();
	for (int i = 1; i <= m; i++) {
		int x, y;
		scanf("%d %d", &x, &y);
		Union(x, y);
	}
	scanf("%d", &q);
	for (int i = 1; i <= q; i++) {
		int x, y;
		scanf("%d %d", &x, &y);
		if (Find(x) == Find(y))
			printf("Yes\n");
		else
			printf("No\n");
	}
	return 0;
}

带权并查集

• 银河英雄传说
  我们可以添加一个 \(d\) 数组，用于维护它们的深度。

若我们想要知道 \(x\) 与 \(y\) 之间有多少艘战舰，只需要求得它们的深度差在 -1。
即 \(ans = abs(d_x - d_y) - 1\)。

所以我们应该考虑如何去维护 \(d\) 数组。

若我们将 \(x\) 并到 \(y\) 上，那么 \(d_x += size_y\)，因为它是一条链。

我们就可以得到以下代码

void Union(int x, int y){
	x = Find(x), y = Find(y);
	if (x != y) {
		fa[x] = y, d[x] = size[y], size[y] += size[x];
	}
}

当然不可能有这么简单

我们考虑如何更新 \(d_x\)。对于任意一点的 \(x\), \(d_x = d_x + d_{fa_x}\)

所以我们可以修改 Find。

int Find(int x) {
	if (fa[x] == x)
		return x;
	int root = Find(fa[x]);
    d[x] += d[fa[x]];
	return fa[x] = root;
}

完整代码如下

#include <cstdio>
const int MAXN = 30005;
int n;
int fa[MAXN], d[MAXN], size[MAXN];
void Make() {
	for (int i = 1; i <= 30000; i++)
		fa[i] = i, size[i] = 1;
}
int Find(int x) {
	if (fa[x] == x)
		return x;
	int root = Find(fa[x]);
    d[x] += d[fa[x]];
	return fa[x] = root;
}
void Union(int x, int y){
	x = Find(x), y = Find(y);
	if (x != y) {
		fa[x] = y, d[x] = size[y], size[y] += size[x];
	}
}
int Abs(int x) {
	return x > 0 ? x : -x;
}
int main() {
	scanf("%d", &n);
	Make();
	for (int i = 1; i <= n; i++) {
		char op[5];
		int x, y;
		scanf("\n%s %d %d", op + 1, &x, &y);
		if (op[1] == 'M') {
			Union(x, y);
		} else {
			if (Find(x) != Find(y))
				printf("-1\n");
			else
				printf("%d\n", Abs(d[x] - d[y]) - 1);
		}
	}
	return 0;
}

扩展域并查集

• 团伙

#include <cstdio>
const int MAXN = 1e3 + 5;
int n, m, ans;
int fa[MAXN * 2];
void Make() {
	for (int i = 1; i <= 2 * n; i++)
		fa[i] = i;
}
int Find(int x) {
	return fa[x] == x ? x : fa[x] = Find(fa[x]);
}
void Union(int x, int y){
	fa[Find(x)] = Find(y);
}
int main() {
	scanf("%d %d", &n, &m);
	Make();
	for (int i = 1; i <= m; i++) {
		int op, x, y;
		scanf("%d %d %d", &op, &x, &y);
		if (op == 0)
			fa[Find(x)] = Find(y);
		else {
			Union(x + n, y);
			Union(y + n, x);
		}
	}
	for (int i = 1; i <= n; i++)
		if (i == fa[i])
			ans++;
	printf("%d", ans);
	return 0;
}